Требование к оформлению контрольных и расчетно-графических работ
ЗАДАНИЯ для КОНТРОЛЬНОЙ РАБОТЫ
По ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
для ПГС – 15 з (3,5)
Требование к оформлению контрольных и расчетно-графических работ
Контрольные и расчетно-графические работы выполняются на листах формата А4 согласно общих требований к оформлению текстовых документов. Допускается выполнение работы на листах в клетку (А4). Данные условий задач переписывать обязательно, рисунки к задачам выполнять четко в соответствии с требованиями начертательной геометрии и инженерной графики.
Преобразование формул, уравнений в ходе решение производить в общем виде, а затем подставлять исходные данные. Порядок подстановки числовых значений должен соответствовать порядку расположения в формуле буквенных обозначений этих величин. После подстановки исходных значений вычислить окончательный или промежуточный результат.
При решении применять международную систему единиц (СИ), а также кратные и дольные от них. Для обозначения основных общетехнических величин использовать только стандартные символы (обозначения).
Тщательно проверить правильность всех вычислений, обратив особое внимание на соблюдение правильности размерности, подставляемых в формулу значений, оценить правдоподобность полученного результата.
Таблица с номерами вариантов
| № варианта | ||||
| Абрамов | Андрей | Александрович | ||
| Ахмашева | Любовь | Анатольевна | ||
| Гилевский | Федор | Владимирович | ||
| Горбунов | Павел | Владимирович | ||
| Гришина | Юлия | Александровна | ||
| Калиев | Любомир | Робертович | ||
| Кирьянова | Яна | Дмитриевна | ||
| Копцева | Кристина | Владиславовна | ||
| Коршунов | Алексей | Львович | ||
| Курочкина | Наталья | Васильевна | ||
| Миков | Владислав | Александрович | ||
| Овчинников | Сергей | Анатольевич | ||
| Пушкарный | Роман | Анатольевич | ||
| Сайфуллин | Александр | Александрович | ||
| Ташкинов | Александр | Николаевич | ||
| Тепляков | Вадим | Андреевич | ||
| Толмачев | Алексей | Михайлович | ||
| Туз | Виктор | Викторович | ||
| Тюлянкин | Максим | Юрьевич | ||
| Хамитов | Руслан | Загитович | ||
| Цигвинцев | Юрий | Владимирович | ||
| Шамшурин | Кирилл | Анатольевич | ||
| Шилов | Юрий | Александрович |
Контрольная работа состоит из семи задач (С1-С7)
Указания к задаче С1-С4(выполняются по одному рисунку).
Номер рисунка конструкции соответствует номеру вашего варианта, указанного выше, необходимые данные для расчета приведены в таблице С1.
Первое комплексное задание на темы «Произвольная плоская система сил» и «Центр тяжести». Прежде чем приступить к выполнению этих заданий, необходимо изучить следующие разделы статики:
1. Основные положения и аксиомы статики.
2. Сходящиеся силы.
3. Теория пар на плоскости.
4. Произвольная плоская система сил.
5. Центр тяжести плоской фигуры.
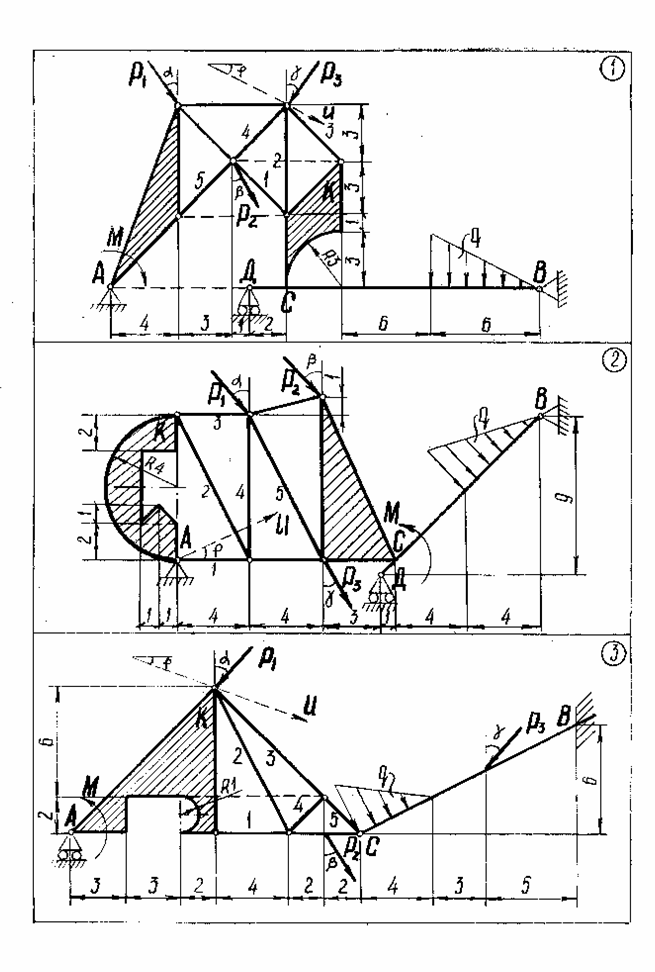
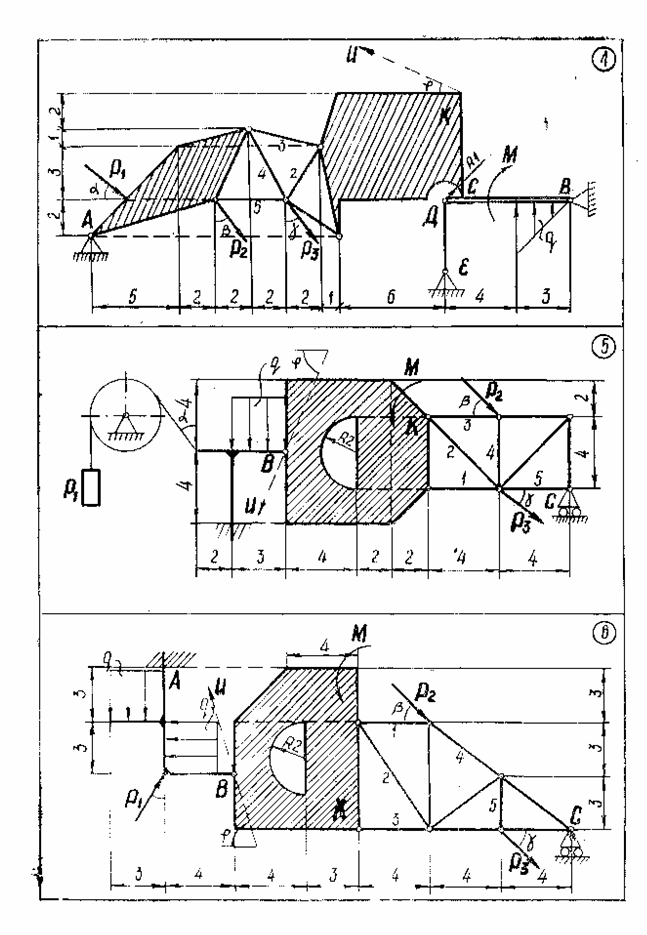
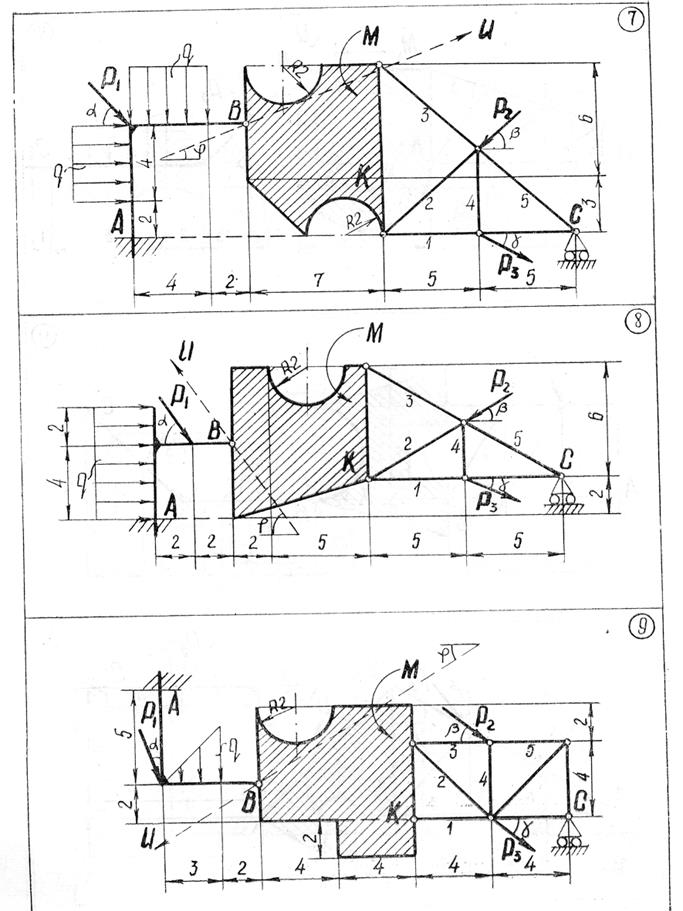
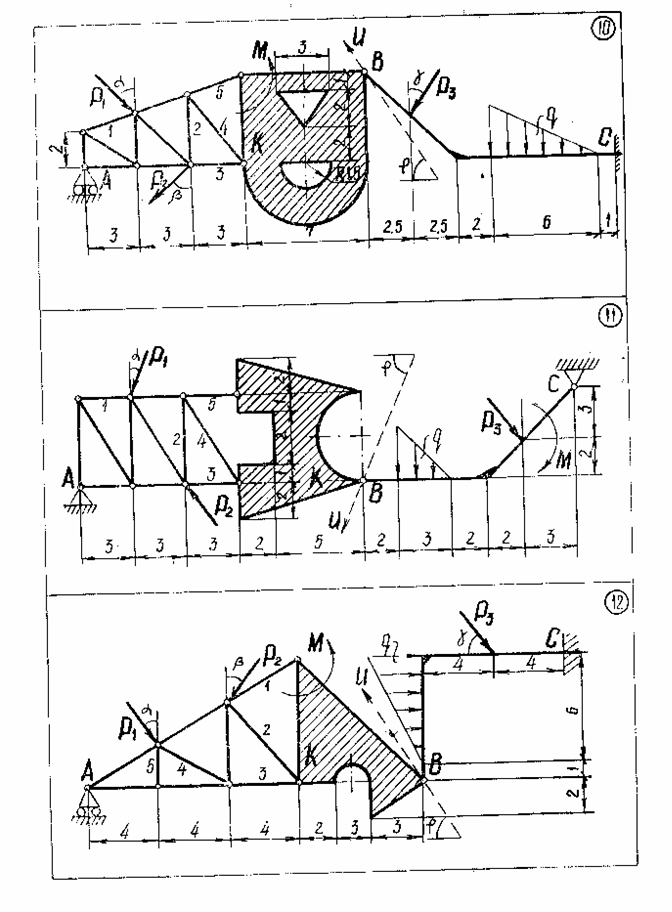
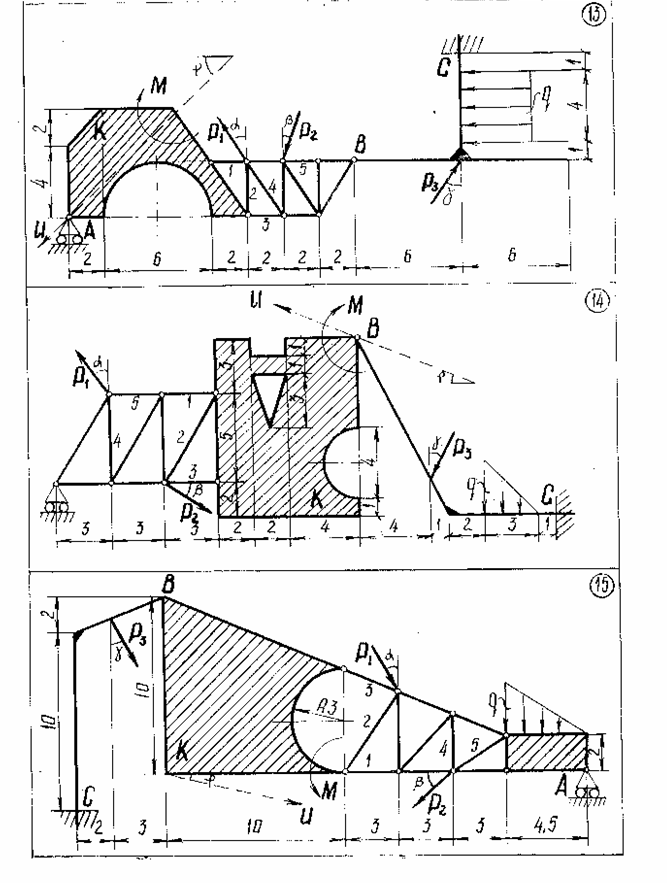
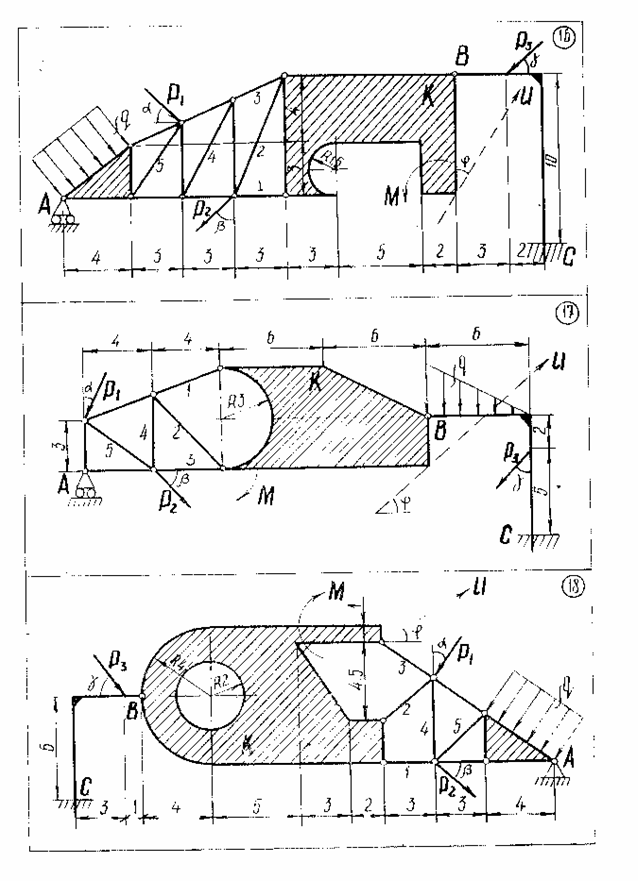
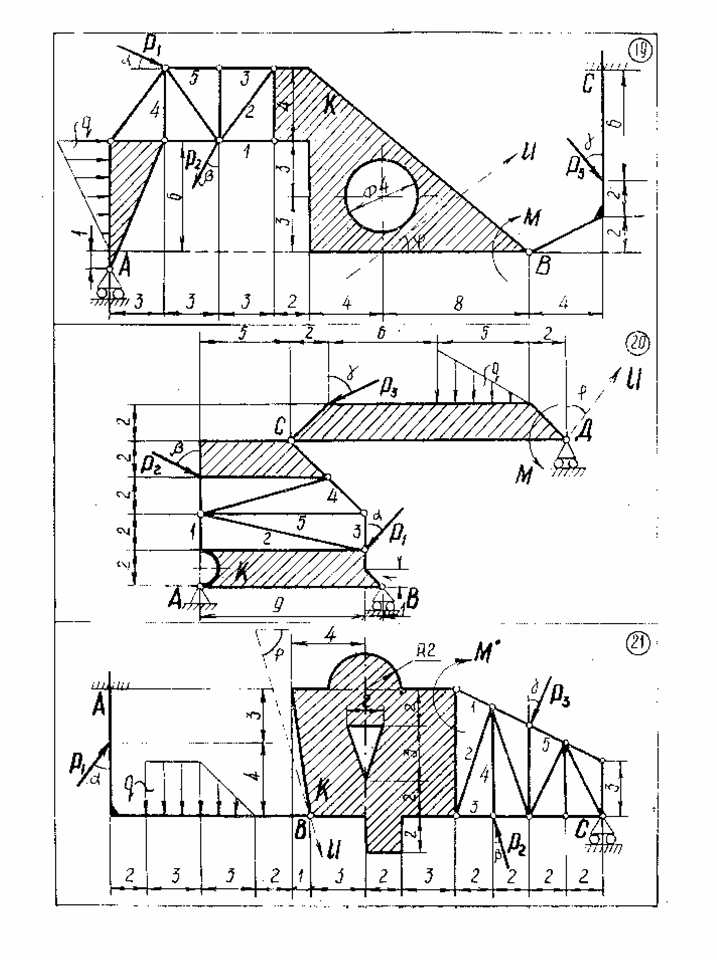
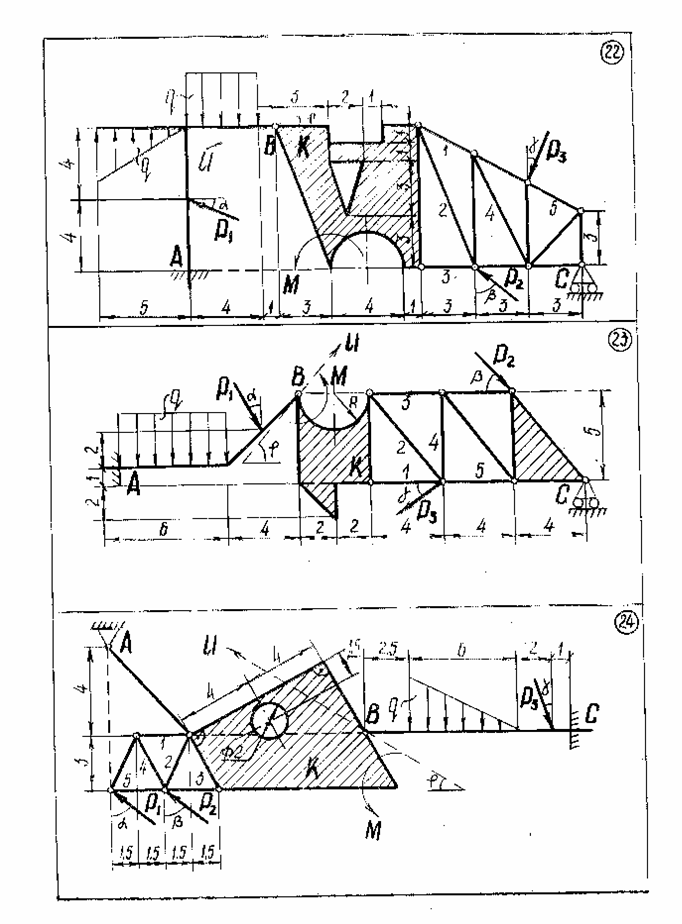
Задание С1-С5.Заданная система сил состоит из трех сосредоточенных сил 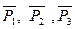 распределенной нагрузки заданной интенсивность q и пары сил с данным моментом m.
распределенной нагрузки заданной интенсивность q и пары сил с данным моментом m.
Задание состоит из следующих разделов:
С1. Пользуясь методом Пуансо, привести систему сил к центру, принимая за центр приведения: Точку А; Точку С. (С этой целью следует найти главный вектор данной системы сил и главный моменты системы относительно точек А и С). Проверить сделанные в пунктах 1 и 2 вычисления, применяя формулу изменения главного момента при изменении центра приведения.
С2. Рассматривая конструкцию как одно тело, воспользоваться аксиомой связей и дать схему сил, действующую на всю систему в целом. Расчленить конструкцию на две части (в вариантах №№ 1, 2, 4 одна часть конструкции свободно опирается на другую в точке С; в вариантах №№ 3, 20, 30, 31, 32, 51, 54, обе части конструкции скреплены шарниром С; в вариантах №№ 28, 29 – шарниром Е; в варианте №44 – шарниром Е и невесомым стержнем СД; в остальных - шарниром В). Пользуясь полученными схемами сил, найти реакции связей.
С3. Найти усилия в стержнях 1, 2, 3, 4, 5 методом Риттера. Для проверки полученных в пунктах II, III результатов рассмотреть равновесие тела К, составив сумму проекций на ось проверки U всех действующих на тело К сил (чертеж тела К со схемой действующих на него сил должен быть дан).
С4.Выбрав координатные оси, найти центр тяжести плоской фигуры К.
Таблица С1 (к задаче 1)
| №№ варианта | Р1 | Р2 | Р3 | m | q | α | β | γ | φ | ||
| кН | кН | кН | кН·м | кН/м | град | град | град | град | |||
| 1,5 | |||||||||||
| 0,5 | |||||||||||
| 1,5 | |||||||||||
| 0,5 | |||||||||||
| 0,5 | |||||||||||
| 0,5 | |||||||||||
| 1/5 | |||||||||||
| 0?5 | |||||||||||
| 1?5 | |||||||||||
Указания к задачам С5, С6 и С7.К задачам 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С2.3 - это рис. 3 к задаче С2 и т.д. Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы.
Студент в задачах С5, С6, С7 выбирает номер рисунка по первой цифре варианта, а номер условия в таблице - по последней; например, если № варианта оканчивается числом 46, то берет рис. 4 и условия № 6 из таблиц, если номер варианта 3, то берется рисунок 0, и условие №3.
Задача С5
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам A, B, C, D (рис. С5.0 – С5.9, табл. С5). Стержни и узлы (узлы расположены в вершинах H, K, L или М прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила Р=200 Н; во втором узле приложена сила Q=100 H. Сила 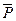 образует с положительными направлениями координатных осей x, y, z углы, равные соответственно α1=450, β1=600, γ=600, а сила
образует с положительными направлениями координатных осей x, y, z углы, равные соответственно α1=450, β1=600, γ=600, а сила 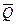 - углы α2=600, β2=450, γ2=600; направления осей x, y, z для всех рисунков показаны на рис. С2.0.
- углы α2=600, β2=450, γ2=600; направления осей x, y, z для всех рисунков показаны на рис. С2.0.
Грани параллелепипеда, параллельные плоскости xy, - квадраты. Диагонали других боковых граней образуют с плоскостью xy угол φ=600, а диагональ параллелепипеда образуют с плоскостью угол θ=510. Определить усилия в стержнях.
На рис. С5.10 в качестве примера показано, как должен выглядеть чертёж С5.1, если по условиям задачи узлы находятся в точках L и М, а стержнями являются LM, LA, LB, MA, MC, MD.Там же показаны углы φ и θ; при решении своей задачи на рисунке следует указать заданные значения этих углов.
Указания. Задача С2 – на равновесие пространственной системы, сходящихся сил. При её решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходится три стержня.
Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, 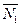 ,
, 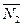 и т.д.).
и т.д.).
Таблица С5
| Номер условия | |||||
| Узлы | H, M | L, M | K, M | L, H | K, H |
| Стержни | HM, HA, HB, MA, MC, MD. | LM, LA, LD, MA, MB, MC. | KM, KA, KB, MA, MC, MD. | LH, LC, LD, HA, HB, HC. | KH, KB, KC, HA, HC, HD. |
| Номер условия | |||||
| Узлы | M, H | L, H | K, H | L,M | K,M |
| Стержни | MH, MB, MC, HA, HC, HD. | LH, LB, LD, HA, HB, HC. | KH, KC, KD, HA, НB, НC. | LM, LB, LD, MA, MB, MC. | KM, KA, KD, MA, MB, MC. |
Пример С5.Конструкция состоит из несовместимых стержней 1, 2, …6, соединенных друг с другом (в узлах K и М) и с неподвижными опорами A, B, C, D шарнирами (рис. С2). В узлах К и М приложены силы 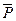 и
и 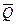 , образующие с координатными осями углы α1, β1, γ1, и α2, β2, γ2 соответственно (на рисунке показаны только углы α1, β1, γ1).
, образующие с координатными осями углы α1, β1, γ1, и α2, β2, γ2 соответственно (на рисунке показаны только углы α1, β1, γ1).
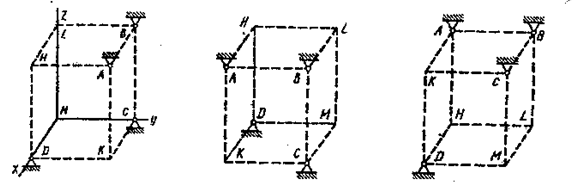
Рис.5.0 Рис. 5.1 Рис.5.2
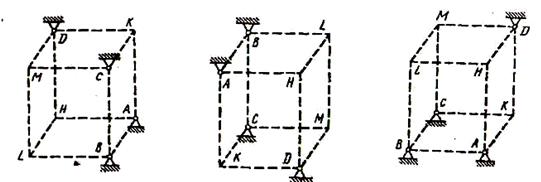
Рис.5.3 Рис. 5.4 Рис.5.5
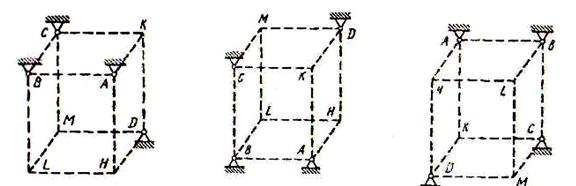
Рис.5.6 Рис. 5.7 Рис.5.8
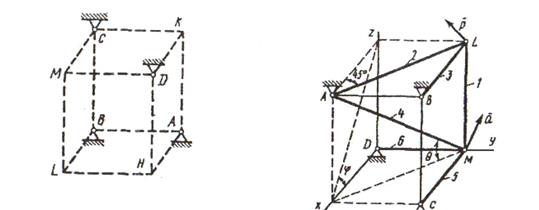
Рис.5.9 Рис.5.10
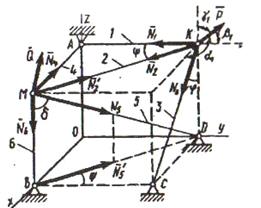 Дано: P=100 H, α1=60, Q=50 H, α2=450,
Дано: P=100 H, α1=60, Q=50 H, α2=450,
β2=600, γ2=600, ψ=300, φ=600, δ=740;
Определить: Усилия в стержнях 1-6.
Решение. 1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. На узел действуют:
а) активная сила 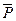
б) реакции связей (стержней): 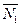 ,
, 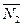 ,
, 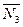 , которые направим по стержням от узла, считая стержни растянутыми. Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:
, которые направим по стержням от узла, считая стержни растянутыми. Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:
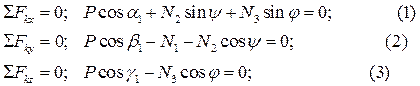
Решив уравнения (1), (2), (3) при заданных числовых значениях силы Р и углов, получим N1=349 Н, N2=-345 H, N3=141 H.
2. Рассмотрим равновесие узла М. На узел действуют:
а) активная сила 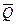 ;
;
б) реакции связей (стержней) 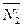 ,
, 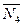 ,
, 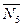 ,
, 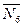 . При этом по закону о равенстве действия и противодействия реакция
. При этом по закону о равенстве действия и противодействия реакция 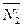 направлена противоположно
направлена противоположно 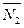 , численно же
, численно же 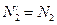 . Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:
. Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:
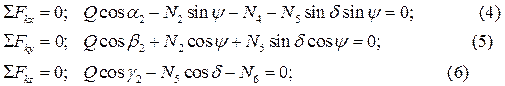
При определении проекций силы 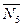 на оси Оx и Оy в уравнениях (4) и (5) удобнее сначала найти проекцию
на оси Оx и Оy в уравнениях (4) и (5) удобнее сначала найти проекцию 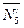 этой силы на плоскость xОy (по числовой величине
этой силы на плоскость xОy (по числовой величине 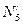 =N5 sinδ), а затем найденную проекцию на плоскость спроектировать на оси Ox, Oy.
=N5 sinδ), а затем найденную проекцию на плоскость спроектировать на оси Ox, Oy.
Решив систему уравнений (4), (5), (6) и учитывая, что 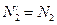 =-345 H, найдём чему равны N4, N5, N6. Напоминаем, что в своей задаче решение систем уравнений (1)-(3) и (4)-(6) следует выполнить подробно и с пояснениями.
=-345 H, найдём чему равны N4, N5, N6. Напоминаем, что в своей задаче решение систем уравнений (1)-(3) и (4)-(6) следует выполнить подробно и с пояснениями.
После решения сделайте проверку, составив для любого узла уравнение 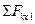 , где ось x1 направьте, например, по диагонали квадрата, расположенного в плоскости xOy. Эта сумма должна получиться равной нулю.
, где ось x1 направьте, например, по диагонали квадрата, расположенного в плоскости xOy. Эта сумма должна получиться равной нулю.
Ответ: N1=349 H; N2= - 345 H; N3=141 H; N4=50 H; N5=329 H; N6=-66 H. Знаки показывают, что стержни 2 и 6 сжаты, остальные - растянуты.
Задача С6
Однородная прямоугольная плита весом 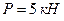 со сторонами
со сторонами 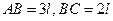 закреплена в точке А сферическим шарниром, а в точке B цилиндрическим шарниром (подшипником) и держится в равновесии невесомым стержнем СС/ (рис. С6.0-С6.9).
закреплена в точке А сферическим шарниром, а в точке B цилиндрическим шарниром (подшипником) и держится в равновесии невесомым стержнем СС/ (рис. С6.0-С6.9).
На плиту действует пара сил с моментом М=6 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С6; при этом силы 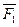 и
и 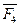 лежат в плоскостях, параллельных плоскости хОу, сила
лежат в плоскостях, параллельных плоскости хОу, сила 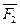 - в плоскости, параллельной
- в плоскости, параллельной 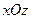 , сила
, сила 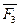 - в плоскости, параллельной уОz. Точки приложения сил (D, Е, H) находятся в серединах сторон плиты. Укажите на рисунке численные значения всех углов.
- в плоскости, параллельной уОz. Точки приложения сил (D, Е, H) находятся в серединах сторон плиты. Укажите на рисунке численные значения всех углов.
Определить реакции связей в точках А, В и С. При подсчетах принять l=0,8 м.
Указания. Задача С6 - на равновесие пространственной системы произвольно расположенных сил. Для ее решения необходимо заменить действие связей реакциями и составить шесть уравнений равновесия: суммы проекций всех сил на оси х, у, z и суммы моментов всех сил относительно осей х, у, z.
Таблица С6
| Сила | 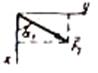 | 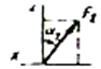  | 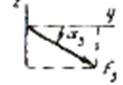 | 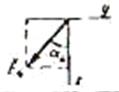 | ||||
| Номер условия | F1=4 кН | F2=6 кН | F3=8 кН | F4=10 кН | ||||
| Точка прило-жения | 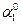 | Точка прило-жения | 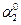 | Точка прило-жения | 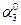 | Точка прило-жения | 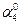 | |
| D | - | - | E | - | - | |||
| H | D | - | - | - | - | |||
| - | - | E | - | - | D | |||
| - | - | - | - | E | H | |||
| E | - | - | H | - | - | |||
| - | - | D | Н | - | - | |||
| - | - | H | - | - | D | |||
| E | H | - | - | - | - | |||
| - | - | - | - | D | E | |||
| - | - | E | D | - | - |
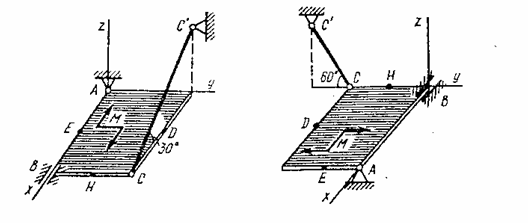
Рис. С6.0 Рис. С6.1
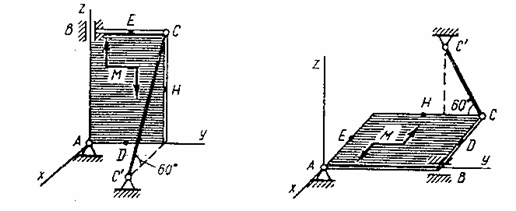
Рис. С6.2 Рис. С6.3
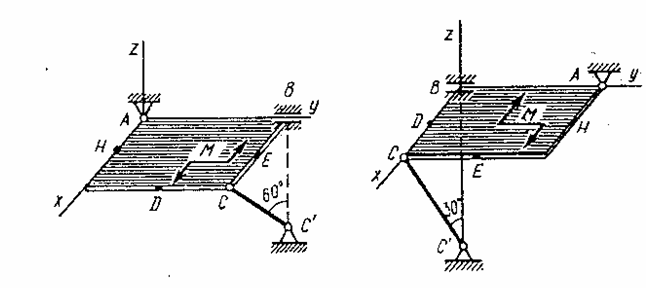
Рис. С6.4 Рис. С6.5
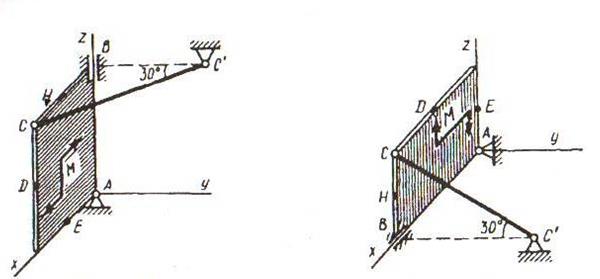
Рис.6.6 Рис.6.7
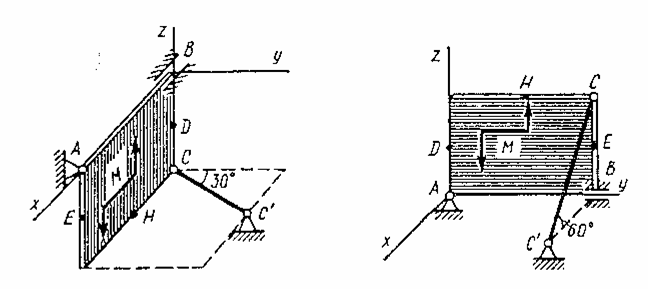
Рис. С6.8 Рис. С6.9
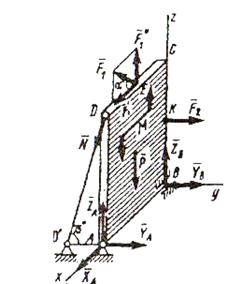 Пример C6. Вертикальная прямоугольная плита весом P (рис. C6) закреплена сферическим шарниром в точке A, цилиндрическим (подшипником) в точке B и невесомым стержнем DD/, лежащим в плоскости, параллельной плоскости yz. На плиту действует сила
Пример C6. Вертикальная прямоугольная плита весом P (рис. C6) закреплена сферическим шарниром в точке A, цилиндрическим (подшипником) в точке B и невесомым стержнем DD/, лежащим в плоскости, параллельной плоскости yz. На плиту действует сила 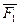 (в плоскости xz) и пара сил с моментом M (в плоскости плиты).
(в плоскости xz) и пара сил с моментом M (в плоскости плиты).
Дано: P= 5 кН, М= 3 кН 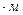 , F
, F 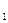 = 6 кН, F
= 6 кН, F 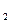 = 7,5 кН,
= 7,5 кН, 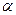 = 30
= 30  , AB = 1 м, BC= 2 м, CE= 0,5 AB. BK= 0,5 BC.
, AB = 1 м, BC= 2 м, CE= 0,5 AB. BK= 0,5 BC.
Определить: реакции опор A, B и стержня DD/.
Решение. Рассмотрим равновесие плиты. На неё действуют:
а) активные силы 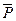 ,
, 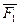 ,
, 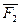 и пара сил, момент которой М;
и пара сил, момент которой М;
б) реакции связей: реакцию сферического шарнира A разложим на три составляющие 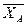 ,
, 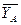 ,
, 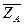 , цилиндрического шарнира (подшипника) B – на две составляющие
, цилиндрического шарнира (подшипника) B – на две составляющие 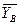 ,
, 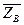 (в плоскости, перпендикулярной оси подшипника), реакцию
(в плоскости, перпендикулярной оси подшипника), реакцию 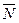 стержня направим вдоль стержня, предполагая, что он растянут.
стержня направим вдоль стержня, предполагая, что он растянут.
Силы, приложенные к плите, образуют пространственную систему сил.
Составляем уравнения её равновесия:
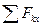 = 0, X
= 0, X 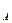 + F
+ F 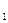 cos 30
cos 30  = 0, (1)
= 0, (1)
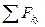 = 0, Y
= 0, Y 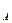 + Y
+ Y 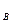 +F
+F 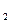 - N cos 75
- N cos 75  = 0, (2)
= 0, (2)
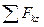 = 0, Z
= 0, Z 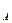 + Z
+ Z 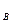 - P – N sin 75
- P – N sin 75  + F
+ F 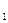 sin 30
sin 30  = 0, (3)
= 0, (3)
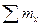 (
( 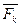 ) = 0, - F
) = 0, - F 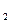
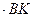 + N cos 75
+ N cos 75 
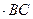 = 0, (4)
= 0, (4)
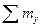 (
( 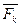 ) = 0, P
) = 0, P 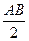 + F
+ F 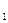 cos 30
cos 30 
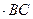 - F
- F 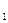 sin 30
sin 30 
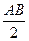 - Z
- Z 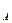
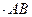 +
+
+N sin 75 
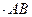 + M = 0, (5)
+ M = 0, (5)
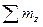 (
( 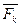 ) = 0, Y
) = 0, Y 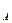
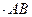 - N cos 75
- N cos 75 
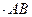 = 0. (6)
= 0. (6)
Для определения момента силы 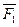 относительно оси у раскладываем
относительно оси у раскладываем 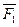 на составляющие
на составляющие 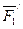 и
и 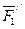 , параллельные осям х и z (
, параллельные осям х и z ( 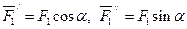 ), и применим теорему Вариньона (относительно оси). Аналогично можно поступить при определении моментов реакции
), и применим теорему Вариньона (относительно оси). Аналогично можно поступить при определении моментов реакции 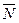 .
.
Подставив в уравнения (1)-(6) числовые значения заданных величин и решив эти уравнения, найдем величины реакций связей.
В своей задаче систему уравнений (1)-(6) следует решить полностью и с пояснениями. Сделайте проверку, например, составив уравнение моментов относительно оси х1, проведенной параллельно оси х.
Ответ: ХА =-5,2 кH; YА= 3,8 кH; ZА=28,4 кН; YВ=-7,5 к H; ZВ=-12,4 кH; N6=14,5 кH.
Знаки показывают, что силы 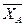 ,
, 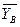 и
и 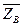 направлены противоположно показанным на рис. С6.
направлены противоположно показанным на рис. С6.
Задача С7
Однородные брусья AC весом P 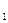 = 15 H и BD (или BC) весом P
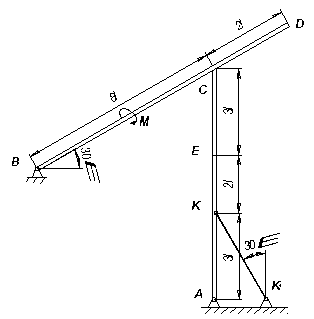
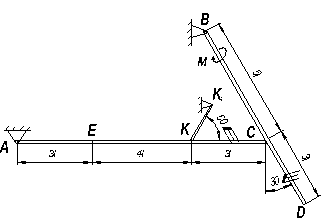
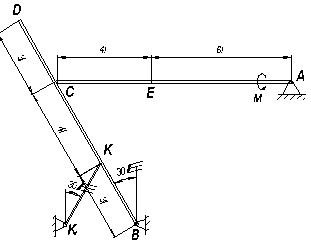
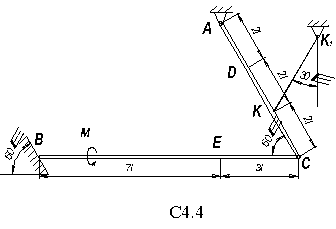
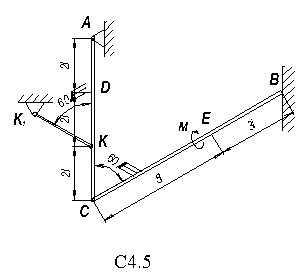
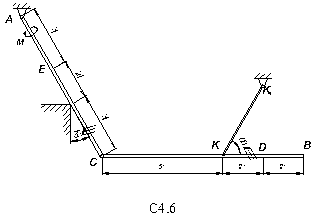
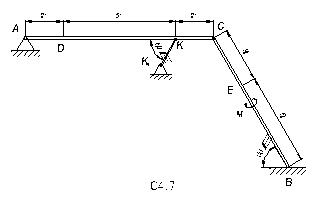
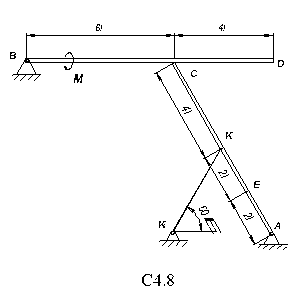
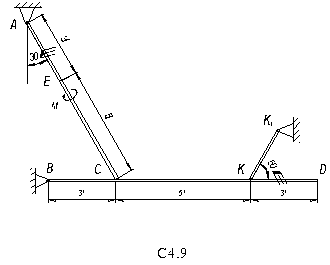
= 15 H и BD (или BC) весом P 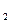 = 25 H расположены в вертикальной плоскости (рис. С7.0 – C7.9, табл. С7). В точке C брусья или свободно опираются друг о друга (рис. 0 – 5), или соединены шарниром (рис. 6 – 9). Внешними связями являются шарнир в точке А, невесомый стержень КК
= 25 H расположены в вертикальной плоскости (рис. С7.0 – C7.9, табл. С7). В точке C брусья или свободно опираются друг о друга (рис. 0 – 5), или соединены шарниром (рис. 6 – 9). Внешними связями являются шарнир в точке А, невесомый стержень КК 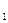 , шарнир в точке B (на рис. 0 – 5), выступ H (на рис. 6) и гладкая плоскость (на рис. 7 – 9 в точке B).
, шарнир в точке B (на рис. 0 – 5), выступ H (на рис. 6) и гладкая плоскость (на рис. 7 – 9 в точке B).
На брусья кроме сил тяжести действуют пара сил с моментом M = 50 Hм и сила, величина которой, направление и точка приложения указаны в табл. С4 (например, по условиям № 1 таблицы на брус действует сила F 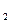 = 20 H, приложенная в точке Е и направленная под углом
= 20 H, приложенная в точке Е и направленная под углом 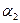 = 30
= 30  к горизонтальной оси).
к горизонтальной оси).
Определить реакции связей в точках А, В, С и К (на рис. 6 в точках А, С, К и Н). При окончательных расчётах принять l = 0,2 м.
Указания. Задача С7 – на равновесие системы двух тел (брусьев), находящихся под действием плоской системы сил. Задачу можно решать двумя путями. Первый: расчленить систему и рассмотреть равновесие каждого из брусьев в отдельности, составив для каждого бруса три уравнения равновесия, и учти при изображении реакций в точке C закон о равенстве действия и противодействия. Второй: сначала рассмотреть равновесие всей системы, составив для неё три уравнения равновесия, а затем расчленить систему рассмотреть равновесие одного из брусьев, составив для него тоже три уравнения равновесия (см. ещё указания к задаче C1).
| Сила | 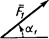 | 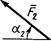 | 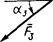 | 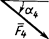 | ||||
| Номер | F 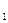 = 10 H = 10 H | F 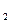 = 20 H = 20 H | F 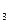 = 30 H = 30 H | F 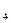 = 40 H = 40 H | ||||
| Точка прилож. | 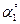 | Точка прилож. | 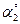 | Точка прилож. | 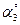 | Точка прилож. | 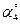 | |
| D | - | - | - | - | - | - | ||
| - | - | E | - | - | - | - | ||
| - | - | - | - | D | - | - | ||
| - | - | - | - | - | - | E | ||
| E | - | - | - | - | - | - | ||
| - | - | D | - | - | - | - | ||
| - | - | - | - | E | - | - | ||
| - | - | - | - | - | - | D | ||
| D | - | - | - | - | - | - | ||
| - | - | E | - | - | - | - |
Таблица C4
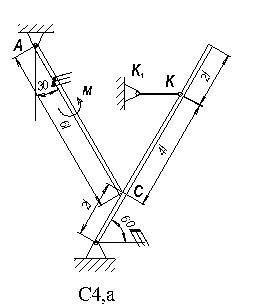
Пример C7. Однородные брусья AC и BD весом соответственно P 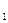 и P
и P 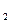 расположены в вертикальной плоскости (рис. C7, а). Брусья свободно опираются друг о друга в точке C, а в точке K брус BD закреплён невесомым стержнем KK
расположены в вертикальной плоскости (рис. C7, а). Брусья свободно опираются друг о друга в точке C, а в точке K брус BD закреплён невесомым стержнем KK 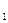 . Все нагрузки, размеры и величины углов показаны на рисунке.
. Все нагрузки, размеры и величины углов показаны на рисунке.
Дано: P 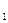 = 15 H, P
= 15 H, P 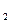 = 25 H, M = 20 Hм , F = 30 H, l = 0,2 м.
= 25 H, M = 20 Hм , F = 30 H, l = 0,2 м.
Определить: реакции связей в точках A, B, C и K.
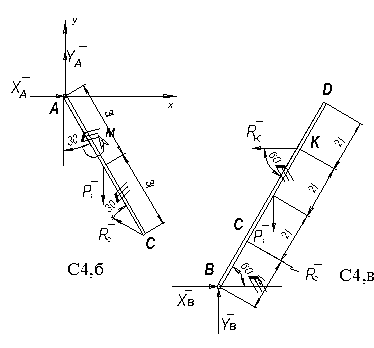
Решение. 1. Расчленяем систему на две части и рассмотрим сначала равновесие бруса AC (рис. C7, б). Проведём координатные оси и изобразим действующие на брус AC силы: силу тяжести 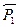 , пару сил с моментом M, реакции связей
, пару сил с моментом M, реакции связей 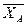 ,
, 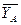 ,
, 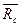 (реакцию неподвижной шарнирной опоры А изображаем двумя её составляющими, реакция
(реакцию неподвижной шарнирной опоры А изображаем двумя её составляющими, реакция 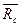 направлена перпендикулярно брусу BD).
направлена перпендикулярно брусу BD).
|
|
|
|
|
|
|
|
|
|
|
|
Для полученной плоской системы сил составим три уравнения равновесия:
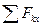 = 0, X
= 0, X 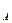 - R
- R 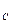 sin 60
sin 60  = 0 (1)
= 0 (1)
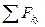 = 0, Y
= 0, Y 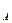 - P
- P 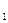 - R
- R 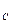 cos 60
cos 60  = 0 (2)
= 0 (2)
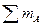 (
( 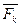 ) = 0, M - P
) = 0, M - P 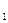
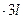 sin 30
sin 30  - R
- R 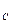
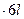 sin 30
sin 30  = 0 (3)
= 0 (3)
2. Теперь рассмотрим равновесие бруса BD (рис. C7, в). На него действуют сила тяжести 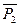 , сила
, сила 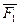 реакции внешних связей
реакции внешних связей 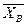 ,
, 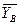 ,
, 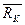 и давление
и давление 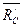 со стороны бруса AC, которое на основании равенства действия и противодействия направлено противоположно силе
со стороны бруса AC, которое на основании равенства действия и противодействия направлено противоположно силе 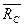 .
.
Для полученной плоской системы сил тоже составим три уравнения равновесия:
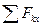 = 0, X
= 0, X 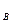 + R
+ R 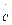 sin 60
sin 60  - R
- R 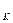 - F cos 15
- F cos 15  = 0, (4)
= 0, (4)
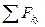 = 0, Y
= 0, Y 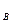 - R
- R 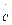 cos 60
cos 60  - P
- P 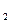 + F sin 15
+ F sin 15  = 0, (5)
= 0, (5)
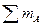 (
( 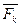 ) = 0, -R
) = 0, -R 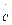
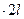 - P
- P 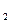
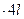 cos 60
cos 60  + R
+ R 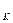
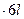 sin 60
sin 60  + F
+ F 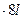 sin 75
sin 75  = 0. (6)
= 0. (6)
Решив систему уравнений (1) – (6) и учтя при этом, что численно R 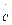 = RС, найдём искомые реакции.
= RС, найдём искомые реакции.
Ответ: XА=22,4 H, YА=2,1 H, XВ=-18,5 H, YВ=30,1 H, RС=25,8 H, RК=-25,1 H. Из полученных результатов видно, что силы 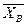 и
и 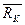 направлены противоположно показанным на рис. C7, в.
направлены противоположно показанным на рис. C7, в.
