Проверка согласованности теоретического и статистического законов распределения с помощью критерия Пирсона

Лаб 2. РЕШЕНИЕ СТАТИСТИЧЕСКИХ ЗАДАЧ СРЕДСТВАМИ MS EXCEL

Произведено 500 измерений боковой ошибки наводки при стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд:

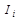	-4;-3	-3;-2	-2;-1	-1;0	0;1	1;2	2;3	3;4

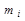Требуется:

1. Вычислить относительные частоты боковой ошибки .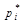

2. Выровнять это распределение с помощью нормального закона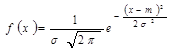

3. Построить сравнительные диаграммы для функций теоретического и экспериментального распределений .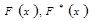

4. Построить сравнительные диаграммы для функций теоретического и экспериментального распределений .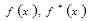

5. Проверить согласованность теоретического и статистического законов распределения по критерию Пирсона.

Указания:

Нормальный закон зависит от двух параметров 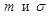. Подберем эти параметры так, чтобы сохранить первые два момента (математическое ожидание и дисперсию статистического распределения).

1. Вычислим сначала относительные частоты боковой ошибки по формуле .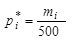

2. Вычислим приближенно статистическое среднее 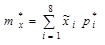ошибки наводки, причем за представителя каждого разряда примем его середину.

3. Для определения дисперсии вычислим сначала второй начальный момент по формуле .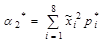

4. Вычислим приближенно дисперсию по формуле 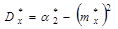и среднеквадратичное отклонение по формуле .

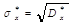Результаты расчетов сведем в таблицу.

Число опытов
Начало разряда	-4	-3	-2	-1
Конец разряда	-3	-2	-1
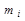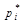	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020
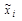	-3,500	-2,500	-1,500	-0,500	0,500	1,500	2,500	3,500
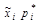	-0,042	-0,125	-0,216	-0,133	0,120	0,264	0,230	0,070
	12,250	6,250	2,250	0,250	0,250	2,250	6,250	12,250
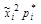	0,147	0,313	0,324	0,067	0,060	0,396	0,575	0,245
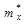	0,168
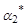	2,126
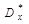	2,098
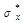	1,448

Выберем параметры 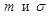нормального закона так, чтобы выполнялись условия 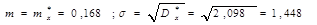. Таким образом .

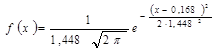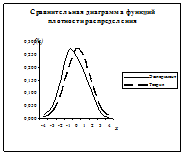
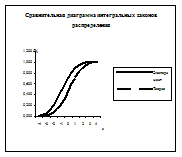
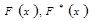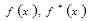Построим теперь сравнительные диаграммы функций распределения и . Для этого вычислим значения законов теоретических и экспериментальных распределений в границах разрядов и построим таблицу:

	-4	-3	-2	-1
f*(x)	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020	0,000
F*(x)	0,012	0,062	0,206	0,472	0,712	0,888	0,980	1,000	1,000
f(x)	0,004	0,025	0,090	0,199	0,274	0,234	0,124	0,041	0,008
F(x)	0,002	0,014	0,067	0,210	0,454	0,717	0,897	0,975	0,996

Для вычисления значений функции 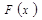следует использовать встроенную функцию Excel НОРМРАСП(x;0,168;1,448;ИСТИНА), а для вычисления значений функции 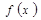– НОРМРАСП(x;0,168;1,448;ЛОЖЬ).

В качестве значений функции 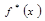следует выбирать частоты 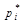, так как все длины разрядов равны единице. Значения функции 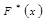вычисляются по формуле .

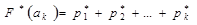Диаграммы с графиками этих функций должна иметь вид:

Проверим теперь правдоподобие гипотезы о виде закона распределения по критерию согласия Пирсона. Заданное статистическое распределение аппроксимировано теоретической кривой.

Между нею и статистическим распределением всегда есть определенные расхождения. Эти расхождения являются следствием либо ограниченного числа наблюдений, либо неудачным выбором вида теоретической кривой.

Для оценки согласованности теоретического и статистического распределений вводят некоторую положительную величину 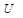, характеризующую степень расхождения теории и эксперимента.

Предполагается, что закон распределения 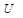известен, а в результате серии опытов выяснилось, что 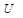приняла некоторое значение u. Очевидно чем меньше величина, u тем вероятнее гипотеза о согласованности и наоборот.

Поэтому количественной оценкой правдоподобия гипотезы служит вероятность события 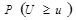, а именно:

Ø если эта вероятность мала – 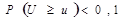, то гипотезу следует отвергнуть как мало правдоподобную (в этом случае вероятность события 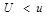велика и расхождение u слишком велико);

Ø если эта вероятность – 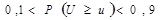, следует признать, что экспериментальные данные не противоречат гипотезе (в этом случае вероятность события 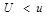мала и расхождение u достаточно мало);

Ø если же эта вероятность значительна – 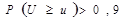, следует признать, что экспериментальные данные очень сильно согласуются с гипотезой и следует проверить, нет ли подтасовки данных.

Пирсон показал, что мера расхождения имеет вид 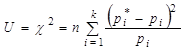или 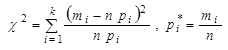. Распределение 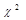зависит от параметра r – числа степеней свободы распределения.

Число 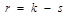, где s число независимых условий (связей), наложенных на частоты 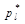. В нашем случае их три

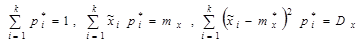
Таким образом схема применения критерия Пирсона 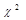имеет вид:

1) Определяется мера расхождения .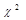

2) Определяется число степеней свободы r = k – s

3) По r и 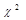определяется вероятность .

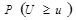Если эта вероятность мала, гипотеза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным.

Проверим согласованность теоретического и статистического законов распределения:

1. Находим вероятности попадания в разряды по формуле

2.

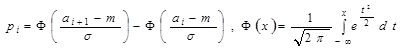
3. Составляем сравнительную таблицу чисел попаданий в разряды 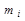и соответствующих значений .

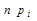4. Вычисляем значение меры расхождения .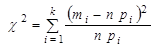

5. Определяем число степеней свободы: .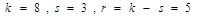

6. Результаты вычислений вносим в таблицу.

Число опытов
Начало разряда	-4	-3	-2	-1
Конец разряда	-3	-2	-1
Число попаданий
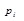	0,012	0,053	0,143	0,244	0,263	0,180	0,078	0,021
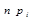	6,171	26,413	71,387	121,939	131,698	89,942	38,828	10,588
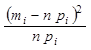	0,005	0,076	0,005	1,003	1,039	0,042	1,325	0,033
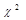	3,527
Вероятность	0,619
Гипотеза правдоподобна

Примечания:

1. Функция 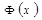– встроена в Excel под именем НОРМСТРАСП.

2. Для определения искомой вероятности следует воспользоваться встроенной функцией Excel ХИ2РАСП( 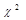; r).

Расчет вероятности по таблице дает 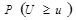= 0,619. Эта вероятность малой не является; поэтому гипотезу о том, что величина 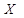распределена по нормальному закону, можно считать правдоподобной.