Деление суждений по модальности

В логике мы до сих пор рассматривали простые суждения, которые называются ассерторическими, а также сложные сужде­ния, составленные из простых. В них утверждается или отрицает­ся наличие определенных связей между предметом и его свойст­вами или констатируется отношение между двумя или большим числом предметов. Например, «Школьники — учащиеся»; «Объ­ем конуса равен 1/3 площади основания, умноженной на высоту»; «Яблоко сладкое и красное»; «Я эту работу не выполню в срок»; «Если будет плохая погода, то мы не поедем на теплоходе» и др. Общая форма таких простых высказываний (суждений): «5 есть (не есть) Р». Из простых суждений образуются сложные. Напри­мер, «Если S есть (не есть) Р, то S₁ есть (не есть) P₁».

В этих ассерторических суждениях не установлен характер связи между субъектом и предикатом. Характер связи между субъектом и предикатом или между отдельными простыми суж­дениями в сложном суждении раскрывается в модальном сужде­нии. Из вышеприведенных суждений можно образовать такие, например, модальные суждения: «Несомненно, что все школь­ники — учащиеся», «Доказано, что в прямоугольном треуголь­нике сумма квадратов катетов равна квадрату гипотенузы», «Хо­рошо, что яблоко сладкое и красное», «Возможно, что я эту работу не выполню в срок», «Вероятно, что если будет плохая погода, то мы не поедем на теплоходе». Мы видим, что модаль­ные суждения не просто утверждают или отрицают некоторые связи, а дают оценку этих связей с какой-то точки зрения.

О предмете А можно просто сказать, что он имеет свойство В (это будет ассерторическое суждение). Но можно сверх того уточнить, является ли эта связь А и В необходимой или, наобо­рот, случайной; хорошо ли, что А есть В или это плохо; доказано, что А есть В или не доказано, а только есть предположение, и т. д. В результате таких уточнений мы получаем модальные суждения различных типов. Приведем другие примеры модаль­ных суждений: «Возможно, на Марсе есть жизнь», «Доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, т. е. а² + b²=с²»; «При красном свете све­тофора проезд транспорта запрещен» и др. В модальном сужде­нии к ассерторическому суждению приписывается тот или иной модальный оператор (модальное понятие): возможно, доказано, необходимо, запрещено, обязательно, плохо и др.Структура простых модальных суждений такая: М (S есть Р) или М (S не есть Р),

где М обозначает модальный оператор (модальное понятие).

Но как было уже сказано, модальными могут быть и сложные суждения. Если а и b — простые суждения, то из сложных ассер­торических суждений: aÙb, aÚb, aÚ×b, a®b, aºb — можно полу­чить соответствующие сложные модальные суждения: M (aÙb); M (aÚb); M (aÚ×b); M (a®b); M (aºb).

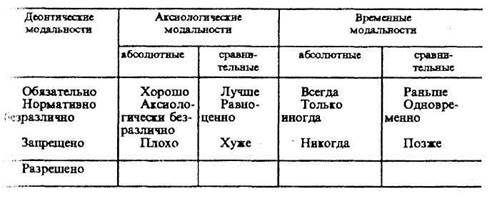
В каждую из групп модальностей входят три основных мо­дальных понятия. Второе из них называется слабой характери­стикой, первое и третье — соответственно сильной положитель­ной и сильной отрицательной характеристиками. Иногда в до­полнение к трем основным модальным понятиям вводится четвертое, которое может употребляться для обозначения объедине­ния сильного положительного и нейтрального.

Логические и онтологические модальности объединяются вобщий вид — алетические модальности¹⁴. Они включают такие модальные операторы или категории модальности: необходи­мость и случайность, возможность и невозможность. Слова «не­обходимо», «возможно», «случайно» в обыденном языке упот­ребляются в самых различных смыслах.

Диалектико-материалистическая философия изучает катего­рии «необходимость», «случайность», «возможность» и другие с их содержательной стороны. Формальная логика изучает суще­ствующие между ними формальные зависимости. Всеобщность модальных категорий состоит в их приложимости к любой об­ласти действительности.

Алетические модальности обозначаются так: «ÿ А» — «необходимо А»; «Ñ А» — «случайно Л»; « ◊ А» — «возможно А»;x~◊A — «невозможно А»(знак «~»обозначает отрицание).

Иногда их обозначают так: «Lp»— «необходимо р», «Мр»— « возможно» .

Алетические модальности (логические и онтологические) ча­сто содержательно истолковывают так: необходимыми считают логические законы, а также законы, выявленные различными науками (естественными, математическими, общественными и техническими), и все следствия из этих законов. Невозможными считают суждения, противоречащие этим законам, отрицания этих законов или их следствий. Случайными считают суждения, не являющиеся законами или их следствиями, но и не противоречащие законам или их следствиям. Возможными считают сложения, не противоречащие законам или их следствиям.Взаимосвязь алетических модальностей

Некоторые алетическне модальности в ряде систем можно определять одну через другую («=» обозначает «равно по опре­делению», «Ù»— конъюнкцию, «Ú» —дизъюнкцию, «~» отрицание, ««»— эквивалентно, «®» — импликацию). Напри­мер,

1А=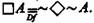

Некоторые важные связи, характеризующие алетические мо­дальности, выражены следующими формулами:

(1) 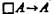(«Earn необходимо, что А, то А»);

(2) 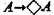(«Если А, то возможно, что А»);

(3) 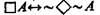(«Необходимо, что А, тогда и только тогда, когда невозможно, что не-А»);

(4) 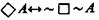(«Возможно, что А, тогда и только тогда, когда не необходимо, что не-А»).