Метод повторного интегрирования правой части

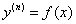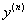Рассмотрим дифференциальное уравнение вида , где – производная «энного» порядка, а правая часть 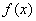зависит только от «икс». В простейшем случае 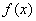может быть константой.

Данное дифференциальное уравнение решается последовательным интегрированием правой части. Причём интегрировать придется ровно 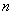раз.

На практике наиболее популярной разновидность является уравнение второго порядка: 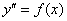. Дважды интегрируем правую часть и получаем общее решение. Уравнение третьего порядка 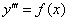необходимо проинтегрировать трижды, и т.д. Но диффуров четвертого и более высоких порядков в практических заданиях что-то даже и не припомню.

Пример 1

Найти общее решение дифференциального уравнения

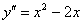
Решение: Данное дифференциальное уравнение имеет вид .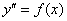

Понижаем степень уравнения до первого порядка:

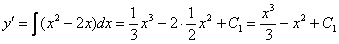
Или короч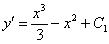е: , где 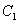– константа

Теперь интегрируем правую часть еще раз, получая общее решение:

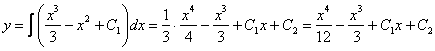
Ответ: общее решение: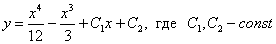

Проверить общее решение такого уравнения обычно очень легко. В данном случае необходимо лишь найти вторую производную:

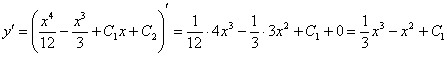
Получено исходное дифференциальное уравнение 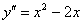, значит, общее решение найдено правильно.

Пример 2

Решить дифференциальное уравнение

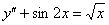
Это пример для самостоятельного решения. Как я уже где-то упоминал, иногда диффур может быть подшифрован. В предложенном примере сначала необходимо привести уравнение к стандартному виду 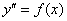. Решение и ответ в конце урока.

Нахождение частного решения (задача Коши) имеет свои особенности, которые мы рассмотрим в следующих двух примерах:

Пример 3

Найти частное решение уравнения, соответствующее заданным начальным условиям

, ,

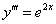
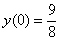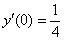Решение:Данное уравнение имеет вид 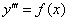. Согласно алгоритму, необходимо последовательно три раза проинтегрировать правую часть.

Сначала понижаем степень уравнения до второго порядка:

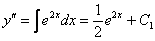
Первый интеграл принёс нам константу 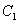. В уравнениях рассматриваемого типа рационально сразу же применять подходящие начальные условия.

Итак, у нас найдено 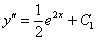, и, очевидно, к полученному уравнению подходит начальное условие .

В соответствии с начальным условием :

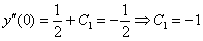
Таким образом: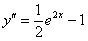

На следующем шаге берём второй интеграл, понижая степень уравнения до первого порядка:

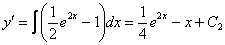
Выползла константа 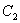, с которой мы немедленно расправляемся. Хах. Комментирую пример, а в голове возникла ассоциация, что я злой дед Мазай с одноствольным ружьём. Ну и действительно, константы отстреливаются, как только покажут уши из-под интеграла.

В соответствии с начальным условием :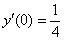

Таким образом: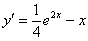

И, наконец, третий интеграл:

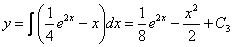
Для третьей константы используем последний патрон :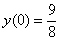

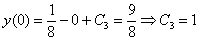
Зайцы плачут, заряды были с солью.

Ответ: частное решение: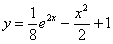

Выполним проверку, благо, она ненапряжная:
Проверяем начальное условие :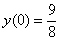
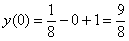– выполнено.

Находим производную:

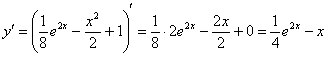
Проверяем начальное условие :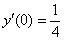
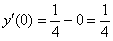– выполнено.

Находим вторую производную:

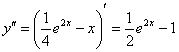
Проверяем начальное условие :
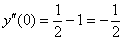– выполнено.

Найдем третью производную:

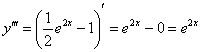
Получено исходное дифференциальное уравнение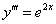

Вывод: задание выполнено верно

Наверное, все обратили внимание на следующую вещь: каков порядок уравнения – столько и констант. Уравнение второго порядка располагает двумя константами 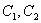, в уравнении третьего порядка – ровно три константы 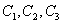, в уравнении четвертого порядка обязательно будет ровно четыре константы 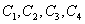и т.д. Причем, эта особенность справедлива вообщедля любого диффура высшего порядка.

Пример 4

Найти частное решение уравнения, соответствующее заданным начальным условиям

, ,

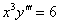
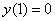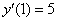Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Время от времени в дифференциальных уравнениях рассматриваемого типа приходится находить более трудные интегралы: использовать метод замены переменной, интегрировать по частям, прибегать к другим ухищрениям. Я намеренно подобрал простые примеры без всяких замысловатостей, чтобы больше внимания уделить именно алгоритму решения.

В дифференциальном уравнении в явном виде отсутствует функция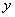

Простейшее уравнение данного типа в общем виде выглядит так:
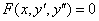– всё есть, а «игрека» нет. Точнее, его нет в явном виде, но он обязательно всплывёт в ходе решения.

Кроме того, вместе с «игреком» в явном виде может отсутствовать первая производная:
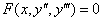– это уже уравнение третьего порядка.

Может дополнительно отсутствовать и вторая производная:
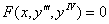– уравнение четвертого порядка.

И так далее. Думаю, все увидели закономерность, и теперь смогут без труда определить такое уравнение в практических примерах. Кроме того, во всех этих уравнениях обязательно присутствует независимая переменная «икс».

На самом деле есть общая формула, строгая формулировка, но я стараюсь избегать лишних параметров и прочих математических наворотов, поскольку уроки носят не теоретический, а практический характер. И даже общие формулы, которые я только что привел, являются не совсем полными с теоретической точки зрения.

Как решать такие уравнения? Они решаются с помощью очень простой замены.

Пример 5

Найти общее решение дифференциального уравнения

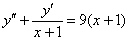
Решение: В данном уравнении второго порядка в явном виде не участвует переменная 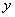. Заменим первую производную 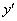новой функцией , которая зависит от «икс»:

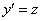
Если 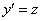, то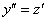

Цель проведённой замены очевидна – понизить степень уравнения:

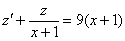
Получено линейное неоднородное уравнение первого порядка, с той лишь разницей, что вместо привычной функции «игрек» у нас функция «зет». Грубо говоря, отличие только в букве.

Линейное неоднородное уравнение первого порядка можно решить двумя способами: методом Бернулли (замены переменной) или методом вариации произвольной постоянной. Я выберу метод вариации произвольной постоянной, поскольку он маловато встречался в моих статьях.

Решим вспомогательное уравнение:

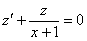
Разделяем переменные и интегрируем:




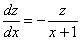
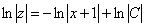
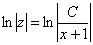
Общее решение вспомогательного уравнения: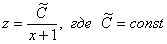

Варьируя постоянную 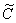, в неоднородном уравнении 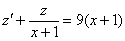проведем замену:

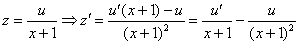
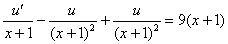
Пара слагаемых в левой части сокращается, значит, мы на верном пути:

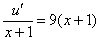
Разделяем переменные и интегрируем:

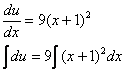
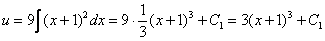
Таким образом:

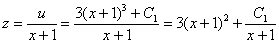
Итак, функция найдена. Тут на радостях можно забыть про одну вещь и машинально записать ответ. Нет-нет, ещё не всё. Вспоминаем, что в начале задания была выполнена замена 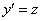, следовательно, нужно провести обратную замену :

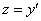Общее решение восстанавливаем интегрированием:

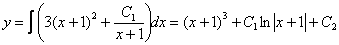
На заключительном этапе нарисовался партизан «игрек», который, как мы помним, в дифференциальное уравнение в явном виде не входил.

Ответ: Общее решение: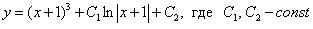

В большинстве случае проверить и такие уравнения не составляет особого труда. Берём полученный ответ, находим первую и вторую производные:

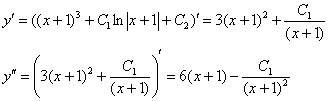
Подставим первую и вторую производную в исходное уравнение :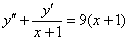

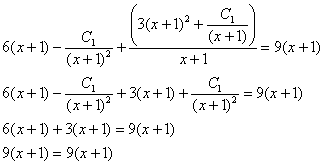
Получено верное равенство, значит, общее решение найдено правильно.

Пример 6

Решить дифференциальное уравнение

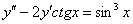
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Теперь вспомним начало заданий. С помощью замены 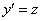мы понижали степень уравнения и получали линейное неоднородное уравнение первого порядка. Всегда ли получается именно линейное уравнение в результате замены? Так происходит часто, но не всегда. После замены 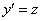может получиться уравнение с разделяющимися переменными, однородное уравнение первого порядка, а также некоторые другие интересности.

Пример 7

Решить дифференциальное уравнение

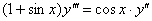
Решение: В данном уравнении третьего порядка в явном виде не участвуют функция 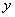и первая производная 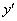. Замена будет очень похожей, за «зет» обозначаем младшего брата:

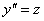
Если 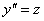, то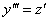

Таким образом, уравнение понижено до первого порядка:

Получено уравнение с разделяющимися переменными, разделяем переменные и интегрируем:

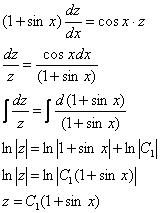
Проведем обратную замену: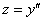

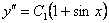
Данное уравнение имеет уже знакомый с первого параграфа вид: .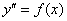

Дважды интегрируем правую часть:

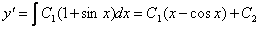
Ответ: общее решение: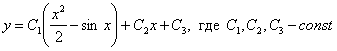

Пример 8

Найти общее решение дифференциального уравнения

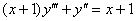
Это пример для самостоятельного решения. После понижения степени получится линейное неоднородное уравнение первого порядка, которое в моём образце решено методом Бернулли. Как говорится, весь арсенал в ходу.

В дифференциальном уравнении
в явном виде отсутствует независимая переменная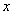

Третий, чуть более сложный тип уравнения, допускающий понижение порядка. Я не буду рисовать общих формул – отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса». Вообще нет. Ни одного. Нигде.

Пример 9

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
, ,

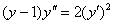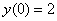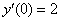
Решение: В данном уравнении в явном виде не участвует переменная 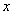. Подстановка здесь более замысловата. Первую производную 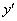заменим некоторой пока еще неизвестной функцией 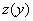, которая зависит от функции «игрек»: 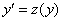. Обратите внимание, что функция 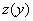– это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).

Находим вторую производную. По правилу дифференцирования сложной функции:

Учитывая, что 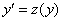, окончательно получаем:

В принципе, можно запомнить данную замену формально и коротко:

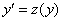
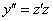
Другой вопрос, что студентам часто не понятно, почему в замене такая странная вторая производная: 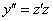, «совершенно же очевидно, что должно быть 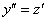». А вот, оно, и не очевидно. Почему 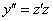, я только что подробно прокомментировал.

Итак, в исходном уравнении 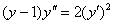проведём нашу замену:

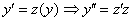
Цель замены – опять же понизить порядок уравнения:

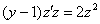
Одно «зет» сразу сокращаем:

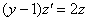
Получено уравнение с разделяющимися переменными. Если 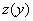– функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так:
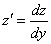. Не допускаем машинальной ошибки – не пишем «привычное» !!!

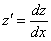Разделяем переменные и интегрируем:

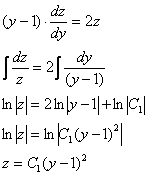
Проведем обратную замену :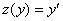

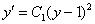
Как и в первом параграфе, константу целесообразно отстрелить незамедлительно, это значительно упростит дальнейшее интегрирование.

Используем оба начальных условия одновременно: ,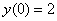

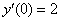
В полученное уравнение 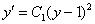подставим 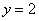и :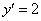

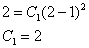
Таким образом:

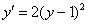
Дальнейшее просто:

Вторую константу тоже отстреливаем. Используя начальное условие 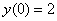, проводим подстановку :

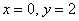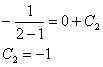
Таким образом: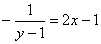

Выразим частное решение в явном виде:

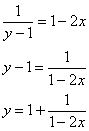
Ответ: частное решение: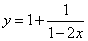

Кстати, ответ легко проверяется.

Для закрепления материала пара заключительных примеров.

Пример 10

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
, ,

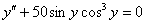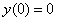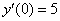
Решение: В данном уравнении в явном виде не участвует переменная 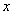. Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:

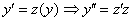
Таким образом, степень уравнения понижена до первого порядка:

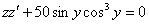
Разделяем переменные и интегрируем, не забывая, что :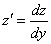

Переобозначим константу 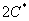через :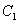
.

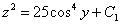Проведём обратную замену :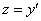

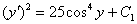
Используем одновременно оба начальных условия 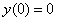, 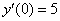и найдём значение константы 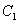. Для этого в полученное уравнение 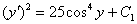подставим 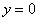и :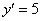

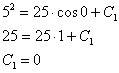
Таким образом:

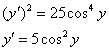
Разделяем переменные и интегрируем:

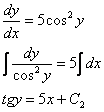
В соответствии с начальным условием :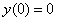

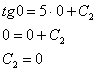
Окончательно: 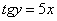или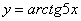

Ответ: частное решение: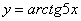

Пример 11

Найти решение задачи Коши.
, ,

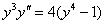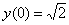Это пример для самостоятельного решения.

Обратите внимание, что все три примера последнего параграфа идут с задачей Коши. Это не случайно. Специфика рассмотренного типа дифференциальных уравнений такова, что если предложить найти общее решение, то в большинстве уравнений нарисуются сложные, вычурные, а то и вообще неберущиеся интегралы. Поэтому практически всегда вам будет предложено найти частное решение.

Существуют еще некоторые типы диффуров, допускающие понижение порядка, но на практике они мне ни разу не встречались, хотя я перерешал очень много дифференциальных уравнений. Поэтому в урок были включены только те примеры, которые вам могут встретиться реально.

А сейчас пора весить ружье на гвоздь и идти пить чай.

Удачного понижения степеней дифференциальных уравнений!

Решения и ответы:

Пример 2: Решение: Преобразуем уравнение: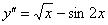
Данное ДУ имеет вид 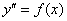. Дважды интегрируем правую часть:


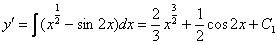
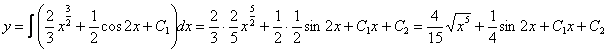
Ответ: общее решение:

Пример 4: Решение: Преобразуем уравнение:
Данное уравнение имеет вид 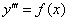. Трижды интегрируем правую часть:

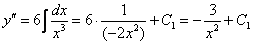
В соответствии с начальным условием:


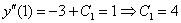
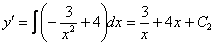
В соответствии с начальным условием:


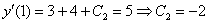
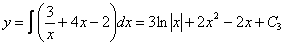
В соответствии с начальным условием:

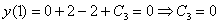
Ответ: частное решение:

Пример 6: Решение: В данное уравнение в явном виде не входит функция 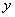, проведем замену: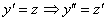

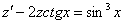
Получено линейное неоднородное уравнение первого порядка. Используем метод вариации произвольной постоянной. Решим вспомогательное уравнение:

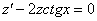
Разделяем переменные и интегрируем:

В неоднородном уравнении проведем замену:


Таким образом:

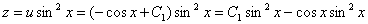
Обратная замена: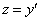

Ответ:Общее решение: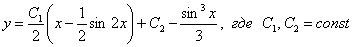

Пример 8: Решение: Проведем замену: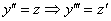

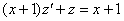
Получено линейное неоднородное уравнение, замена: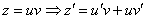

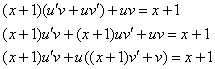
Составим и решим систему: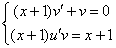
Из первого уравнения найдем :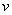

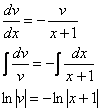
– подставим во второе уравнение:



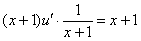
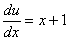
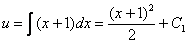
Таким образом: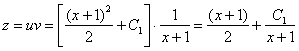
Обратная замена: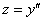

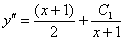
Дважды интегрируем правую часть:


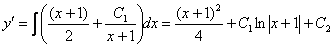
Здесь я немножко схалтурил, интеграл от логарифма берётся по частям, и, строго говоря, последний интеграл нужно расписать подробнее.
Ответ: общее решение:

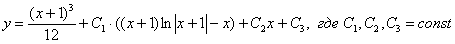
Пример 11: Решение: В данном уравнении в явном виде не участвует переменная 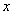, проведем замену: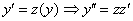

Обратная замена: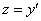

В соответствии с начальными условиями , :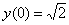


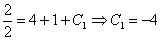
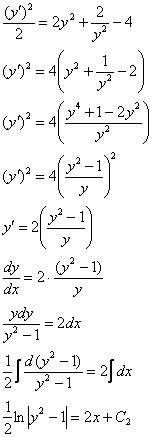
В соответствии с начальным условием :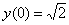


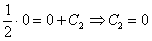
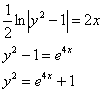
Ответ: частное решение: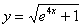

Дифференциальные уравнения второго порядка и высших порядков.
Линейные ДУ второго порядка с постоянными коэффициентами.
Примеры решений.

Переходим к рассмотрению дифференциальных уравнений второго порядка и дифференциальных уравнений высших порядков. Если Вы смутно представляете, что такое дифференциальное уравнение (или вообще не понимаете, что это такое), то рекомендую начать с урока Дифференциальные уравнения первого порядка. Примеры решений. Многие принципы решения и базовые понятия диффуров первого порядка автоматически распространяются и на дифференциальные уравнения высших порядков, поэтому очень важно сначала разобраться с уравнениями первого порядка.

У многих читателей может быть предубеждение, что ДУ 2-го, 3-го и др. порядков – что-то очень трудное и недоступное для освоения. Это не так. Научиться решать диффуры высшего порядка вряд ли сложнее, чем «обычные» ДУ 1-го порядка. А местами – даже проще, поскольку в решениях активно используется материал школьной программы.

Наиболее популярны дифференциальные уравнения второго порядка. В дифференциальное уравнение второго порядка обязательно входит вторая производная 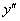и не входят производные более высоких порядков:

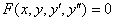
Следует отметить, что некоторые из малышей (и даже все сразу) могут отсутствовать в уравнении, важно, чтобы дома был отец 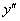. Самое примитивное дифференциальное уравнение второго порядка выглядит так: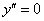

Дифференциальные уравнения третьего порядка в практических заданиях встречаются значительно реже, по моим субъективным наблюдениям в Государственную Думу они бы набрали примерно 3-4% голосов.

В дифференциальное уравнение третьего порядка обязательно входит третья производная 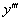и не входят производные более высоких порядков:

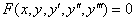
Самое простое дифференциальное уравнение третьего порядка выглядит так: 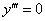– папаша дома, все дети на прогулке.

Аналогичным образом можно определить дифференциальные уравнения 4-го, 5-го и более высоких порядков. В практических задачах такие ДУ проскакивают крайне редко, тем не менее, я постараюсь привести соответствующие примеры.

Дифференциальные уравнения высших порядков, которые предлагаются в практических задачах, можно разделить на две основные группы.

1) Первая группа – так называемые уравнения, допускающие понижение порядка. Налетайте!

2) Вторая группа – линейные уравнения высших порядков с постоянными коэффициентами. Которые мы начнем рассматривать прямо сейчас.

Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
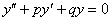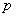, где и 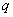– константы (числа), а в правой части – строго ноль.

Неоднородное ДУ второго порядка с постоянными коэффициентамиимеет вид:
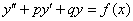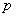, где и 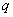– константы, а 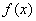– функция, зависящая только от «икс». В простейшем случае функция 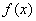может быть числом, отличным от нуля.

Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

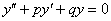
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

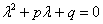
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;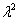
вместо первой производной записываем просто «лямбду»;
вместо функции 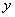ничего не записываем.

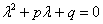– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий. Они доказаны в курсе математического анализа, и на практике мы будем использовать готовые формулы.