Плоские графы. Эйлеровы графы. Гамильтовы графы. Орграфы

Пусть дано непустое множество X, состоящее из элементов, называемых точками (x₁, x₂, …), и на X задано множество отношений T, позволяющих установить соответствие между каждым элементом множества X и некоторым его подмножеством. Каждая пара точек x_i, x_j множества X, между которыми установлено отношение из множества T, называется ребром.

Определение 1. Непустое множество X и множество отношений T называется графом и обозначается G(X,T). Граф называется конечным, если множество X конечно.

С геометрической точки зрения граф G(X,T) представляет собой непустое множество точек (вершин) и множество отрезков (ребер), концы которых принадлежат данному множеству точек. При изображении графов ребра могут быть прямолинейны или криволинейны, длины ребер и расположение вершин произвольно. На следующих рисунках изображен один и тот же граф.

Ребра графа обозначают парой вершин (x₁, x₂).

Определение 2. Вершины, не принадлежащие ни одному ребру графа, называются изолированными.

Пример 1. Рассмотрим граф

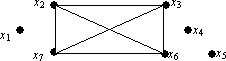
Вершины x₁, x₄, x₅ - изолированные (точка пересечения диагоналей не принадлежит графу). Граф может не иметь ребер. Тогда он состоит из изолированных точек.

Пример 2. Граф

состоит только из изолированных точек.

Определение 3. Две вершины называются смежными, если они соединены ребром, два различных ребра смежные, если они имеют общую вершину.

Определение 4. Ребро и любая из его вершин называются инцидентными.

Определение 5. Ребро графа G(X,T), у которого начальная и конечная вершины совпадают, называется петлей.

Пример 3.Рассмотрим граф

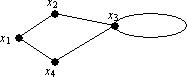
На рисунке ребро (x₃, x₃) является петлей.

Примерами графов могут служить схемы железных дорог, автомобильных дорог, метрополитена, формулы молекул, генеалогические деревья и т.д.

Существуют различные способы задания конечного графа G(X,T). Пусть x₁, x₂, …, x_n - вершины графа, l₁, l₂, …, l_m - ребра графа.

Определение 6. Матрицей смежности называется матрица А_nn, у которой элемент a_ij равен количеству ребер, соединяющих вершины x_i и x_j.

Определение 7. Матрицей инцидентности называется матрица В_nm, у которой элемент b_ij равен 1, если вершина x_i инцидентна ребру l_j, и равен 0 в противном случае.

Пример 4.Для графа

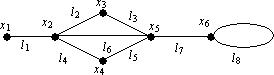
матрицы смежности и инцидентности имеют вид

Графы можно задавать списками пар вершин, соединенных ребрами, или заданием для каждой вершины множества смежных вершин.

Характеристики графа

Определение 1. Граф G(X,T) называется полным, если любые две различные вершины соединены одним, и только одним ребром.

Пример 1. Граф

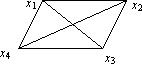
является полным.

В полном графе каждая вершина принадлежит одному и тому же числу ребер, так как она соединена со всеми остальными вершинами. Для задания полного графа достаточно знать число его вершин. Граф, являющийся неполным, можно преобразовать в полный граф с теми же вершинами, добавив недостающие ребра.

Определение 2. Дополнением графа G(X,T) называется граф 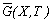с теми же вершинами, что и граф G(X,T), и теми ребрами, которые необходимо добавить к графу G(X,T), чтобы получился полный граф.

Пример 2.

G(X,T) Полный граф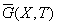

Определение 3. Степенью вершины x_i графа G(X,T) называется число d_i, равное количеству ребер графа, инцидентных этой вершине. Вершина называется четной (нечетной), если ее степень - четное (нечетное) число.

Теорема 1. Если конечный граф G(X,T) (без петель) имеет n вершин и m ребер, то

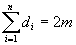. (1)

Доказательство. Рассмотрим граф

Очевидно, что d₁=3, d₂ =2, d₃ =2, d₄ =3. Сложим эти числа:
d₁ + d₂ + d₃ + d₄=10. В этой сумме каждое ребро участвует дважды: 10:5=2.

Рассмотрим произвольный граф G(X,T). Каждая вершина графа x_i инцидентна d_i ребрам. Если сложить эти величины по всем вершинам, то в полученной сумме каждое ребро будет участвовать дважды, т.е. эта сумма будет равна 2m.

Теорема 2.Число нечетных вершин любого графа четно.

Доказательство. Так как левая часть равенства (1) является четным числом, то нечетных вершин должно быть четное число.

Теорема 3. Во всяком графе с n вершинами (n >2) всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.

Доказательство. Предположим противное - все вершины имеют разные степени: 0, 1, 2, …, n - 1. Но если в графе есть вершина степени 0, то не может быть вершины со степенью n - 1. Получено противоречие.

Теорема 4. Если в графе с n вершинами (n >2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени n -1.

Путь и цикл в графе

Определение 1. Путем от x_i до x_j называется такая последовательность ребер графа, ведущая от x_i к x_j , в которой два соседних ребра имеют общую вершину и никакое ребро не встречается дважды. Длиной пути называется число ребер этого пути.

Определение 2. Путь от x_i до x_j называется простым, если он не проходит через одну вершину более одного раза.

Пример 1. Рассмотрим граф

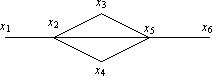
В данном графе есть следующие пути от x₁ до x₆:

1) x₁, x₂, x₅, x₆ - путь длиной 3;

2) x₁, x₂, x₃, x₅, x₆ - путь длиной 4;

3) x₁, x₂, x₄, x₅, x₆ - путь длиной 4;

4) x₁, x₂, x₃, x₅, x₄, x₂, x₅, x₆ - путь длиной 7.

Первые три пути являются простыми.

Определение 3. Циклом называется путь, в котором начальная и конечная вершины совпадают. Длиной цикла называется число ребер в этом цикле.

Определение 4. Цикл называется простым, если он не проходит через одну вершину более одного раза.

Пример 2.Рассмотрим граф

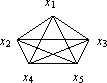
В данном графе есть следующие циклы:

1) x₁, x₅, x₄, x₁ - цикл длиной 3;

2) x₁, x₂, x₃, x₁ - цикл длиной 3;

3) x₁, x₂, x₄, x₅, x₃, x₁ - цикл длиной 5;

4) x₁, x₂, x₄, x₅, x₂, x₃, x₁ - цикл длиной 6;

и т. д.

Первые три цикла являются простыми.

Теорема.Если у графа G(X,T) все простые циклы четной длины, то граф не имеет ни одного цикла нечетной длины.

Доказательство. Предположим противное - в графе есть цикл нечетной длины. В этом цикле найдется вершина, которая повторяется дважды. В этой вершине разобьем цикл на два цикла, из которых один будет иметь четную длину, а второй - нечетную. Опять возьмем цикл нечетной длины и повторим процедуру. За конечное число шагов мы придем к простым циклам, причем один из них будет иметь нечетную длину. Получено противоречие с условием теоремы.