Решение уравнений методом хорд и касательных

Установочные лекции

Семестр (ЗАС)

Методы решения нелинейных скалярных уравнений

def Уравнение 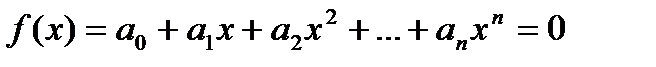, 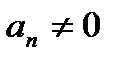- алгебраическое уравнение n-ой степени с n неизвестными. 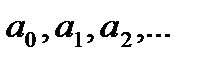- действительные числа.

Если f(x) – трансцендентная функция (показательная, логарифмическая, тригонометрическая и т.д.), то уравнение 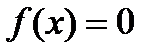называют трансцендентным.

def Корнем уравнения 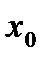(ноль функции) 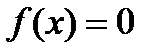называют значение переменной 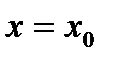, которое обращает уравнение в верное равенство, т.е. .

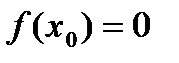В большинстве случаев, корни сложного скалярного уравнения точно найти редко удается. Поэтому большое значение имеют способы приближенного нахождения корней и оценка их точности.

Задача нахождения приближенного значения корня уравнения 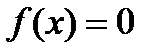состоит из двух шагов:

1)

2)

Способы локализации корней

I. Графический способ локализации корня уравнения .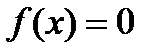

Пример:.

Теорема. Если непрерывная на отрезке 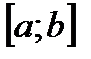функция 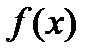на концах его имеет противоположные знаки, т.е. 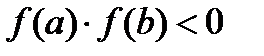, то на интервале 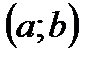она имеет хотя бы один корень. Если же при этом 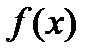строго монотонная, т.е. 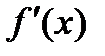не меняет знак на 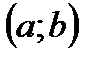, то на 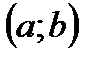существует единственный корень.

II. Метод дихотомии. САМОСТОЯТЕЛЬНО.

III. Метод половинного деления. САМОСТОЯТЕЛЬНО.

Решение уравнений методом хорд и касательных

1. Метод хорд.

Пусть дано уравнение 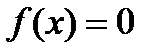, 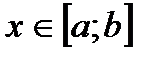и .

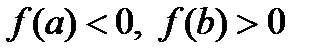Точки графика 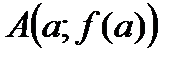и 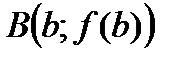соединим хордой.

За приближенное значение искомого корня примем абсциссу 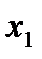точки пересечения хорды АВ с осью Ох.

Это приближенное значение находится по формуле

где .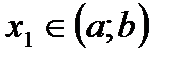

Пусть 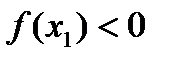, тогда за новый промежуток изоляции корня можно принять 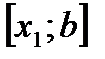. Соединив точк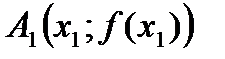и и 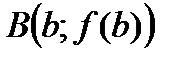, получим в точке пересечения хорды с овью Ох второе приближение 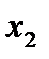, которое вычислим по формуле

и т.д. Последовательность чисел 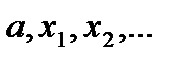стремится к искомому корню уравнения .

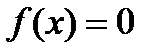Вычисление приближенных значений корней уравнения ведутся до тех пор, пока не будет достигнута заданная степень точности.

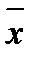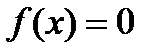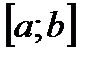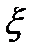Если - точный корень уравнения , изолированный на отрезке , а - приближенное значение корня, найденное методом хорд, то оценка погрешности этого приближенного значения такова:

.

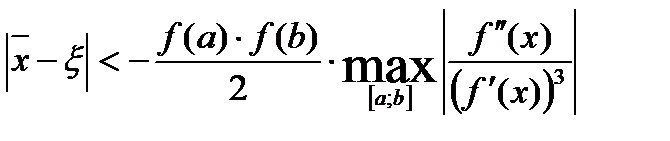2. Метод касательных (метод Ньютона).

Пусть дано уравнение 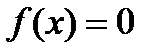, 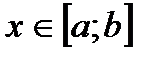и .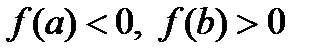

Возьмем на отрезке 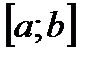такое число 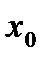, при котором 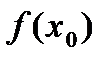имеет тот же знак, что вторая производная 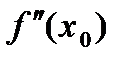, т.е. 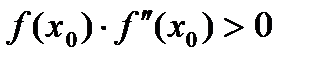(в частности, за 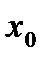может быть принят один из концов интервала, в котором выполняется условие).

Проведем в точке 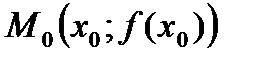касательную к кривой 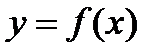. За приближенное значение корня примем абсциссу точки пересечения этой с осью Ох. Это приближенное значение корня находится по формуле

Применив этот прием вторично в точке 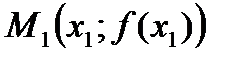, найдем

И т.д. Полученная таким образом последовательность 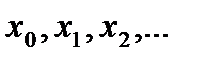имеет своим пределом искомый корень.

Для оценки погрешности приближенного значения корня, найденного методом Ньютона, может быть использовано неравенство

.

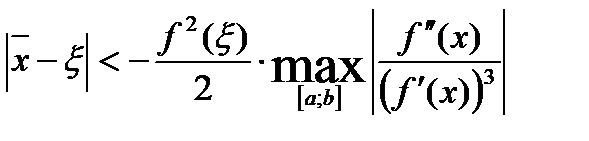3. Метод итераций. САМОСТОЯТЕЛЬНО.

Интерполяция функций

1. Интерполяционный многочлен Лагранжа.

Пусть дана таблица значений

				…
				…

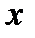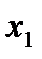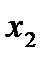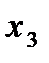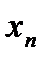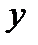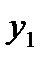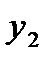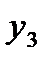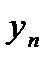Требуется составить многочлен 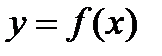степени 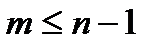, который принимал бы заданные значения 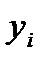при соответствующих значениях 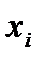, т.е. 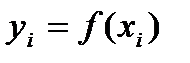. Иными словами, график этого многочлена должен проходить через заданные n точек .

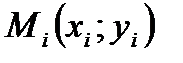Обозначим через

вспомогательный многочлен n-ой степени, в котором 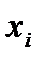- заданные табличные значения аргумента. Тогда имеет место равенство

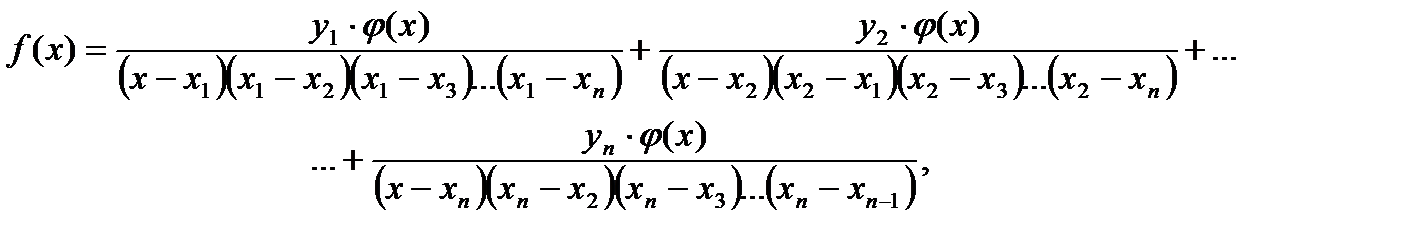
или

.

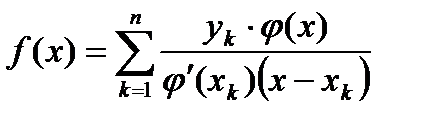Это и есть интерполяционный многочлен Лагранжа.

Пример.

Дана таблица значений

х
у

Составить многочлен Лагранжа. Построить.

Вспомогательный многочлен имеет вид

Найдем 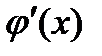при каждых значениях х.

2. Интерполяционная формула Ньютона.

САМОСТОЯТЕЛЬНО.