Нформационные характеристики источников непрерывных сообщений (непрерывных источников сообщений).

ель работы

1.1 Изучение информационных характеристик источников сообщений.

1.2 Приобретение навыков проведения расчетов информационных характеристик дискретных и непрерывных источников сообщений.

лючевые положения

нформационные характеристики источников дискретных сообщений (дискретных источников сообщений).

Источник дискретных сообщений вырабатывает сообщения, состоящие из отдельных знаков, число которых конечно. Под знаком понимают символы, буквы, слова, отдельные фразы и т.п.

Объем алфавита источника М_А – количество различных знаков, используемых источником для построения сообщений.

Количество информации I(a_k), дв. ед. (или бит), в знаке (сообщении) a_k, вероятность появления которого P(a_k), вычисляется

I(a_k) = – log ₂P(a_k). (1)

Энтропия H(A)источника сообщений A – это среднее количество информации в одном знаке. Если знаки сообщений независимы, то энтропия вычисляется как математическое ожидание

H(A) = – 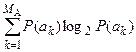. (2)

Энтропия, как и информация, всегда неотрицательная величина и достигает максимального значения

H_max(А) = log₂ M_А,(3)

если знаки независимые и равновероятные.

Избыточность источника сообщений – это свойство источника выдавать информацию бóльшим числом знаков, нежели можно было бы. Наличие избыточности источника сообщений приводит к уменьшению его энтропии.

Коэффициент избыточности источника сообщений характеризует относительное уменьшение энтропии источника по сравнению с ее максимальным значением

К_изб = 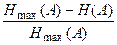.(4)

Производительность источника сообщений, R_и, бит/с, – это среднее количество информации, выдаваемой источником за 1 с

R_и = Н(А)/Т_ср, (5)

где Т_ср – средняя длительность одного знака источника.

нформационные характеристики источников непрерывных сообщений (непрерывных источников сообщений).

Дифференциальная энтропия h(A) источника непрерывных сообщений A вычисляется по формуле

h(A) = – 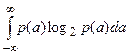, (6)

где p(a) – плотность вероятности сообщения a(t).

Дифференциальная энтропия достигает максимального значения, если распределение вероятностей сообщения гауссовское

h_max(A) = log₂ 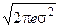, (7)

где σ² – дисперсия сообщения a(t).

Эпсилон-энтропия H_ε(A), дв.ед./отсчет, – это минимальное среднее количество информации в одном отсчете сообщения при заданной допустимой погрешности его приближенного представления ,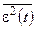

где ;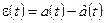

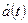– приближенное представление сообщения.

По определению эпсилон-энтропия определяется

H_ε(A) = h(A) – max h(ε), (8)

где h(ε) – дифференциальная энтропия погрешности ε(t).

Максимальное значение h(ε) имеет место при гауссовском распределении ε(t), и расчетная формула для эпсилон-энтропии имеет вид

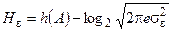, (9)

где 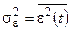– дисперсия погрешности ε(t).

Коэффициент избыточности источника непрерывных сообщений вычисляется по формуле (4) при подстановке соответствующих значений дифференциальных энтропий h(A) и h_max(A).

Эпсилон-производительность R_{и e} источника непрерывных сообщений вычисляется по формуле (5), в которую необходимо подставить значение эпсилон-энтропии H_ε(A), а Т_ср принять равным интервалу дискретизации по Котельникову.

3 Ключевые вопросы

3.1 Дать определение понятия информация.

3.2 Как рассчитать количество информации в сообщении?

3.3 Дать определения информационных характеристик источников сообщений: энтропии, дифференциальной энтропии, эпсилон-энтропии, производительности источника, избыточности источника.

3.4 Какие параметры источника дискретных сообщений необходимо знать, чтобы вычислить его энтропию, избыточность, производительность?

3.5 Какие параметры источника непрерывных сообщений необходимо знать, чтобы вычислить его дифференциальную энтропию, эпсилон-энтропию, производительность, избыточность?

4 Домашнее задание

4.1 Повторить основные положения раздела "Информационные характеристики источников сообщений" по конспекту лекций и учебникам [1, лекции 1, 4; 2, разд. 8.1, 8.2, 8.7; 3, разд. 18.1].

4.2 Вычислить количество информации I, содержащейся в Ваших инициалах (три конкретные буквы) и сравнить его со значением 15 бит (количество информации в трех знаках источника независимых равновероятных знаков с объемом алфавита М_А = 32). Вероятности букв приведены в приложении А. Если I отличается от 15 бит, то пояснить причину отличия.

4.3 Подготовиться к обсуждению по ключевым вопросам.

орядок проведения занятия

Это расчетная лабораторная работа и проводится в таком порядке.

1 Обсуждение ключевых положений и методики расчетов информационных характеристик источников сообщений. Решение типовых примеров, рекомендованных к занятию (пункт 6) или подобранных преподавателем (примерно 50 мин.).

2 Самостоятельная работа студентов (СРС) по индивидуальным билетам (примерно 30 мин.).

Указания. 1. Для вычисления двоичных логарифмов используют соотношения перехода от натуральных и десятичных логарифмов:

log₂ z = ln z/ln 2 »1,443 ln z; log₂ z = lg z/lg 2 » 3,32 lg z.

2. Сообщение непрерывного источника a(t) преобразуется в аналоговый сигнал b(t) без потери информации, поэтому расчеты информационных характеристик источника проводят для сигнала b(t).

иповые примеры

Пример 1. Найти количество информации в слове украинского текста из N = 8 букв. Для расчетов принять, что буквы равновероятные и независимые, объем алфавита М_А = 32.

Ответ: І(слово) = 40 дв. ед.

Пример 2. Вычислить коэффициент избыточности источника двоичных сообщений, если вероятность одного из знаков P(а₁) = 0,1.

Ответ: К_изб = 0,53.

Пример 3. Вычислить производительность источника сообщений, который использует три независимых знака с вероятностями: Р(а₁) = 0,10; Р(а₂) = 0,25; Р(а₃) = ? Длительность первого знака 0,5 мс, второго и третьего по 1 мс.

Ответ: Н(А) = 1300 дв. ед./с.

Пример 4. Рассчитать информационные характеристики источника непрерывных сообщений: эпсилон-энтропию Н_e(В), коэффициент избыточности К_изб, эпсилон-производительность R_{и e}.

Исходные данные: аналоговый сигнал b(t) характеризуется гауссовской плотностью вероятности мгновенных значений р(b) и максимальной частотой спектра F_max = 500 Гц; отношение средней мощности сигнала к средней мощности погрешности представления r = 40 дБ.

Ответ: эпсилон-энтропия Н_e(В) = 6,64 дв.ед./отсчет, коэффициент избыточности К_изб = 0, эпсилон-производительность R_{и e} = 6640 дв.ед./с.

Литература

1.Дирда В.Ю., Іващенко П.В. Теорія електричного зв’язку. Модуль 2. Передавання інформації в телекомунікаційних системах / Навчальний посібник – Одеса: ОНАЗ ім. О.С. Попова, 2010.

2.Стеклов В.К.,Беркман Л.Н. Теорія електричного зв’язку: Підручник для студентів ВУЗів. За ред. В.К. Стеклова – К.: Техніка, 2006.

3. Панфілов І. П., Дирда В. Ю., Капацін А. В. Теорія електричного зв'язку: Підручник для студентів вузів 1-го й 2-го рівнів акредитації. - К.: Техніка, 1998.

Приложение А

Справочные данные для расчетов информационных характеристик

Таблица А.1 – Распределение вероятностей букв в украинских текстах

Буква	Вероятность	Буква	Вероятность	Буква	Вероятность	Буква	Вероятность
Пробел	0,122	Р	0,040	З	0,018	Ж	0,007
О	0,090	С	0,034	Й	0,017	Ц	0,006
А	0,074	Л	0,034	Б	0,016	Ю	0,006
И	0,059	К	0,032	Я	0,015	Ї	0,006
І	0,055	У	0,032	Г	0,013	Є	0,003
Н	0,053	Д	0,026	Ч	0,012	Ф	0,002
В	0,047	П	0,026	Ш	0,010
Т	0,044	М	0,023	Х	0,008
Е	0,041	Ь	0,021	Щ	0,008

Таблица А.2 – Распределение вероятностей букв в русских текстах

Буква	Вероятность	Буква	Вероятность	Буква	Вероятность	Буква	Вероятность
Пробел	0,175	Р	0,040	Я	0,018	Х	0,009
О	0,089	В	0,038	Ы	0,016	Ж	0,007
Е, Ё	0,072	Л	0,035	З	0,016	Ю	0,006
А	0,062	К	0,028	Ь, Ъ	0,014	Ш	0,006
И	0,062	М	0,026	Б	0,014	Ц	0,004
Т	0,053	Д	0,025	Г	0,013	Щ	0,003
Н	0,053	П	0,023	Ч	0,012	Э	0,003
С	0,045	У	0,021	Й	0,010	Ф	0,002

Таблица А.3 – Распределение вероятностей букв в английских текстах

Буква	Вероятность	Буква	Вероятность	Буква	Вероятность	Буква	Вероятность
Пропуск	0,198	R	0,054	U	0,022	V	0,008
E	0,105	S	0,052	M	0,021	K	0,003
T	0,072	H	0,047	P	0,017	X	0,002
O	0,065	D	0,035	Y	0,012	J	0,001
A	0,063	L	0,029	W	0,012	Q	0,001
N	0,059	C	0,023	G	0,011	Z	0,001
I	0,055	F	0,022	B	0.010

Таблица А.4 – Расчетные формулы для дифференциальной энтропии