Проверка адекватности регрессионной модели

Обозначим через дисперсию в i-й точке, – сумму квадратов ошибок в i-й точке.

В качестве примера вычислим и в третьей точке опыта:

Дисперсия наблюдения:

Дисперсия адекватности:

Таблица 7 – Данные для расчёта дисперсии

№
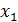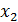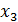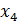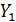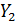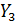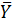	-1	-1	-1	-1				51,33333	9,333333	56,45367	97,32011
	-1	-1	-1					56,66667	9,333333	65,34033	244,3641
	-1	-1		-1						44,32433	463,6676
	-1	-1								53,211	76,80356
	-1		-1	-1				19,66667	1,333333	33,983	617,5389
	-1		-1							42,86967	138,743
	-1			-1				38,66667	9,333333	37,97367	20,10741
	-1									46,86033	1209,299
		-1	-1	-1						51,60167	25,25601
		-1	-1					37,66667	16,33333	42,715	109,1237
		-1		-1						39,47233	923,8473
		-1						29,33333	12,33333	30,58567	29,37168
			-1	-1				23,33333	4,333333	29,131	109,5055
			-1							20,24433	56,0431
				-1				27,66667	2,333333	33,12167	93,93774
								21,33333	0,333333	24,235	25,92567
								39,66667	6,333333	45,64967	120,0555
	-1							61,33333	4,333333	59,38833	20,01574
										36,861	10,22396
		-1						46,33333	129,3333	51,27167	331,8281
								43,33333	9,333333	35,651	195,7214
			-1							39,72033	430,0986
										38,68567	148,0944
				-1				41,33333	9,333333	38,68567	39,69708
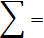									286,6667		5536,58

Вычисляем F-статистику Фишера по формуле:

По таблице П1.3 для и находим .

Так как , то гипотеза об адекватности модели не отвергается. Модель адекватна.

Анализ остатков

Мощным средством для обнаружения некоторых отклонений от исходных предпосылок регрессионного анализа является анализ остатков.

Остатком называется разность между экспериментальными и предсказанными моделью значениями отклика

Анализ остатков позволяет оценить качество разработанных регрессионных моделей и выявить их особенности: выбросы, тренды, сдвиги уровня процесса и т.д. Анализ остатков удобно выполнять графическим способом.

Выбросом называется остаток, который по абсолютной величине значительно превосходит остальные остатки.

Процедура обнаружения выбросов выполняется следующим образом. По оси абсцисс откладывается порядковый номер опыта, а по оси ординат – отношение остатков к среднему квадрату ошибки , который вычисляется по формуле:

Таблица 8 – Данные для обнаружения выбросов

№
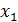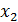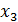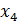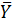	-1	-1	-1	-1	51,33333	56,45367	-5,12033	26,21781	-0,1953
	-1	-1	-1		56,66667	65,34033	-8,67367	75,23249	-0,11529
	-1	-1		-1		44,32433	-12,3243	151,8892	-0,08114
	-1	-1				53,211	4,789	22,93452	0,208812
	-1		-1	-1	19,66667	33,983	-14,3163	204,9574	-0,06985
	-1		-1			42,86967	6,130333	37,58099	0,163123
	-1			-1	38,66667	37,97367	0,693	0,480249	1,443001
	-1					46,86033	-19,8603	394,4328	-0,05035
		-1	-1	-1		51,60167	2,398333	5,752003	0,416956
		-1	-1		37,66667	42,715	-5,04833	25,48567	-0,19809
		-1		-1		39,47233	-17,4723	305,2824	-0,05723
		-1			29,33333	30,58567	-1,25233	1,568339	-0,79851
			-1	-1	23,33333	29,131	-5,79767	33,61294	-0,17248
			-1			20,24433	-4,24433	18,01437	-0,23561
				-1	27,66667	33,12167	-5,455	29,75702	-0,18332
					21,33333	24,235	-2,90167	8,419669	-0,34463
					39,66667	45,64967	-5,983	35,79629	-0,16714
	-1				61,33333	59,38833	1,945	3,783025	0,514139
						36,861	-0,861	0,741321	-1,16144
		-1			46,33333	51,27167	-4,93833	24,38714	-0,2025
					43,33333	35,651	7,682333	59,01825	0,130169
			-1			39,72033	-11,7203	137,3662	-0,08532
						38,68567	-6,68567	44,69814	-0,14957
				-1	41,33333	38,68567	2,647667	7,010139	0,377691
								1654,4

Рисунок 2 – Анализ остатков

Если , то это точка выброса. В нашем случае точками выброса являются 7 и 19 опыты. Точки выброса исключаются из рассмотрения.

Погрешности моделей

Относительную максимальную погрешность вычислим по формуле:

Среднеквадратичное отклонение: