Приведены основы теории и пример решения задачи.

Тема 2. Коэффициент корреляции и линейная регрессия.

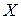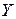1) Пусть нам даны 2 выборки: и объема n. Как оценить силу связи этих переменных?

Решение этой задачи впервые было предложено Пирсоном, который использовал для этого коэффициент корреляции. Коэффициент корреляции Пирсона:

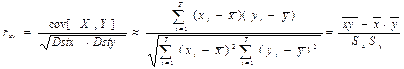
Здесь:

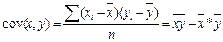- выборочная ковариация.

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < r_xy < 0.3: слабая;
0.3 < r_xy < 0.5: умеренная;
0.5 < r_xy < 0.7: заметная;
0.7 < r_xy < 0.9: высокая;
0.9 < r_xy < 1: весьма высокая;

2. Связь между случайными величинами называется статистической связью. Наличие такой связи заключается в том, что изменение одной из переменных служит причиной для изменения другой. Это можно записать в виде уравнения регрессии y = f(x)+ε. Уравнение регрессии – это формула статистической связи между переменными. Формула статистической связи двух переменных называется парной регрессией и в случае рассмотрения линейной регрессии имеет вид:

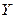=a+b 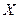+ε – модель парной регрессии.

Чаще всего, Y – зависимая, объясняемая переменная, а Х – независимая, объясняющая переменная.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки линейных параметров регрессий используют метод наименьших квадратов (МНК). Данный метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 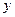от теоретических 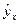минимальна, т.е. .

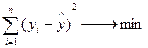Можно воспользоваться готовыми формулами:, ,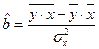

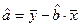
Для оценки качества модели используется коэффициент детерминации R.² . Коэффициент детерминации R² показывает, какая часть (доля) дисперсии результативного признака Y, обусловлена вариацией объясняющей переменной X. Показатель (1-R²) характеризует долю дисперсии 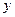, вызванную влиянием остальных, не учтенных в модели факторов. Заметим, что коэффициент детерминации R² имеет смысл рассматривать только при наличии свободного члена в уравнении регрессии. В случае линейной регрессии R² = r² _xy . Коэффициент детерминации (в случае нелинейной регрессии – индекс)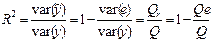

Здесь:

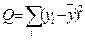Полная сумма квадратов отклонений (общий разброс зависимой переменной)

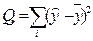Сумма квадратов отклонений регрессии ( разброс, объясняемый регрессией )

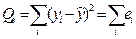Остаточная сумма квадратов отклонений (разброс, не объясняемый регрессией)

где y_i –фактические значения зависимой переменной, 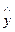- вычисленные по модели регрессии, 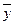- среднее значение зависимой переменной

Если R² незначителен, то следует исследовать другие виды зависимостей.