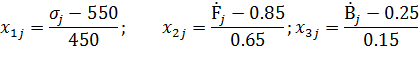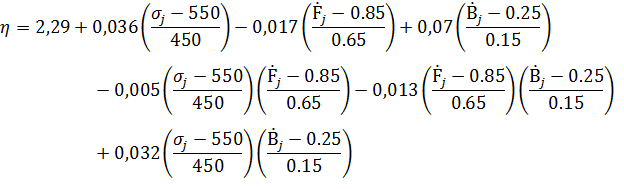Построение квазилинейной регрессионной модели
Лепнев Ю.Г.
Расчётное задание №2 «Планирование эксперимента. Построение линейных и квазилинейных уравнений регрессии»
по дисциплине «Основы научных исследований, организация и планирование эксперимента»
Группа 53304/11
Преподаватель: Востров В.Н.
Санкт-Петербург
Вариант 21
Усилие копания экскаватора R зависит от площади F вырезаемого грунта, ширины ковшаB и прочностью грунта  ,представленных в таблице 1.
,представленных в таблице 1.
Таблица 1 – Зависимость интенсивности напряжений
| Номер |  , МПа , МПа | 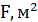 | B, м | 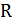 , кН , кН | ||
| 1,5 | 0,4 | 2,41 | 2,25 | |||
| 0,2 | 0,3 | 2,39 | 2,40 | |||
| 1,5 | 0,1 | 2,29 | 2,28 | |||
| 0,2 | 0,1 | 2,29 | 2,25 | |||
| 0,2 | 0,4 | 2,42 | 2,45 | |||
| 1,5 | 0,4 | 2,35 | 2,38 | |||
| 0,2 | 0,2 | 2,32 | 2,30 | |||
| 1,5 | 0,1 | 2,26 | 2,25 | |||
| 1,5 | 0,4 | 2,25 | 2,23 | |||
| 1,5 | 0,2 | 2,20 | 1,15 | |||
| 0,2 | 0,4 | 2,27 | 2,24 | |||
| 0,2 | 0,1 | 2,29 | 2,28 | |||
1. Выбрать из таблицы данные для составления плана эксперимента;
2. Построить квазилинейную регрессионную модель;
3. Выполнить критериальные проверки.
Решение
Составление плана эксперимента
В нашем опыте независимыми переменными являются площадь 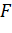 , ширина ковша В и прочности грунта
, ширина ковша В и прочности грунта 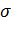 , зависимой переменной является усилие эскаватора R.
, зависимой переменной является усилие эскаватора R.
Для математической обработки данных эксперимента необходимо перейти от реальных физических величин к нормированным, т.е. расположенным в интервале 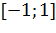 .
.
Интервалы изменения площади вырезаемого грунта, ширины ковша и прочности грунта:
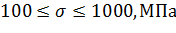
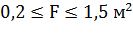
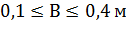 .
.
Вычислим основной уровень для изменения прочности 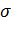 ,ширины ковша В и площади грунтаF:
,ширины ковша В и площади грунтаF:
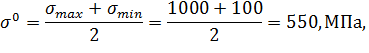
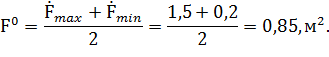
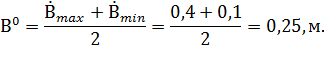
Вычислим интервал варьирования для изменения температуры 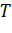 и скорости деформации
и скорости деформации 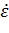 :
:
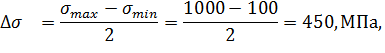
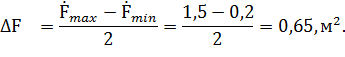
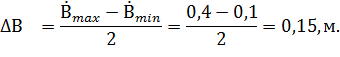
Нормированные значения факторов обозначим через 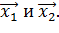
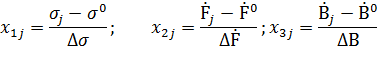
В результате получим план эксперимента:
Таблица 2 – План эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i | 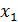 | 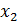 | 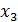 | 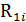 | 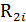 | 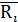 |
| 2,41 | 2,25 | 2,3 | ||||
| -1 | 0,333333 | 2,39 | 2,4 | 2,4 | ||
| -1 | 2,29 | 2,28 | 2,3 | |||
| -1 | -1 | 2,29 | 2,25 | 2,3 | ||
| -1 | 2,42 | 2,45 | 2,4 | |||
| 2,35 | 2,38 | 2,4 | ||||
| -1 | -0,33333 | 2,32 | 2,3 | 2,3 | ||
| -1 | -1 | 2,26 | 2,25 | 2,3 | ||
| -1 | 2,25 | 2,23 | 2,2 | |||
| -1 | -0,33333 | 2,2 | 1,15 | 1,7 | ||
| -1 | -1 | 2,27 | 2,24 | 2,3 | ||
| -1 | -1 | -1 | 2,29 | 2,28 | 2,3 |
Количество опытов в плане полного факторного эксперимента определяется по формуле:
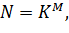 (1.1)
(1.1)
Где K – количество уровней, M – количество факторов.
План эксперимента из таблицы 2 не соответствует соотношению (1.1), так как 12≠63, следовательно необходимо исключить из плана два уровня факторов, чтобы соотношение (1.1.) приняло вид 8=23.
Оставим в плане только максимальные и минимальные уровни факторов, с целью увеличить интервал варьирования и избежать в дальнейшем получения незначимых коэффициентов квазилинейной модели.
Тогда план полного факторного эксперимента примет следующий вид:
Таблица 3 – Планполного факторного эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i | 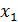 | 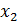 | 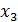 | 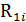 | 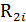 | 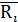 |
| 2,41 | 2,25 | 2,33 | ||||
| -1 | 2,29 | 2,28 | 2,285 | |||
| -1 | -1 | 2,29 | 2,25 | 2,27 | ||
| -1 | 2,42 | 2,45 | 2,435 | |||
| -1 | -1 | 2,26 | 2,25 | 2,24 | ||
| -1 | 2,25 | 2,23 | 2,24 | |||
| -1 | -1 | 2,27 | 2,24 | 2,255 | ||
| -1 | -1 | -1 | 2,29 | 2,28 | 2,285 |
Данный план является полным, т.к. обладает следующими свойствами:
· Алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю. Данное свойство называется симметричностью плана:
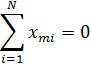
· Сумма почленных произведений любых двух векторов-столбцов равна нулю:
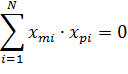
· Сумма квадратов элементов столбца каждого фактора равна количеству опытов N:
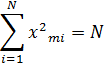
Построение квазилинейной регрессионной модели
Построим квазилинейную статистическую (регрессионную) модель вида:
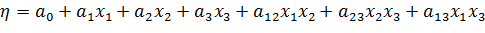
Для нахождения коэффициентов amмодели воспользуемся свойствами вектор-столбцов полного факторного эксперимента. Это позволит вычислить их по формулам:
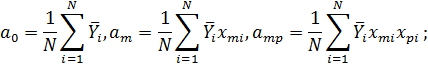
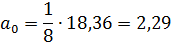
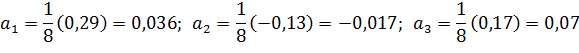
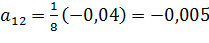 ;
; 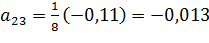 ;
; 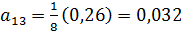
Получили модель:
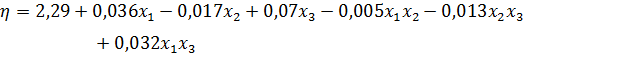
Перейдём от нормированных значений факторов к их натуральным значениям: