Построение регрессионной модели.
Теоретическая часть
Полный факторный эксперимент типа 2к
Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В этом случае, если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных сочетаний уровней факторов.
Формула, которая для этого используется, N = 2к, где N – число опытов, к – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.
Если выбранная модель включает только линейные члены полинома и их произведения, то для оценки всех параметров модели используется план эксперимента с варьированием всех факторов на двух уровнях. Такие планы принято называть планами типа 2n, где 2n=N – число всех возможных опытов, n – количество варьируемых факторов.
Полный факторный эксперимент может быть предложен исследователю как один из способов построения математической модели (идентификации) недетерминированного объекта. Этот способ оказывается наиболее предпочтительным в тех случаях, когда отсутствует априорная информация для обоснования структуры модели с позиций физико-химических представлений процессов, происходящих в объекте, отсутствует количественная оценка степени влияния изучаемых факторов на выходную переменную объекта, его выходной показатель.
Нетрудно написать все сочетания уровней в эксперименте с двумя факторами. Напомним, что в планировании эксперимента используются кодированные значения факторов: +1 и –1 (часто для простоты записи единицы опускают). Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Будем называть такие таблицы матрицами (репликами) планирования эксперимента.
Матрица планирования 22 для двух факторов показана в табл.1
| Номер опыта | Матрица планирования | Выход у | |
| x1 | x2 | ||
| –1 | –1 | y1 | |
| +1 | –1 | y2 | |
| –1 | +1 | y3 | |
| +1 | + 1 | y4 |
Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой.
Таким образом, мы имеем два вектора-столбца независимых переменных и один вектор-столбец параметра оптимизаций. То, что записано в этой таблице в алгебраической форме, можно изобразить геометрически. Найдем в области определения факторов точку, соответствующую основному уровню, и проведем через нее новые оси координат, параллельные осям натуральных значений факторов. Далее, выберем масштабы по новым осям так, чтобы интервал варьирования для каждого фактора равнялся единице. Тогда условия проведения опытов будут соответствовать вершинам квадрата, центром которого является основной уровень, а каждая сторона параллельна одной из осей координат и равна двум интервалам. Номера вершин квадрата соответствуют номерам опытов в матрице планирования. Площадь, ограниченная квадратом, называется областью эксперимента. Иногда удобнее считать областью эксперимента площадь, ограниченную окружностью, описывающей квадрат. В задачах интерполяции область эксперимента есть область предсказываемых значений у.
Запись матрицы планирования, особенно для многих факторов, громоздка. Для ее сокращения удобно ввести условные буквенные обозначения строк.
Это делается следующим образом. Порядковый номер фактора ставится в соответствие строчной букве латинского алфавита: х1 – а, х2 – b, ... и т.д. Если теперь для строки матрицы планирования выписать латинские буквы только для факторов, находящихся на верхних уровнях, то условия опыта будут заданы однозначно. Опыт со всеми факторами на нижних уровнях условимся обозначать (1). Матрица планирования вместе с принятыми буквенными обозначениями приведена в табл. 2.
| Номер опыта | Матрица планирования | Буквенные обозначения строк | Выход у | |
| x1 | x2 | |||
| –1 | –1 | (1) | y1 | |
| +1 | –1 | a | y2 | |
| –1 | +1 | b | y3 | |
| +1 | + 1 | ab | y4 |
Теперь вместо полной записи матрицы планирования можно пользоваться только буквенными обозначениями, Ниже приведена буквенная запись еще одного плана: с, b, a, abc, (1), bc, aс, ab. Матрица планирования приведена в табл. 3.
| Номер опыта | х1 | х2 | х3 | Буквенные обозначения строк | у |
| –1 | –1 | +1 | c | у1 | |
| –1 | +1 | –1 | b | у2 | |
| +1 | –1 | –1 | a | у3 | |
| +1 | +1 | +1 | abc | у4 | |
| –1 | –1 | –1 | (1) | у5 | |
| –1 | +1 | +1 | bc | у6 | |
| +1 | –1 | +1 | ac | у7 | |
| +1 | +1 | –1 | ab | у8 |
Таким образом, вы построили полный факторный эксперимент 23. Он имеет восемь опытов и включает все возможные комбинации уровней трех факторов.
Если для двух факторов все возможные комбинации уровней легко найти прямым перебором (или просто запомнить), то с ростом числа факторов возникает необходимость в некотором приеме построения матриц. Из многих возможных обычно используется три приема, основанных на переходе от матриц меньшей размерности к матрицам большей размерности. Рассмотрим первый. При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда естественно появляется прием: записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня. Вот как это выглядит при переходе от эксперимента. Этот прием распространяется на построение матриц любой размерности.
Рассмотрим второй прием. Для этого введем правило перемножения столбцов матрицы. При построчном перемножении двух столбцов матрицы произведение единиц с одноименными знаками дает +1, а с разноименными –1. Воспользовавшись этим правилом, получим для случая, который мы рассматриваем, вектор-столбец произведения х1х2 в исходном плане. Далее повторим еще раз исходный план, а у столбца произведений знаки поменяем на обратные Этот прием тоже можно перенести на построение матриц любой размерности, однако он сложнее, чем первый.
Третий прием основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т.д. по степеням двойки.
По аналогии с полным факторным экспериментом 22 можно дать геометрическую интерпретацию полного факторного эксперимента 23. Геометрической интерпретацией полного факторного эксперимента 23 служит куб, координаты вершин которого задают условия опытов.
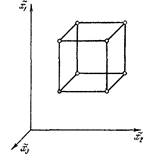 Если поместить центр куба в точку основного уровня факторов, а масштабы по осям выбрать так, чтобы интервал варьирования равнялся единице, то получится куб, изображенный на рис. Куб задает область эксперимента, а центр куба является ее центром.
Если поместить центр куба в точку основного уровня факторов, а масштабы по осям выбрать так, чтобы интервал варьирования равнялся единице, то получится куб, изображенный на рис. Куб задает область эксперимента, а центр куба является ее центром.
Фигура, задающая область эксперимента в многомерном пространстве, является некоторым аналогом куба. Будем называть эту фигуру гиперкубом.
Свойства полного факторного эксперимента типа 2k
Мы научились строить матрицы планирования полных факторных экспериментов с факторами на двух уровнях. Теперь выясним, какими общими свойствами эти матрицы обладают независимо от числа факторов. Говоря о свойствах матриц, мы имеем в виду те из них, которые определяют качество модели. Ведь эксперимент и планируется для того, чтобы получить модель, обладающую некоторыми оптимальными свойствами. Это значит, что оценки коэффициентов модели должны быть наилучшими и что точность предсказания параметра оптимизации не должна зависеть от направления в факторном пространстве, ибо заранее неясно, куда предстоит двигаться в поисках оптимума.
Два свойства следуют непосредственно из построения матрицы. Первое из них – симметричность относительно центра эксперимента – формулируется следующим, образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, или 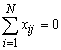 , где j – номер фактора, i – номер опыта, N – число опытов.
, где j – номер фактора, i – номер опыта, N – число опытов.
Второе свойство – так называемое условие нормировки – формулируется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов, или 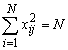 . Это следствие того, что значения факторов в матрице задаются +1 и –1.
. Это следствие того, что значения факторов в матрице задаются +1 и –1.
Мы рассмотрели свойства отдельных столбцов матрицы планирования. Теперь остановимся на свойстве совокупности столбцов.
Сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или 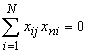 , j¹n.
, j¹n.
Это важное свойство называется ортогональностью матрицы планирования.
Последнее, четвертое свойство называется ротатабельностью, т.е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.
Даны две матрицы планирования:
x1 x2 x1 x2
– – – +
+ – + –
– + – +
+ + + –
Давайте проверим, как выполняются все три свойства для каждой из матриц. Первое свойство выполняется для всех столбцов обеих матриц. Действительно, для первого столбца матрицы а) имеем
(– 1) + (+1) + (- 1) + (+ 1) = 0.
Аналогичный результат получается для всех других столбцов.
Второе свойство– также выполняется для обеих матриц.
С третьим свойством, однако, дело обстоит иначе. Если для матрицы а) формула ортогональности выполняется, то в случае б) это не так. Действительно (–1) (+ 1) + (+ 1) (– 1) + (– 1) (+ 1) + (+1)(–1) = –4≠0.
Полный факторный эксперимент и математическая модель
Давайте еще раз вернемся к матрице 23. Для движения к точке оптимума нам нужна линейная модель у = b0 + b1x1+ b2х2. Наша цель – найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели, мы не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель η = β0 + β1x1+ β2х2 адекватна. Греческие буквы использованы для обозначения «истинных» генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет только получить выборочные оценки для коэффициентов уравнения у = b0 + b1x1 + … + bkхk. Их точность и надежность зависят от свойств выборки и нуждаются в статистической проверке.
После проведения опытов во всех точках факторного пространства необходимо найти коэффициенты уравнения регрессии. Для этого воспользуемся методом наименьших квадратов.
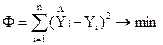 ;
;
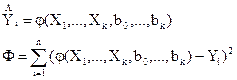 , поскольку
, поскольку 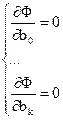 ,
,
то после дифференцирования получим
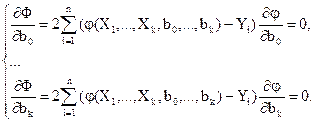
Для линейной регрессии при k=2:
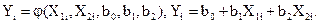 ;
;
продифференцировав по коэффициентам, получим:
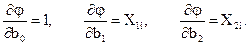
Запишем уравнения в полной форме:
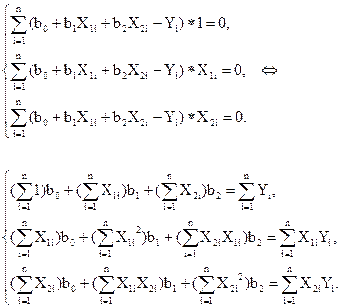
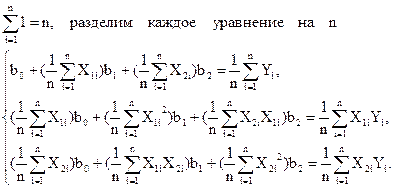
Отсюда, принимая в расчет свойства матрицы планирования, получим следующие формулы для вычисления коэффициентов
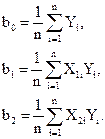
или в общем виде 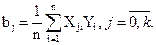
Вы видите, что благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру.
Для подсчета коэффициента b1 используется вектор-столбец х1 а для b2 – столбец х2. Остается неясным, как найти b0. Если наше уравнение у = b0 + b1x1+ b2х2 справедливо, то оно верно и для средних арифметических значений переменных: 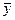 = b0 + b1
= b0 + b1 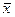 1+ b2
1+ b2 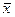 2. Но в силу свойства симметрии
2. Но в силу свойства симметрии 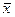 1 =
1 = 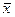 2 = 0. Следовательно,
2 = 0. Следовательно, 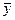 = b0. Мы показали, что b0 есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все у и разделить на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной x0, которая принимает во всех опытах значение +1. Это было уже учтено в записи формулы, где j принимало значения от 0 до к.
= b0. Мы показали, что b0 есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все у и разделить на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной x0, которая принимает во всех опытах значение +1. Это было уже учтено в записи формулы, где j принимало значения от 0 до к.
Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели
у = b0 + b1x1+ b2х2
Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением значения фактора параметр оптимизации увеличивается, а если минус, то уменьшается. Величина коэффициента соответствует вкладу данного фактора в величину параметра оптимизации при переходе фактора с нулевого уровня на верхний или нижний.
Иногда удобно оценивать вклад фактора при переходе от нижнего к верхнему уровню. Вклад, определенный таким образом, называется эффектом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту. Для качественных факторов, варьируемых на двух уровнях, основной уровень не имеет физического смысла. Поэтому понятие «эффект фактора» является здесь естественным.
Планируя эксперимент, на первом этапе мы стремимся получить линейную модель. Однако у нас нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели. А если модель не линейна, как количественно оценить нелинейность, пользуясь полным факторным экспериментом?
Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 22 матрица планирования с учетом эффекта взаимодействия представлена в табл.4 Очень важно, что при добавлении столбцов эффектов взаимодействий все рассмотренные свойства матриц планирования сохраняются.
Матрица планирования эксперимента 22 с учетом взаимодействия факторов
| Номер опыта | х0 | х1 | х2 | х1х2 | у |
| +1 | –1 | –1 | +1 | у1 | |
| +1 | +1 | –1 | –1 | у2 | |
| +1 | –1 | +1 | –1 | у3 | |
| +1 | +1 | +1 | +1 | у4 |
Теперь модель выглядит следующим образом:
у= b0 х0 + b1 x1 + b2 x2 + b12х1х2.
Коэффициент b12 вычисляется обычным путем.
Столбцы x1 и х2 задают планирование – по ним непосредственно определяются условия опытов, а столбцы х0 и х1х2 служат только для расчета.
Обращаем ваше внимание на то, что при оптимизации мы стремимся сделать эффекты взаимодействия возможно меньшими.
Цель работы:приобретение навыков полнофакторного планирования, построения и оценки адекватности регрессионных моделей
Выполнение работы
Регрессионный анализ
По электронному шаблону на предоставленных данных исследуется простейший случай линейной регрессии.
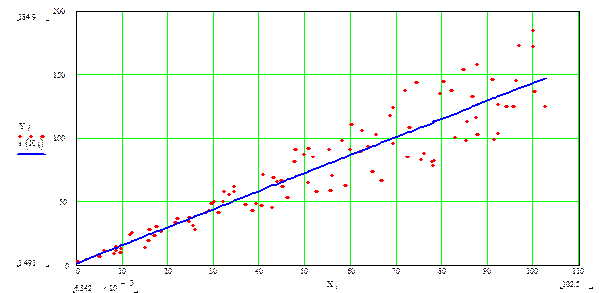
Рисунок 1 – Линейная регрессия
Рассчитываются доверительные интервалы для коэффициентов регрессии. Находится доверительная область для всей линии регрессии.
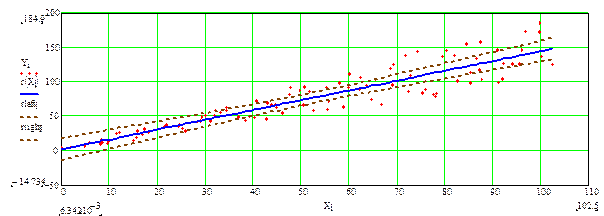
Рисунок 1 – Линейная регрессия и доверительная область
Задание к части 1.
1) Используя функцию для генерации случайных чисел создать двумерный массив данных, распределенных по линейному закону с добавлением шума. Провести обработку, аналогичную приведенному примеру.
2) Дополните матрицу наблюдения D тремя столбцами, два из них должны иметь математическое ожидание как у D(1), а дисперсию меньше (больше). Третий заполняется построчным средним. Проведите всё исследование для этого столбца и сформулируйте заключение о влиянии дополнительных экспериментов для соответствующих интервальных оценок.
Лабораторная работа 2
Полнофакторное планирование эксперимента
Дан план эксперимента и функции отклика системы
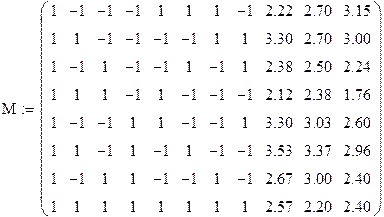
Находятся значения и значимость коэффициентов регрессионной модели:
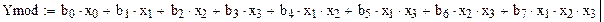
Для откорректированной модели:
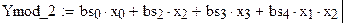
проводится проверка адекватности модели по критерию Фишера.
Пример выполнения лабораторной работы 1
Цель работы: «Приобретение навыков полнофакторного планирования, построения и оценки адекватности регрессионных моделей».
Порядок выполнения работы:
Часть 1
1. Регрессионный анализ.
2. Точечная оценка.
3. Уравнение линейной регрессии.
4. Проверка значимости оценок.
5. Нахождение доверительных интервалов
Вывод.
Часть 2
6. Полный факторный эксперимент.
7. Функция отклика.
8. Матрица планирования.
9. Обработка результатов законченного эксперимента.
10. Проверка значимости коэффициентов регрессии.
11. Дисперсия адекватности регрессии.
12. Проверка адекватности модели.
Вывод
Ход работы.
Вывод.
Регрессионный анализ – статистический метод исследования, позволяющий определять степень детерминированности вариации зависимых переменных от независимых. Уравнение регрессии отображает зависимость между результативным и факторным признаками, позволяет предсказывать возможные значения исследуемой функции.
Лабораторная работа 2.
План эксперимента удобно задавать таблицей, называемой матрицей планирования эксперимента, включающей в себя последовательность проведения опытов, значения факторов и эффектов их взаимодействий, а также значения исследуемой функции, называемой функцией отклика.
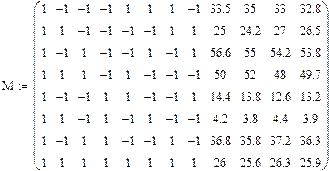
В матрице представлены следующие вектор-столбцы: первый - фиктивной переменной, во всех опытах его значение равно +1, второй-четвертый – являются линейными коэффициентами, пятый-восьмой – эффекты взаимодействия линейных коэффициентов, девятый-двенадцатый – значения функции отклика, полученные в результате проведения экспериментов.
Обработка результатов эксперимента.
План статистической обработки результатов законченного эксперимента:
1. Нахождение дисперсии воспроизводимости.
2. Проверка значимости отдельных коэффициентов регрессии.
3. Определение оценки дисперсии адекватности.
4. Проверка адекватности полученной математической модели.
Находим среднеквадратическое отклонение:
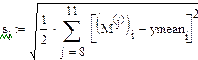
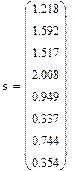
Пользоваться построчными средними для определения коэффициентов полинома можно, только если построчные дисперсии являются однородными. При равномерном дублировании опытов однородность ряда построчных дисперсий определяется по критерию Кохрена. Из таблицы (Рис №5) определим значение G-критерия для уровня значимости α=0.05 чисел степеней свободы f1 – количество опытов для каждого плана - 1 и f2 – число экспериментов.
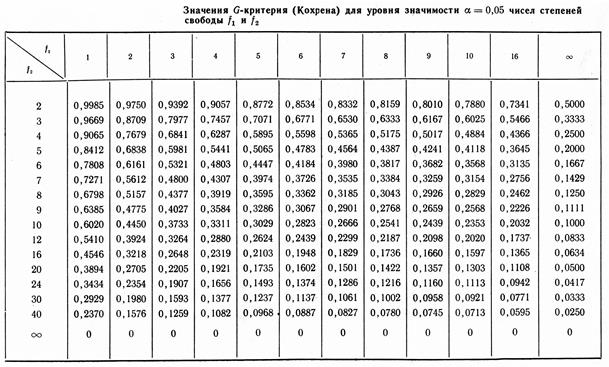
Рисунок 7 – Таблица Кохрена
f1 = 4-1=3, f2 =8:
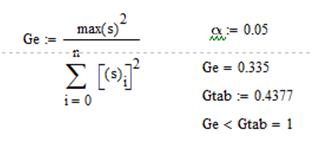
Так как Ge<Gtab, то ряд дисперсий считается однородным и значит, использование построчных средних допустимо.
Воспользуемся строчной средней для нахождения коэффициентов модели:
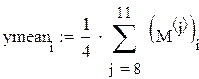
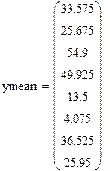
Находим коэффициенты модели:
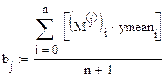
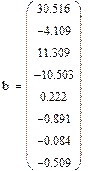
Получаем полнофакторную модель:
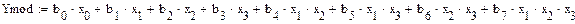
Вывод.
Полнофакторный эксперимент – эксперимент, в котором реализуются все возможные сочетания уровней рассматриваемых факторов. Исследователь имеет возможность управлять состояниями факторов и получать значение функции отклика, занося результаты экспериментов в матрицу планирования. Далее по полученной матрице находятся коэффициенты модели. Затем проверяется адекватность полученной модели. Если модель адекватна, значит, она правильно воспроизводит результаты реального эксперимента и готова к использованию.
Выполнение работы
1. В соответствии с последней цифрой в зачетной книжки выберите вариант с функцией плотности распределения из табл. 1, сравните её описание с формой, представленной в примере.
2. Постройте поверхности отклика для математического ожидания или дисперсии по формуле и по регрессии, полученной в виртуальном эксперименте.
3. Сделайте заключение относительно сходства (различия) этих поверхностей.
Таблица 7 – Варианты к работе.
| № п/п | Наименование | Обозначение, параметры масштаба и формы | Плоность распределения вероятностей и моменты m и D |
| Равномерное распределение | 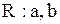 | 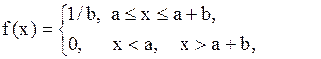 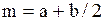 , , 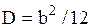 . Алгоритм генерации . Алгоритм генерации 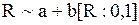 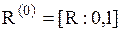 – стандартный датчик равновероятной случайной величины в диапазоне – стандартный датчик равновероятной случайной величины в диапазоне 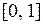 . . | |
| Нормальное распределение | 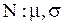 | 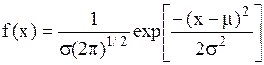 , , 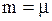 , , 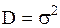 . Алгоритм генерации . Алгоритм генерации 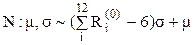 . . | |
| Экспоненциальное распределение | 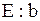 | 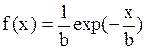 , , 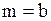 , , 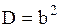 . Алгоритм генерации . Алгоритм генерации 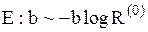 | |
| Логнормальное распределение | 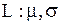 | 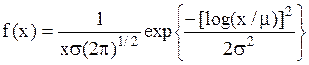 , , 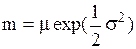 , , 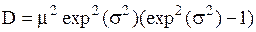 . Алгоритм генерации . Алгоритм генерации 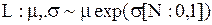 | |
| Гамма-распределение | 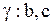 | 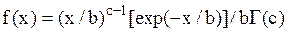 , , 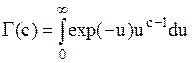 – гамма-функция, – гамма-функция, 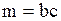 , , 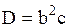 . Алгоритм генерации . Алгоритм генерации 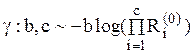 | |
| Бета-распределение | 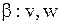 | 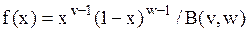 , , 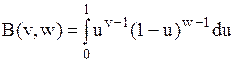 – бета-функция, – бета-функция, 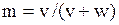 , ,  . Алгоритм генерации . Алгоритм генерации 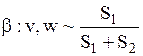 , , 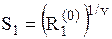 , , 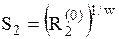 , , 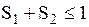 | |
| Распределение экстремального значения | 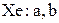 | 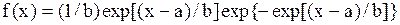 , , 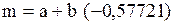 , , 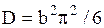 . Алгоритм генерации . Алгоритм генерации 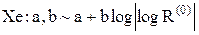 | |
| Логистическое распределение | 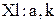 | 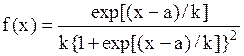 , , 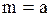 , , 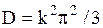 . Алгоритм генерации . Алгоритм генерации 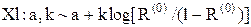 | |
| Распределение Вейбулла | 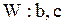 | 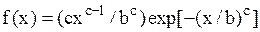 , , 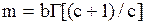 , , 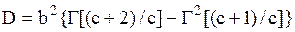 . Алгоритм генерации . Алгоритм генерации 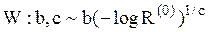 | |
| Распределение Эрланга | 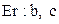 (е – целое) (е – целое) | 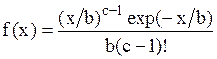 , , 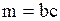 , , 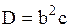 . Алгоритм генерации . Алгоритм генерации 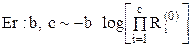 |
Пример выполнения лабораторной работы № 2
Цель работы: «Приобрести навыкполнофакторного и дробнофакторного планирования экспериментов и построения адекватных регрессионных моделей в среде MathCad».
Порядок выполнения работы:
1. Выбрать функцию плотности распределения из таблицы, в соответствии с вариантом.
2. Построить поверхность отклика для математического ожидания или дисперсии по формуле и по регрессии, полученной в виртуальном эксперименте.
3. Сделать заключение относительно сходства (различия) этих поверхностей.
Ход работы
В соответствии с вариантом была выбрана функция распределения, представленная в таблице 8.
Таблица 8 – Функция плотности распределения
| № п/п | Наименование | Обозначение, параметры масштаба и формы | Плотность распределения вероятностей и моменты m и D | Алгоритм генерации |
| Равномерное распределение | 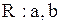 | 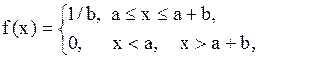 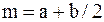 , , 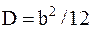 . . | 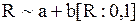 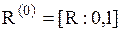 – стандартный датчик равновероятной случайной величины в диапазоне – стандартный датчик равновероятной случайной величины в диапазоне 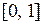 |
.
Задача заключается в следующем: по заданному алгоритму генерации и закономерностям расчета математического ожидания и дисперсии, спланировав эксперимент, построить некую общую модель. Далее спроектировать программную реализацию теоретических математических моделей и сравнить ее результаты с «эталонной» моделью.
Стратегическое планирование эксперимента.
На первом этапе необходимо сформировать левую часть матрицы планирования эксперимента. Предположим, что будет достаточно построения модели полнофакторного эксперимента 22, т.е. матрицы, состоящей из 4-х опытов.
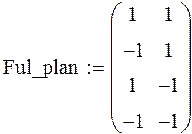
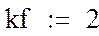
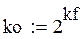
где kf – количество факторов, ko – количество опытов.
Реальные значения каждого фактора варьируются от минимального к максимальному значению. Количество уровней факторов может принимать несколько значений, в нашем случае используются 2 кодированных значения: максимальное «+1» и минимальное «-1». Так же матрица планирования должна содержать столбец фиктивной переменной и столбец взаимодействия факторов.
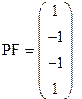
Добавим фиктивный столбец в матрицу планирования:
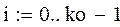
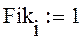
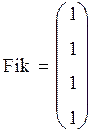
Столбец взаимодействия, состоящий из построчных произведений значений рассматриваемых факторов, будет иметь вид:
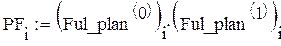
Зададим произвольно минимальные и максимальные значения факторов:
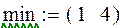
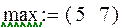
Произведем подстановку реальных значений факторов. Вместо минимального (максимального) значения подставляем минимальное (максимальное) значение соответствующего фактора и получаем следующую матрицу:
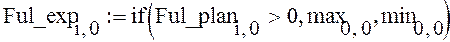
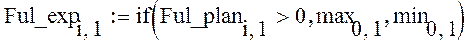
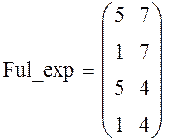
Экспериментальная матрица готова. С помощью функции augment(X1, X2,..,Xn) соединим ее части в матрицу вида:
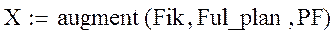
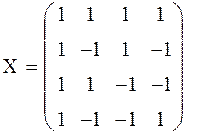
Тактическое планирование виртуального эксперимента.
Задача этого этапа заключается в определении количества опытов таким образом, чтобы при заданном уровне значимости, достигнуть уровень относительной ошибки оценки показателя эффективности.
Уровень относительной ошибки – показатель, зависящий от количества ошибок исследователя или системы. При проведении экспериментов зачастую используется доверительная вероятность – 95%, откуда и определяется уровень значимости по формуле:
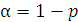 , где доверительная вероятность.
, где доверительная вероятность.
α=0,05.
Выберем уровень относительной ошибки равный 0,15 и рассчитаем квантиль нормального распределения и количество опытов:
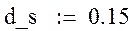
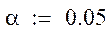
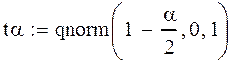
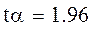
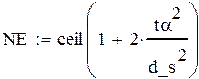
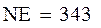
В каждой строке плана будет проведено 343 эксперимента.
Вывод
В ходе планирования эксперимента были построены математические модели: экспериментальная и теоретическая (по математическому ожиданию и по дисперсии). По моделям были получены функции отклика, которые мы сравнили с экспериментальной функцией отклика (графически и численно). По рассчитанным коэффициентам корреляции видно, что функция отклика, построенная по математическому ожиданию, является точнее, т.е. воспроизводит результаты эксперимента лучше, ближе к реальному эксперименту. Следовательно, ее можно взять за основу проведения виртуального эксперимента.
Лабораторная работа 3. Рассмотрение методики диагностики оборудования на примере электроприводной арматур
Теоретическая часть.
Диагностические параметры сигналов активной мощности и токовых сигналов ЭПА
Анализ неисправностей электрических машин, опыт эксплуатации ЭПА показывает, что для определения вида технического состояния (оценки работоспособности) электроприводной арматуры, находящейся в составе технологических систем энергоблоков ТЭС и АЭС, достаточно информативным является токовый сигнал (сигнал активной мощности) электродвигателя, рассчитанный для одной и/или трех фаз.
В результате анализа кинематических схем приводов и данных измерений сигналов тока и активной мощности была принята за эталон циклограмма сигналов активной мощности «открытие-закрытие» идеальной модели ЭПА, где координаты точек и геометрические параметры отрезков циклограмм используются для расчета диагностических параметров технического состояния арматуры.
Циклограммы содержат необходимые признаки, характеризующие динамику перемещения и кинематические особенности передаточных звеньев исполнительных механизмов арматуры, электропривода и электродвигателя.
На рисунках 10 и 11 приведена типичная форма токового сигнала (сигнала активной мощности), регистрируемого при выполнении операции «Открытие» и «Закрытие» при отсутствии расхода рабочей среды. Под формой токового сигнала понимается огибающая переменной составляющей исходного токового сигнала. Приведенная форма сигналов характерна для задвижек. Для регулирующих клапанов и вентилей форма сигнала может отличаться от формы, приведенной на рисунках 3 и 4 (например, отсутствием тока срыва и уплотнения).
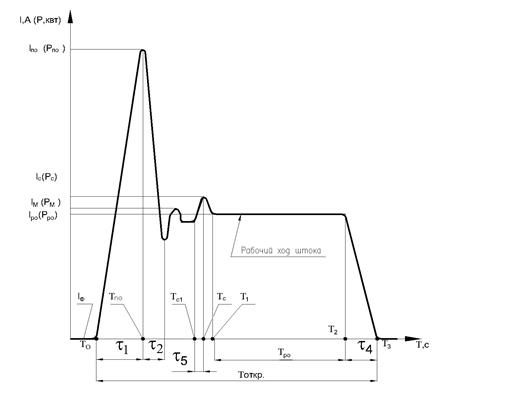
Рисунок 10 – Циклограмма токового сигнала (сигнала активной мощности) при выполнении операции «Открытие»
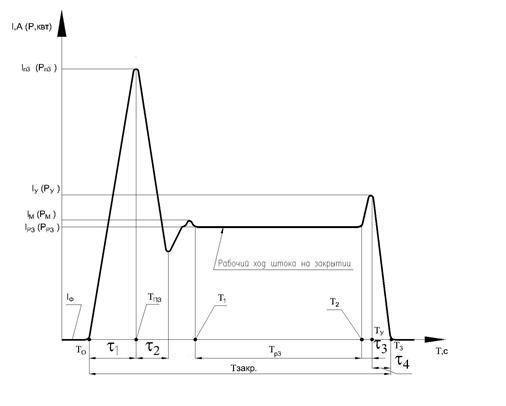
Рисунок 11 – Циклограмма токового сигнала (сигнала активной мощности) при выполнении операции «Закрытие»
Пример выполнения лабораторной работы 3
1. Установим диагностические признаки и для каждого из них укажем нормативный интервал.
Диагностические величины, характеризующие состояние арматуры:
- пусковой ток открытия;
- пусковой ток закрытия;
- ток страгивания;
- ток рабочего хода открытия и закрытия;
- отношение пускового тока к рабочему;
- время открытия/закрытия;
- плавность хода;
- затяг.
По заданным графикам (рис. 2) для каждого из токовых сигналов определим эти показатели и занесем в таблицу 9 для дальнейшей обработки.
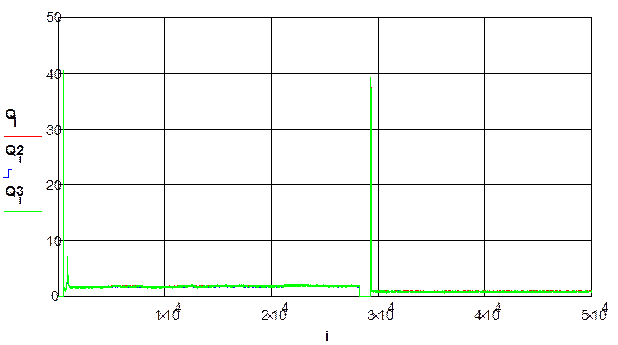 Рисунок 13 - Фаза открытия и подъема клина
Рисунок 13 - Фаза открытия и подъема клина
Таблица 9.
| I0 | Iз | Ic | Ipo | Ipз | I0/Ipo | Iз/Ipз | Iзт | |
| 40,48 | 39,23 | 7,068 | 1,764 | 0,858 | 22,948 | 45,723 | 6,329 | |
| 39,67 | 38,445 | 6,928 | 1,728 | 0,841 | 22,957 | 45,713 | 6,1711 | |
| 40,28 | 39,03 | 6,868 | 1,744 | 0,838 | 23,096 | 46,575 | 6,129 | |
| значение i | 1000-27000 | 30000-56000 | ||||||
| МО | 40,143 | 38,902 | 6, Наши рекомендации
|
