Методические указания по выполнению контрольной работы №2
Задача I.
Вычислить неопределённые интегралы:
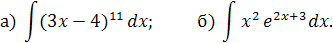
Решение:
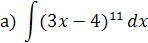
Сделаем замену 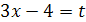 , отсюда
, отсюда 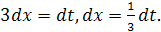
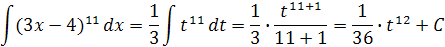
Возвратившись к старой переменной, имеем:
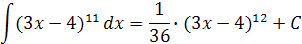
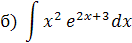
Интегрируем «по частям»: 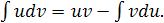
Пусть 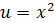 , тогда
, тогда 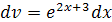
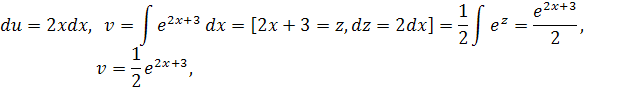
имеем
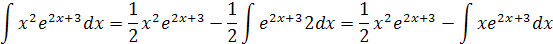
Интеграл 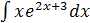 вычислим, снова применяя формулу интегрирования по частям.
вычислим, снова применяя формулу интегрирования по частям.
Пусть 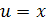 , тогда
, тогда
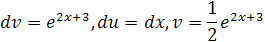
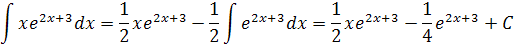
Таким образом, исходный интеграл равен:
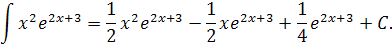
Задача II.
Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертёж области.
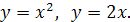
Решение:
Если кривая имеет уравнение 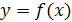 , то площадь, ограниченная этой кривой и отрезком
, то площадь, ограниченная этой кривой и отрезком 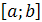 , принадлежащим оси
, принадлежащим оси 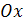 , вычисляется по формуле:
, вычисляется по формуле:
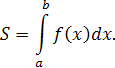
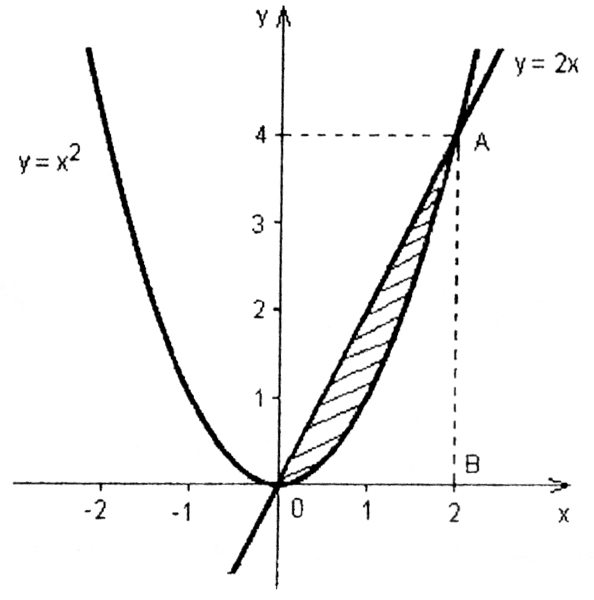
Найдём точки пересечения параболы и прямой:
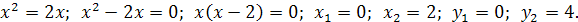
Таким образом, заданные кривые пересекаются в точках 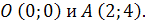 Площадь заштрихованной фигуры можно найти как разность площадей треугольника
Площадь заштрихованной фигуры можно найти как разность площадей треугольника 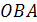 и фигуры, ограниченной кривой
и фигуры, ограниченной кривой 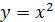 , осью
, осью 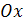 и прямой
и прямой 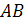 .
.
Следовательно,
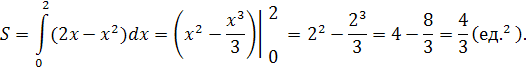
Задача III.
Решить дифференциальное уравнение 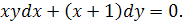
Решение:
Это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, находим общее решение заданного уравнения:
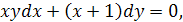
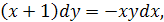
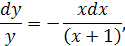
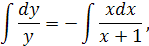
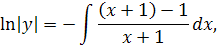
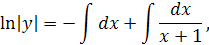
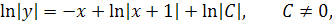
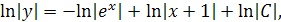
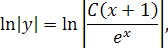
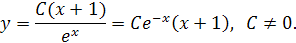
Заметим, что 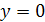 является решением данного уравнения, так что в общем решении можно полагать
является решением данного уравнения, так что в общем решении можно полагать 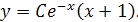
Задача IV. Решить дифференциальное уравнение 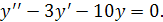
Решение:
Составим характеристическое уравнение. Для этого заменим 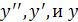 соответственно на
соответственно на 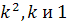 .
.
Характеристическое уравнение имеет вид: 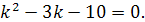
При нахождении решения общего однородного уравнения 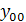 удобно использовать схему:
удобно использовать схему:
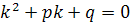 | Решения однородного уравнения |
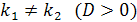 | 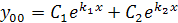 |
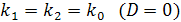 | 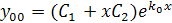 |
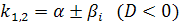 | 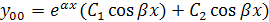 |
Характеристическое уравнение 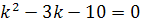 имеет два неравных действительных корня:
имеет два неравных действительных корня:
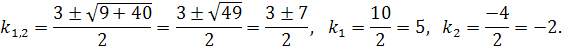
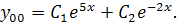
Задача V.
Исследовать на сходимость ряд:
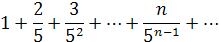
Решение:
Исследовать на сходимость ряд:
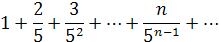
Воспользуемся признаком Д’Аламбера:
Пусть 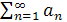 - строго знакоположительный ряд
- строго знакоположительный ряд
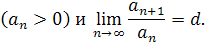
Тогда:
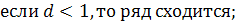
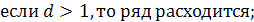
Заметим, что при 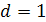 ряд может либо сходиться, либо расходиться, поэтому необходимо дополнительное исследование.
ряд может либо сходиться, либо расходиться, поэтому необходимо дополнительное исследование.
Имеем:
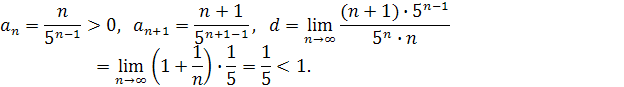
Ряд сходится.
Задача VI.
Решить систему кравнений:
а) методом Крамера,
б) методом Гаусса.
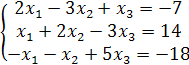
Решение:
а) методом Крамера.
Найдём определители:
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 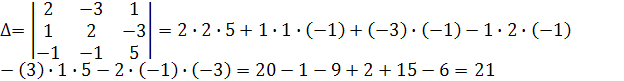
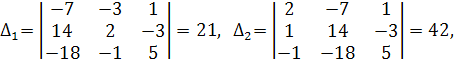
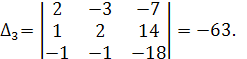
Теперь находим 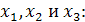
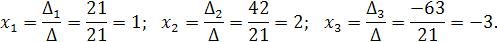
Итак, 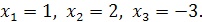
б) метод Гаусса.
Составим расширенную матрицу системы и путём элементарных преобразований приведём данную матрицу системы к треугольному виду (под главной диагональю нули).
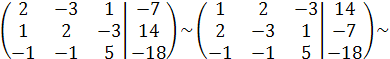
(для упрощения вычислений поменяем местами 1-ю и 2-ю строки; умножим 1-ю строку на –2 и прибавим ко 2-ой строке, 1-ю строку прибавим к 3-ей строке)
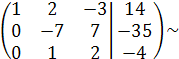
(2-е уравнение разделим на -7)
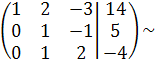
(2-ю строку умножим на –1 и прибавим к 3-ей строке)
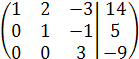
Таким образом, исходная система может быть представлена в виде:
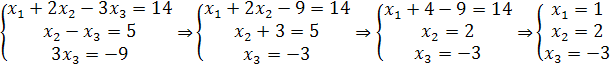
Итак,