Классическая транспортная задача ЛП формулируется следующим образом

Содержание

Содержание 2

Введение 3

Сущность математического метода 4

1 Постановка задачи 4

Разработка основных алгоритмов решения задачи 8

Решение задачи 10

Заключение 19

Список литературы 20

Введение

Тема курсовой работы – открытая модель транспортной задачи.

Транспортная задача является разновидностью линейного программирования. Возникновение и развитие линейного программирования связано с экономикой. В экономике задачи математического программирования, и в частности линейного, возникают в связи с многочисленностью вариантов создания или функционирования определенной экономической системы, с возможностью применения различного сырья, материалов, технологии для производства одной и той же продукции.

Линейное программирование является наиболее развитым и широко используемым на практике разделом математического программирования. Предложение о линейности экономических зависимостей несколько ограничивает возможности линейного программирования, однако простота и наглядность линейных моделей, с достаточной степенью точности описывающих экономические процессы, позволяет применять эти модели в различных видах экономической деятельности.

Основы линейного программирования были заложены советским математиком Л.В. Канторовичем в конце 30-х годов.

В 1949 г. Л.В.Кантоновичем и М.К.Гавуриным предложен новый точный метод для решения транспортной задачи – метод потенциалов. В последующие годы вклад в развитие теории линейного программирования внесли ученые многих стран мира.

Цель данной работы заключается в создании программного продукта для решения задач по теме: «Открытая модель транспортной задачи».

Задачи курсовой работы:

1 изучить теоретический материал по данной теме;

2 изучить методы решения задач;

3 создать алгоритм для решения данной задачи;

4 создать программу для решения задач данного класса.

Программа будет разработана в среде Delphi.

Сущность математического метода

Постановка задачи

Классическая транспортная задача ЛП формулируется следующим образом.

Имеется m пунктов производства (поставщиков) и n пунктов

потребления (потребителей) однородного продукта. Заданы величины:

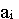- объем производства (запас) i-го поставщика, i=1, m ;

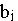- объем потребления (спрос) j-го потребителя, i=1, n ;

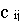- стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос

всех потребителей был бы выполнен и при этом общая стоимость всех

перевозок была бы минимальна.

Математическая модель транспортной задачи имеет вид

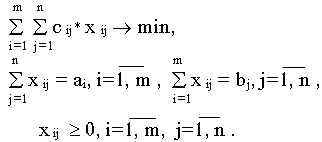
Транспортная задача, в которой суммарные запасы

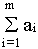
и суммарные потребности

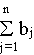
совпадают, называется закрытой моделью; в противном случае - открытой. Открытая модель решается приведением к закрытой.

В случае, когда суммарные запасы превышают суммарные потребности, т.е.

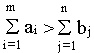
вводится фиктивный n+1 потребитель, потребности которого

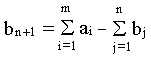
В случае, когда суммарные потребности превышают суммарные запасы, т.е.

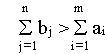
, вводится фиктивный m+1 поставщик, запасы которого

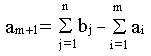
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика

полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к

закрытой модели.

Построение опорного плана транспортной задачи.

Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид: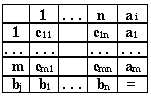

Базисными клетками транспортной таблицы являются клетки с от-

личными от нуля положительными перевозками, остальные клетки - свободные. Базисные клетки образуют опорный план транспортной задачи, если выполняются два условия:

1) сумма перевозок в каждой строке равна запасу 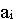в данной

строке;

2) сумма перевозок в каждом столбце равна соответствующему

столбцу спросу

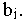
Опорный план транспортной задачи содержит не более n+m-1

отличных от нуля перевозок

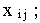
Опорный план называется вырожденным, если число ненулевых перевозок

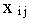
меньше и n+m-1, опорный план - невырожден, если число

ненулевых перевозок равно n+m-1.

Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях.