Сведение матричной игры к задаче линейного программирования

Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом и, наоборот, каждая задача линейного программирования может быть представлена как конечная игра двух лиц с нулевой суммой.

Рассмотрим игру двух лиц с нулевой суммой, заданную платежной матрицей

.

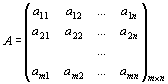Если платежная матрица не имеет седловой точки, т.е. a <b и 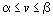, то решение игры представлено в смешанных стратегиях 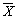(x₁, x₂, ..., x_m) и 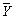(y₁, y₂, ..., y_n).

Применение первым игроком оптимальной стратегии 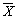_опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры.

, .

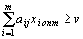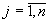Рассмотрим задачу отыскания оптимальной стратегии игрока А, для которой имеют место ограничения

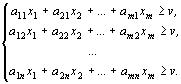
Величина v неизвестна, однако можно считать, что цена игры v > 0. Последнее условие выполняется всегда, если все элементы платежной матрицы неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы некоторое положительное число. Преобразуем систему ограничений, разделив все члены неравенств на v.

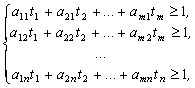(1)

где

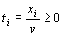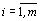, . (2)

По условию x₁ + x₂ + … +x_m = 1. Разделим обе части этого равенства на v.

.

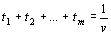Оптимальная стратегия 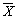(x₁, x₂, ..., x_m) игрока А должна максимизировать величину v, следовательно, функция

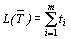(3)

должна принимать минимальное значение.

Таким образом, получена задача линейного программирования: найти минимум целевой функции (3) при ограничениях (1), причем на переменные наложено условие неотрицательности (2). Решая ее, находим значения 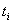, 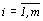и величину1/v, затем отыскиваются значения x_i = vt_i.

Аналогично для второго игрока оптимальная стратегия 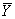_опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры.

, .

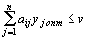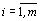Рассмотрим задачу отыскания оптимальной стратегии игрока B, для которой имеют место ограничения

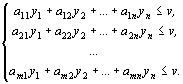
Преобразуем систему ограничений, разделив все члены неравенств на v.

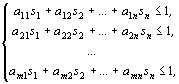(4)

где

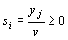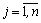, . (5)

По условию y₁ + y₂ + … +y_n = 1. Разделим обе части этого равенства на v.

.

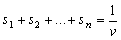Оптимальная стратегия 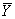(y₁, y₂, ..., y_n) игрока В должна минимизировать величину v, следовательно, функция

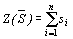(6)

должна принимать максимальное значение.

Получена задача линейного программирования: найти максимум целевой функции (6) при ограничениях (4), причем на переменные наложено условие неотрицательности (5).

Таким образом, для нахождения решения игры имеем симметричную пару двойственных задач линейного программирования. Можно найти решение одной из них, а решение второй находится с использованием теории двойственности.

Пример.Найти решение игры, заданной матрицей

.

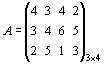a = max (2, 3, 1) = 3, b = min (4, 5, 6, 5) = 4, a ¹ b, .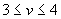

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.

Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования:

,

, .

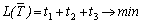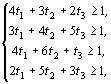
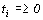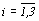Для нахождения оптимальной стратегии игрока В имеем следующую задачу линейного программирования:

,

, .

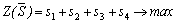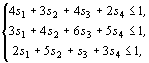
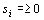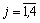Оптимальные решения пары двойственных задач имеют вид

, , .

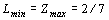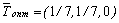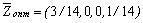Учитывая соотношения между x_i и t_i , y_j и s_j, а также равенство

,

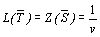можно найти оптимальные стратегии игроков и цену игры:

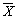(1/2, 1/2, 0), 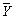(3/4, 0, 0, 1/4), v=7/2.

Игры с природой

В рассмотренных выше матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т. д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.

Условия игры задаются матрицей

.

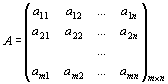Пусть игрок Аимеет стратегии А₁, А₂, …, А_m, а природа – состояния В₁, В₂, …, В_n. Наиболее простой является ситуация, когда известна вероятность p_j каждого состояния природы В_j. При этом, если учтены все возможные состояния, p₁ + p₂ + … + p_j + … + p_n = 1.

Если игрок Авыбирает чистую стратегию А_i , то математическое ожидание выигрыша составит p₁ a_i1 + p₂ a_i2 + … + p_n a_in. Наиболее выгодной будет та стратегия, при которой достигается

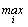( p₁ a_i1 + p₂ a_i2 + … + p_n a_in ).

Если информация о состояниях с природой мала, то можно применить принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы равновероятностны:

,

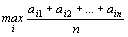т.е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное.

Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.

1. Критерий Вальда. Рекомендуется применять максиминную стратегию. Она выбирается из условия

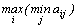
и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека способом.

2. Критерий максимума. Он выбирается из условия

.

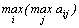Критерий является оптимистическим, считается, что природа будет наиболее благоприятна для человека.

3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

,

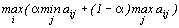где a - степень оптимизма и изменяется в диапазоне [0, 1].

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При a = 1 критерий превращается в критерий Вальда, при a = 0 - в критерий максимума. На a оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем больше последствия ошибочных решений, больше желания застраховаться, тем a ближе к единице.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

.

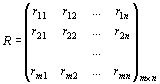Элементы матрицы рисков находятся по формуле

,

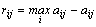где 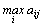- максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия определяется выражением

.

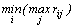При принятии решений в условиях неопределенности следует оценивать различные варианты с точки зрения нескольких критериев. Если рекомендации совпадают, можно с большей уверенностью выбрать наилучшее решение; если рекомендации противоречат друг другу, окончательное решение надо принимать с учетом его сильных и слабых сторон.

Пример. Возможно строительство четырех типов электростанций: А₁ (тепловых), А₂ (приплотинных), А₃ (бесшлюзовых), А₄ (шлюзовых). Состояния природы обозначим через Р₁, Р₂, Р₃, Р₄. Экономическая эффективность строительства отдельных типов электростанций изменяется в зависимости от состояния природы и задана матрицей

.

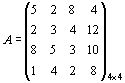1) Согласно критерию Вальда

,

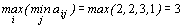следует строить бесшлюзовую электростанцию.

2) Воспользуемся критерием Сэвиджа. Построим матрицу рисков:

.

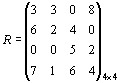Согласно критерию Сэвиджа определяем

.

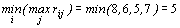В соответствии с этим критерием также предлагается строить бесшлюзовую электростанцию.

3) Воспользуемся критерием Гурвица. Положим a=1/2.

,

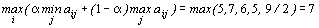т.е. следует принять решение о строительстве приплотинной электростанции.

4) Если принять известным распределение вероятностей для различных состояний природы, например считать эти состояния равновероятностными (р₁=р₂=р₃=р₄=1/4), то для принятия решения следует найти математические ожидания выигрыша:

,

,

,

.

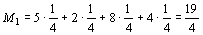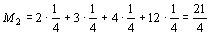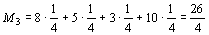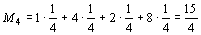Так как максимальное значение имеет М₃, то следует строить бесшлюзовую электростанцию.