Частотные методы оценки качества регулирования
Качество переходных процессов в системах и объектах при гармонических воздействиях оценивают по частотным характеристикам, снятым экспериментально или рассчитанным по параметрам математической модели. В этом случае получают частотные критерии качества переходных процессов, которые относят к косвенным критериям.
Частотные критерии определяют по одной из частотных характеристик: амплитудно-фазовой, амплитудной, вещественной или логарифмической амплитудной.
Различные частотные характеристики замкнутой САУ связаны следующим соотношением:
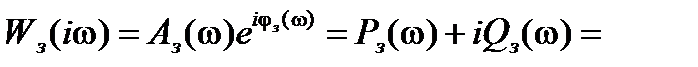
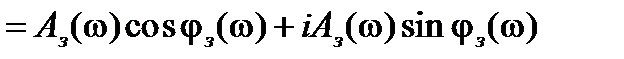 . (15.5)
. (15.5)
Для минимально-фазовых систем, у которых все полюсы и нули передаточной функции имеют отрицательные или равные нулю действительные части, АЧХ и ФЧХ однозначно связаны, поэтому по АЧХ можно определить свойства САУ, в том числе и качество переходных процессов.
По АЧХ (рис. 15.9), в основном, оценивают колебательность и длительность переходной характеристики 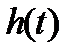 .
.
| wр |
| wсwпрwзпрwгрw |
| A3(w) |
| A3м |
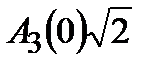 0,707 0,707 |
| А3(0) |
Рис. 15.9 - АЧХ замкнутой САУ
К о л е б а т е л ь н о с т ь определяется по величине относительного максимума АЧХ, называемого показателем колебательности 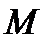 , который является косвенным показателем колебательности САУ :
, который является косвенным показателем колебательности САУ :
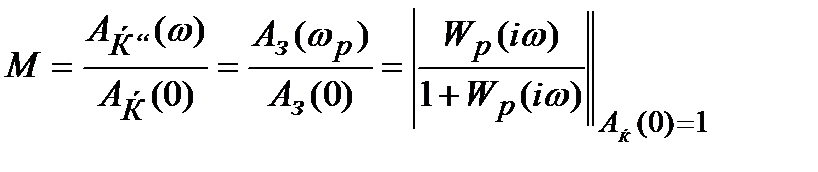 .
.
(15.6)
Например, для колебательной САУ 2-го порядка (кривая 1 на рис. 15.9 ):
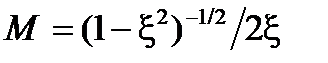 ,
, 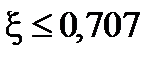 ;
; 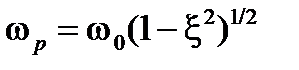 .
.
В случае 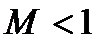 (кривая 2 на рис. 15.9) переходная характеристика системы неколебательна. При
(кривая 2 на рис. 15.9) переходная характеристика системы неколебательна. При 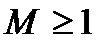 появляетсяколебательность и чем больше
появляетсяколебательность и чем больше 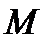 , тем она больше. При
, тем она больше. При 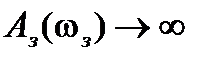
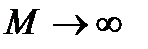 и колебательность возрастает до получения незатухающих колебаний с частотой
и колебательность возрастает до получения незатухающих колебаний с частотой 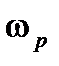 , соответствующих границе устойчивости САУ (пара сопряженных мнимых полюсов
, соответствующих границе устойчивости САУ (пара сопряженных мнимых полюсов 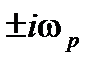 ).
).
Из соотношения 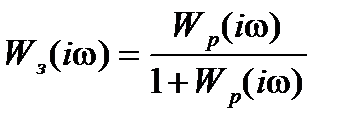 следует, что в диапазоне частот, где
следует, что в диапазоне частот, где
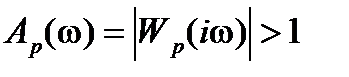
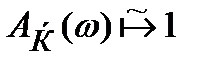 , а
, а 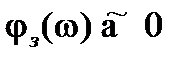 ;
;
при 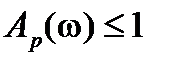
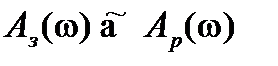 , а
, а 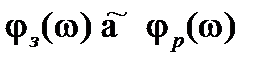 .
.
При 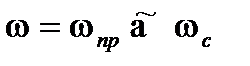
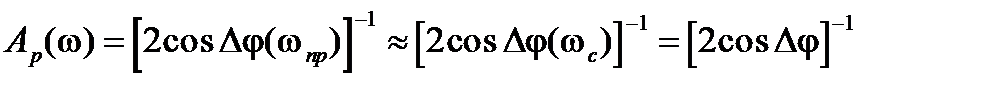 ,
, 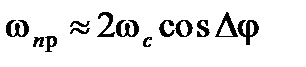 ,
, 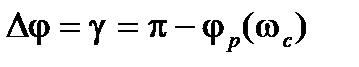 ; максимум
; максимум 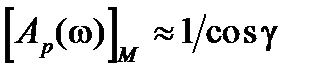 , а
, а 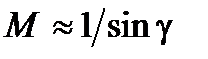 .
.
Обычно рекомендуется 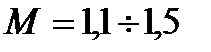 . При этом переходная характеристика имеет слабуюколебательность с частотой, близкой к частоте
. При этом переходная характеристика имеет слабуюколебательность с частотой, близкой к частоте 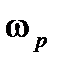 резонансного пика АЧХ с
резонансного пика АЧХ с 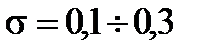 ,
, 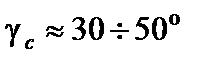 - запас САУ по фазе на частоте среза
- запас САУ по фазе на частоте среза 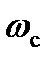 . Допустимо в САУ и значение
. Допустимо в САУ и значение 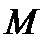 от
от 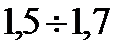 до
до 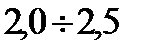 .
.
Д л и т е л ь н о с т ь 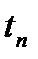 переходной характеристики определяется шириной
переходной характеристики определяется шириной 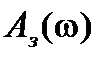 : чем шире АЧХ САУ, тем короче
: чем шире АЧХ САУ, тем короче 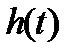 , т.е. меньше
, т.е. меньше 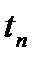 .
.
Длительность 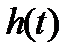 может быть оценена в первом приближении по значению
может быть оценена в первом приближении по значению 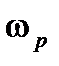 , так как частота колебаний переходной характеристики примерно равна
, так как частота колебаний переходной характеристики примерно равна 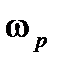 . Учитывая, что время
. Учитывая, что время 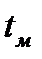 близко к половине периода колебаний этой частоты, можно определить:
близко к половине периода колебаний этой частоты, можно определить:
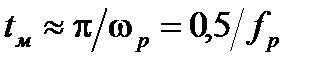 , а
, а 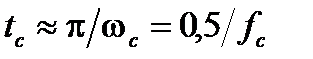 . (15.7)
. (15.7)
Если 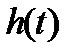 САУ в течение
САУ в течение 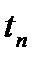 имеет 1¸2 колебания, то
имеет 1¸2 колебания, то 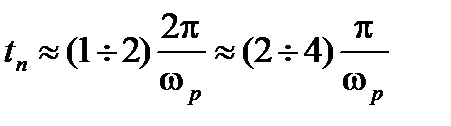 ; так как
; так как 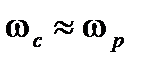 , то
, то 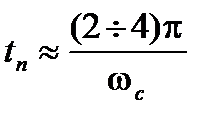 . Для оценки быстродействия САУ используются также частота среза
. Для оценки быстродействия САУ используются также частота среза 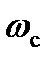 , полоса пропускания САУ
, полоса пропускания САУ 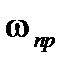 , эквивалентная полоса пропускания САУ
, эквивалентная полоса пропускания САУ 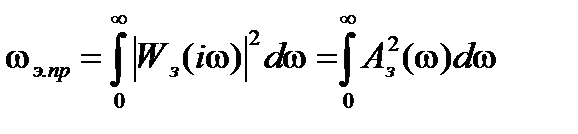 .
.
Колебательность и длительность переходной характеристики замкнутой САУ в первом приближении могут быть оценены непосредственно по параметрам ЛАХ разомкнутой САУ: частоте среза и величинам запасов устойчивости по фазе и амплитуде. В случае колебательной переходной характеристики 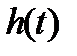 резонансная частота
резонансная частота 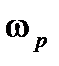 АЧХ замкнутой САУ близка к частоте среза
АЧХ замкнутой САУ близка к частоте среза 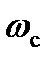 ЛАХ разомкнутой САУ. Поэтому значения
ЛАХ разомкнутой САУ. Поэтому значения 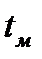 и
и 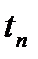 могут быть определены аналогично при подстановке
могут быть определены аналогично при подстановке 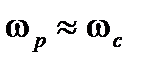 , например в случае неколебательной
, например в случае неколебательной 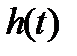 ,
, 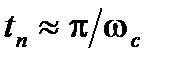 .
.
Колебательность считается допустимой, если ЛАХ на частоте среза 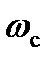 имеет наклон в минус 20 дБ, чем шире участок с таким наклоном, тем меньше колебательность. При ширине этого участка около одной декады и нахождении
имеет наклон в минус 20 дБ, чем шире участок с таким наклоном, тем меньше колебательность. При ширине этого участка около одной декады и нахождении 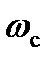 ближе к его концу перерегулирование в САУ не будет превышать 20-30 %. Если запас по фазе
ближе к его концу перерегулирование в САУ не будет превышать 20-30 %. Если запас по фазе 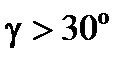 , запас по амплитуде минус 6 дБ, то
, запас по амплитуде минус 6 дБ, то 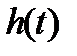 имеет слабую колебательность.
имеет слабую колебательность.
В силу соотношения (15.5) колебательность и длительность переходного процесса могут быть определены по вещественной (действительной) частотной характеристике (ВЧХ) 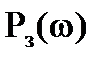 замкнутой САУ.
замкнутой САУ.
Детальные и более точные зависимости, связывающие показатели качества системы с частотными характеристиками, имеются в учебной и справочной литературе по ТАУ. Для познания сути вопроса важны следующие выводы.
1. Близкие по форме АЧХ и ВЧХ САУ имеют близкие по качеству переходные процессы.
2. Частота 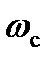 определяет быстродействие САУ, т.е. чем больше
определяет быстродействие САУ, т.е. чем больше 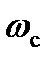 , тем меньше
, тем меньше 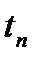 . Но при значительных
. Но при значительных 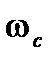 вместе с полезным сигналом проходят и помехи, поэтому не следует стремиться делать
вместе с полезным сигналом проходят и помехи, поэтому не следует стремиться делать 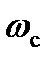 чрезмерно большой.
чрезмерно большой.
3. Наличие пика в АЧХ ( 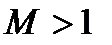 ) и ВЧХ говорит о колебательности САУ.
) и ВЧХ говорит о колебательности САУ.
4. Если в АЧХ или ВЧХ САУ имеется разрыв на определенной частоте 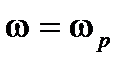 , то в САУ на этой частоте возникают незатухающие колебания (САУ находится на колебательной границе устойчивости).
, то в САУ на этой частоте возникают незатухающие колебания (САУ находится на колебательной границе устойчивости).
5. Если АЧХ или ВЧХ имеет разрыв при 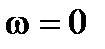 , то в САУ имеет место апериодическая граница устойчивости.
, то в САУ имеет место апериодическая граница устойчивости.
6. Острый пик АЧХ или ВЧХ при 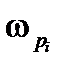 говорит о сильной колебательности с частотой, близкой к
говорит о сильной колебательности с частотой, близкой к 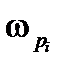 и значительном
и значительном 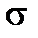 .
.
7. С увеличением 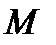 возрастают
возрастают 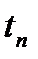 ,
, 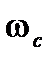 ,
, 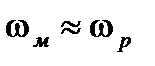 ,
, 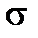 и уменьшается
и уменьшается 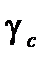 ; следовательно, увеличение
; следовательно, увеличение 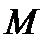 ведет к ухудшению качества САУ.
ведет к ухудшению качества САУ.
8. Оценки качества переходных процессов в общем случае могут быть определены по соответствующим характеристикам разомкнутой САУ, благодаря связи АЧХ и ФЧХ замкнутой и разомкнутой САУ.
Изложенное выше относится к минимально-фазовым системам; однако в первом приближении рассмотренные оценки качества переходных процессов могут быть применены и к неминимально-фазовым системам. При этом погрешность тем больше, чем больше различаются ФЧХ САУ.
Особые частоты: ω+ – граница интервала частот положительности ВЧХ, ω0 – частота собственных колебаний, ωсущ – граница интервала существенных частот, вне которого текущее значение функции уже не превышает (0,05…0,1)P(0).
Общие принципы оценки качества по вещественной частотной характеристике P(ω):
- P(0) = h(∞) = kуст – конечное значение переходной характеристики численно равно начальному значению ВЧХ;
- P(∞) = h(0) – начальное значение переходной характеристики численно равно конечному значению ВЧХ;
- a·P(ω) ÷ a·h(t) – кратность изменения масштаба ВЧХ и переходной характеристики одинакова;
- P(a·ω) ÷ h(t/a) – расширение полосы рабочих частот ведет к соразмерному повышению быстродействия системы;
- время регулирования π/ω+<tрег<4π/ω+,
- перерегулирование σ определяется по форме ВЧХ:
а) если ВЧХ монотонно убывает, то перерегулирование σ = 0;
б) если ВЧХявляется положительной невозрастающей функцией, то перерегулирование σ < 18 %;
в) если ВЧХ имеет подъем от P(0), то 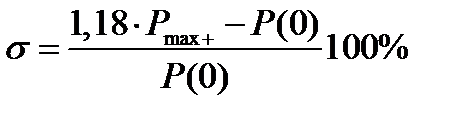 ;
;
г) если ВЧХ имеет отрицательный минимум со значением более 0,1P(0), то с его учетом 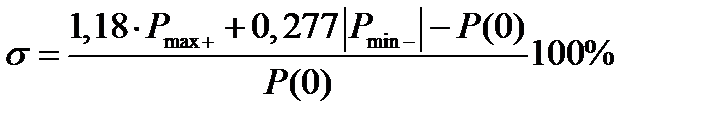 ;
;
д) если ВЧХ терпит разрыв при ω=ω0, система совершает незатухающие колебания, tрег→ ∞ и показатели качества не определяются.
При оценке качества регулирования по АЧХ обычно вычисляют значение частотного показателя колебательности, равное отношению максимума характеристики к ее начальному значению М = Ам/А(0). При М = 1 переходная характеристика системы не колебательна, при М → ∞ система находится на границе устойчивости, наблюдаются незатухающие колебания с частотой ω0. Оптимальными считаются значения М = 1,1..1,5, которым соответствует перерегулирование 10-30 % и запас по фазе 30-50°.
Пример 1. Оценить значение частотного показателя колебательности системы по её АЧХ (рисунок 15.8).
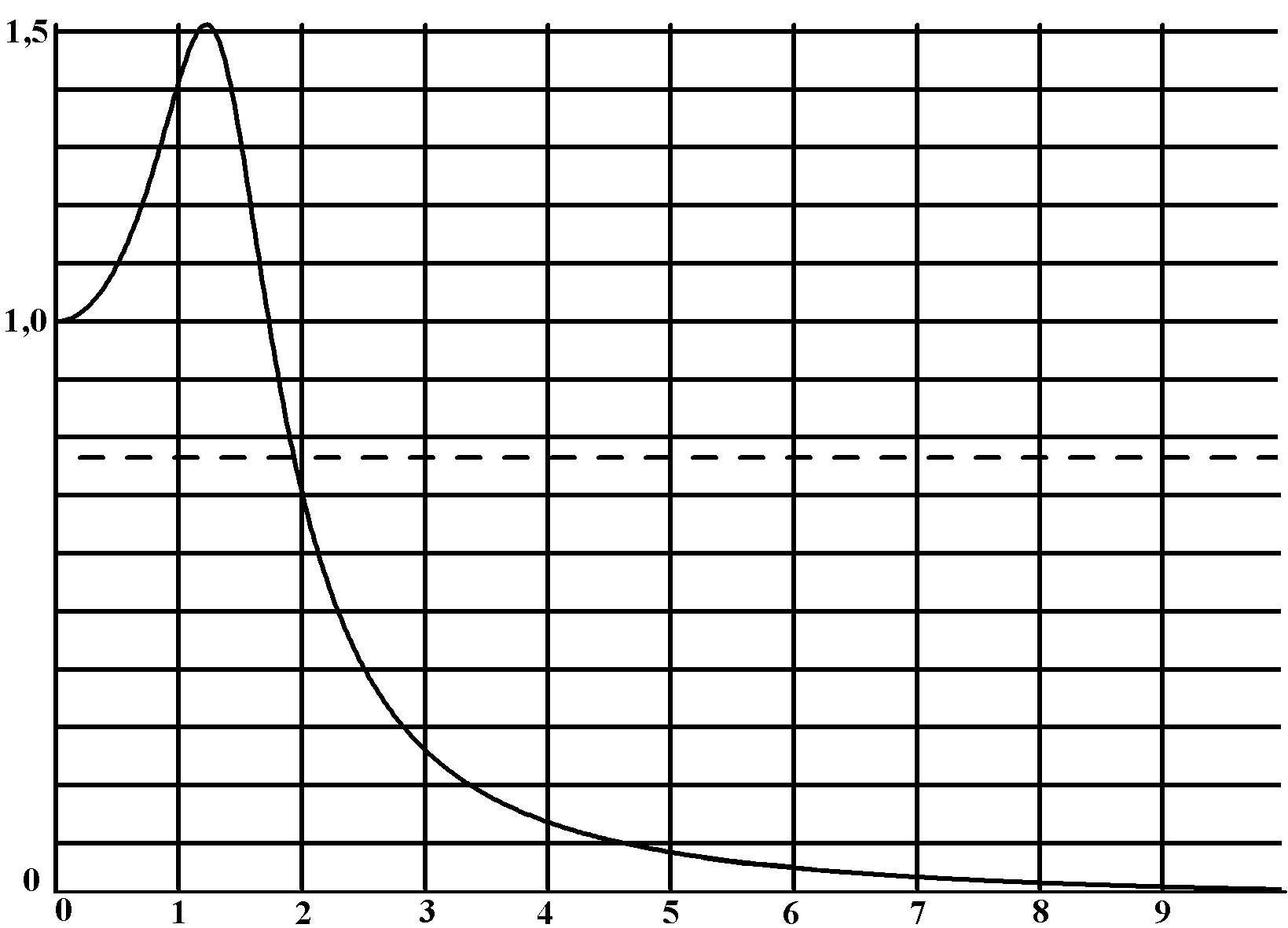
Рисунок 15.8
Максимальное значение АЧХ равно 1,51, следовательно, показатель колебательностиМ = 1,51/1,0 = 1,51, что ещё удовлетворяет минимальному запасу по фазе 30° и перерегулированию 30 %.
Пример 2. Найти значение перерегулирования и времени регулирования системы по заданной АФЧХ (рисунок 15.9)
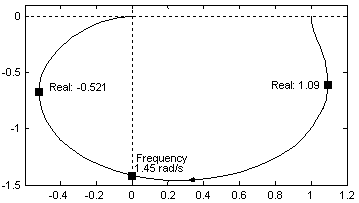
Рисунок 15.9
Частота ω+ = 1,45 рад/с, положительный максимум ВЧХ равен 1,09 при начальном значении Р(0) = 1,0, отрицательный минимум 0,521. Отсюда получаем перерегулирование
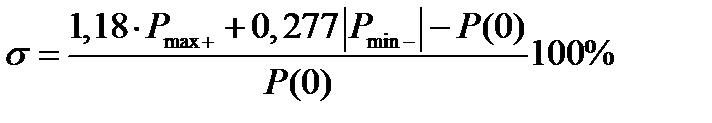 =
=
= (1,18*1,09 + 0,277*0,521 – 1,0)*100 = 43,1 %
и время регулирования не более 4π/ω+ = 4*3,1415926/1,45 = 8,67 с.
Указания по выполнению работы
С помощью частотного метода определить показатели качества переходных процессов для линейной системы автоматического управления со следующей структурной схемой при K = 10; Т = 0,2с.
Решение
Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.
