II. Векторная алгебра и аналитическая геометрия

I. Линейная алгебра.

1. Вычислить

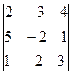= б) -10

2. Дана матрица А = 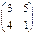. Найти 2А+5 = в)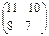

3. Система линейных уравнений называется несовместной, если = б) не имеет ни одного решения

4. Дана матрица А = 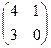. Найти А². = б)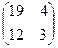

5. При перестановке двух столбцов величина определителя: в) меняет свой знак на противоположный

6. Найти произведение матриц А*В, где А = (2 4 0), В = 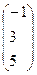. = б) (10)

7. Дана матрица А = 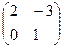. Найти А². = б)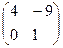

8. Найти алгебраическое дополнение А₂₁ матрицы А = 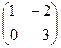. = в) 2

9. Найти обратную матрице А = 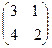. = в)

10. Единичной матрицей является матрица: = в)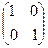

11. Дана матрица А = 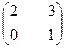. Найти А². = а)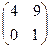

12. Величина определителя не изменится от: = в) транспорирования

13. Вычислить определитель 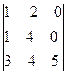. = б) 10

14. Найти произведение матриц: А = (1 0 2); В = 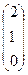. = в) 2

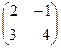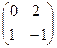15. Дана матрица А = , В = , Найти АВ. = б)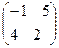

16. Дана матрица А = 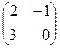.Найти А₁₂. = г) -3

17. Если матрица В является обратной к матрице А то: = а) АВ=Е

18. Решение матричного уравнения ВХ = А ищем в виде: = в) Х=В^-1А

19. Если размеры матриц А и В соответственно равны

(3 × 4) и (4 × 5), то размеры С = А · В равны = г) (3 × 5)

20. Складывать можно только матрицы = б) одинаковых размеров

21. Умножать можно только матрицы = г) размерами А(m*n), В(n*l)

22.Вычислить определитель

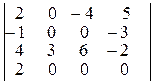= д) -72

23. Найти матрицу 3А, если 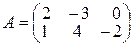= а)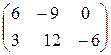

24. Найдите произведение матриц 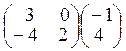= в)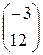

25. Найдите ранг матрицы 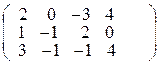= б) 2

26. Найдите А^-1 , если 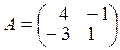= г)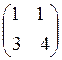

26. Чему равен ранг единичной матрицы четвертого порядка = г) 4

27. Решите систему линейных уравнений

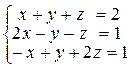в) (1;0;1)

29. Решите систему линейных уравнений

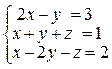д) (с; 2с – 3; -3с + 4)

30. Решите систему линейных уравнений

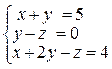= б) не совместна

31. Решите систему линейных однородных уравнений

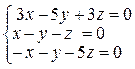= в) (0;0;0)

32. Если 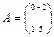,то значение многочлена f(x)=5x+2 от матрицы А есть = в)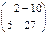

33. Указать размер матрицы – произведения С

А(2,3)В(3,3)=С = а) 2,3

34. Алгебраическое дополнение А₃₂ определителя 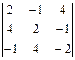равно = г) 18

35. При перестановке двух строк, величина определителя: = в) меняет свой знак на противоположный

II. Векторная алгебра и аналитическая геометрия.

1. Определить угол между векторами:

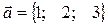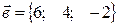, . = в) φ = arcos(2/7)

2. Найти векторное произведение векторов

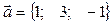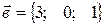, . = а)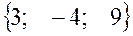

3. Дана прямая 5х + 3у – 3 = 0. Определить угловой коэффициент к прямой, перпендикулярной данной. = в) 3/5

4. Найти проекции вектора 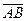на координатные оси, если:

А(3; -1; 2); В(2; 1; -3). = в)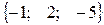

5. Скалярное произведение векторов 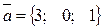, 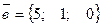равно = а) 15

6. В пространстве уравнений у = х² определяет: = г) цилиндр

7. На плоскости уравнение у = 2х – 1 определяет: = а) прямую

8. Прямая 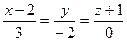и плоскость 6х – 4y + 5 = 0 образуют угол: = а)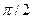

9. Указать название следующей поверхности х² + у² = z². = а) конус

10. Уравнение прямой, проходящей через две точки А(-1; 2; 3), В(2; 6; -2) имеет вид:

= б)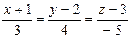

10. Угол между прямыми 2х + у = 0, у = 3х – 4 равен: = в) 45⁰ (или -45)

12. Указать название линии заданной уравнением х² + у² = 2х. = г) окружность

13. Кривизна прямой у = 7х + 8 в точке х₀ = 1 равна: = б) 0

14. Что определяет уравнение х² + у² = 4 в пространстве? = б) круговой цилиндр

15. Корнями уравнения х² + 4х + 13 = 0 являются = б) -2±3i

16. Выполнив действие 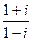, получим = б) i

17. Найти i⁷ = г) - i

18. Найти (1 + i)² + (1 – i)² = а) 0

19. Найти алгебраическую форму комплексного числа z = 2е^-ip/2. = г) -2i

20. Уравнение плоскости, проходящей через т. М(-1,3,0) и перпендикулярной

вектору 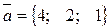, имеет вид: = а) 4х + 2у + z – 2 = 0

21. Прямые 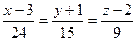и 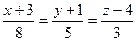= б) параллельны

22. Найти точку пересечения двух прямых 3х – 4у – 29 = 0 и 2х + 5у + 19 = 0 = г) (3;-5)

23. Какую кривую определяет уравнение (х – 2)² + (у – 4)² = 25 на плоскости? = д) окружность

24. Уравнение 4z = х² + у² задает в пространстве: = в) параболоид

25. Найти векторное произведение векторов 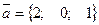, 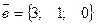= б)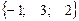

26. Уравнение прямой, параллельной прямой у = 2х + 1 и проходящей через точку (1;1) будет: = г) у = 2х – 1

27. Уравнение плоскости, проходящей через точку М(1;2;0) и перпендикулярной вектору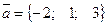

будет: = а) 2х – у – 3z = 0

28. Прямые 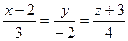и 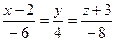= а) параллельны

29. Уравнение х²/3 + у²/2 + z²/4 = 1 задает в пространстве = г) эллипсоид

Уравнение х – у + 1 = 0 задает на плоскости: прямую

Установите соответствие 1Б, 2А, 3Г, 4В

Уравнение Названия (на плоскости)

1) х + у + 5 = 0 А) парабола

2) у = х² Б) прямая

3) z² + у² = 4 В) гипербола

4) z² - у² = 1 Г) окружность

30. Установите соответствие г) 1В, 2Д, 3Г, 4Б, 5А,

Уравнение Названия (в пространстве)

1) х + у + 5 = 0 А) прямая

2) у = х² Б) конус

3) z² + у² = х В) плоскость

4) z² + у² = х² Г) параболоид

5) х/2 = у/3 = z/4 Д) цилиндр.

31. Угол между прямыми в пространстве

х = 2t – 1 и х = 4t – 1

у = -t + 2 у = -2t + 2 равен:

z = 3t z = 6t = а) 0

32. Вычислить (1 – i) (1 + i) = г) 2.

33. Записать показательную форму комплексного числа Z = -1 + 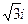= в)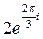

34. Квадратное уравнение х² + 2х + 5 = 0 имеет корни = а) -1 ± 2i

35. Найти скалярное произведение векторов 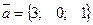, 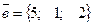. = в) 17

36. Прямая 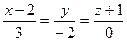и плоскость 2х + 3у + 5z = 0 образуют угол = 0

37. Угол между прямыми на плоскости у = 2х + 1 и у = 2х – 1 равен = 0

38. Установите соответствие = д) 1Б,2В,3Г,4А.

Уравнение Кривая

1) х²/а² + у²/в² = 1 А) прямая

2) х²/а² - у²/в² = 1 Б) эллипс

3) у² = 2рх В) гипербола

4) Ах + Ву + С =0 Г) парабола.

39. Две прямые в пространстве

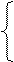
х = 2t – 1 и х = 4t – 1

у = -t + 2 у = -2t + 2 б) параллельны

z = 3t z = 6t

40. Какая из плоскостей параллельна координатной плоскости Z = 0? = в) z = 5

41. Вычислить i⁹⁸ = г) -1

42. Записать тригонометрическую форму комплексного числа Z = 1+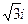

= б) Z = 2(cos(p/3)+isin(p/3))

43. Квадратное уравнение х² + 4х + 5 = 0 имеет корни: = а) -2 + i; -2 – i

44. Расстояние между точками А(-5;0) и В(-12;0) равно = б) 7

45. Уравнение плоскости, проходящей через точки А(2;0;0), В(0;4;0),С(0;0;8)

имеет вид б)4x+2y+z-8=0

46. Направляющий вектор прямой 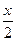= у = -z имеет координаты = г) (2;1;-1)

47. Уравнение х²-у²=1 определяет на плоскости хоу = б) гипербола

48. Расстояние между точками А(-5;0) и В(12;0) равно = г)17

49. Найти длину вектора `а-`в, если `а=(1;-2;3) `в=(-1;0;2) = б) 3

50. Найти скалярное произведение векторов`а и `а+`в если `а=(1;2;0) `в=(0;-1;3) = а)=3

у

51.По графику прямой написать ее уравнение = в)2х+3у-6=0

52. Уравнение окружности с центром в точке С(1;2), проходящей через точку М(3;4) имеет вид = в) (х-1)²+(у-2)²=8

53.Уравнение плоскости, проходящей через точки А(0;0;0), В(0;4;0), С(0;0;8) имеет вид = д) x = 0

54.Уравнение прямой, проходящей через точки А(-1;2;3) В(2;6;-2) имеет вид

= г) = =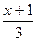

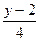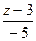
55.Направляющий вектор прямой 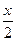= у = z имеет координаты = в) (2;1;1)

56.Направляющий вектор прямой х=4t-1, y=6t+4, z=5 имеет координаты = г) (4;6;0)

57.Выяснить: как расположена прямая x = t, y = 2t-1, z=3 относительно плоскости = б) параллельна плоскости

58.Уравнение х²+у²=6у определяет на плоскости окружность

59.Уравнение х²-у²=1 определяет на плоскости хоу гиперболу

60.Уравнение у²= -6х определяет на плоскости хоу параболу, симметричную оси ОХ