Изучение вынужденных колебаний

В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ

Цель работы: изучение вынужденных колебаний в электрическом контуре и определение параметров контура.

1. Теория

Рис. 1.

Колебания, в процессе которых колебательная система подвергается внешнему периодически изменяющемуся воздействию, называются вынужденными колебаниями. В электрическом колебательном контуре внешнее воздействие обычно обусловлено подключением к контуру внешней периодически изменяющейся со временем электродвижущей силы E(t), которая создает в контуре переменное электрическое напряжение (рис.1). 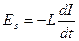Уравнение Кирхгофа (на основе второго правила Кирхгофа) с учетом внешней ЭДС E(t) и ЭДС самоиндукции , возникающей в катушке индуктивности L, имеет вид:

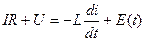(1)

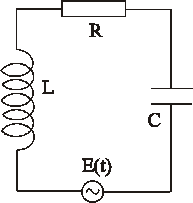
Здесь I – сила тока в цепи, R – электрическое сопротивление, U – напряжение на конденсаторе, L – индуктивность. С учетом того, что ток 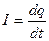, а напряжение 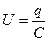, уравнение (1) может быть преобразовано к следующему виду:

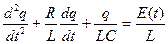(2)

с учетом обычно применяемых обозначений 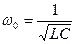(собственная частота колебательного контура) и 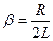, уравнение (2) можно переписать в виде:

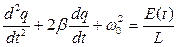(3)

Рассмотрим случай, когда к контуру подключается ЭДС E(t), изменяющаяся гармонически:

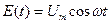(4)

Общее решение уравнения (3) с учетом (4) имеет вид:

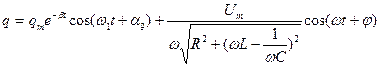(5)

Первое слагаемое описывает затухающие колебания и убывает с течением времени, т.к. содержит множитель 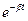. При анализе установившихся колебаний 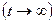первым слагаемым можно пренебречь, т.к. оно стремится к нулю. Следовательно, установившиеся колебания описываются вторым слагаемым выражения (5). Т.е. заряд и напряжение на конденсаторе при установившихся колебаниях будут определяться соотношениями:

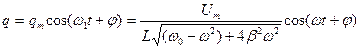(6)

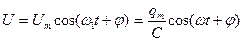, (7)

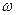т.е. вынужденные колебания происходят с частотой равной частоте внешней ЭДС, а амплитуда колебаний зависит от этой частоты. Резкое возрастание амплитуды колебаний при приближении частоты внешнего воздействия к собственной частоте колебательной системы 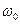называется резонансом. В общем случае резонансная частота не совпадает точно с собственной частотой колебательной системы. Значение резонансной частоты рассчитывается путем поиска минимума выражения, стоящего в знаменателе (6). Для этого нужно взять производную от выражения стоящего под корнем в знаменателе (6) и приравнять ее нулю:

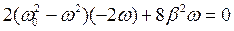(8)

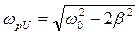(9)

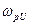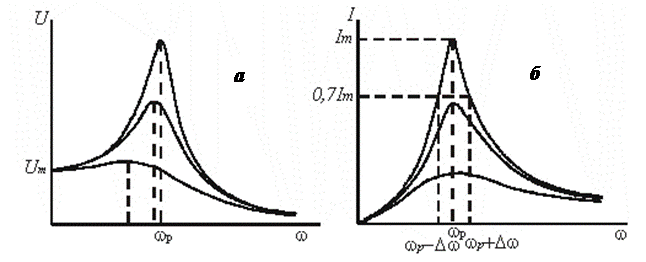
Из (9) следует, что резонансная частота для напряжения меньше собственной частоты контура 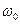.График зависимости амплитуды колебаний от частоты внешней ЭДС называют резонансной кривой. Резонансные кривые для U изображены на рис. 2а. При 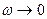кривые сходятся в одной точке с ординатой U_m, равной напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения U_m. Максимум при резонансе получается тем выше и острее, чем меньше коэффициент 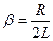, т.е. чем меньше активное сопротивление 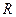и больше индуктивность .

		Рис. 2.

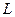Пик на резонансной кривой напряжения, соответствующий частоте 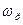, указывает на наступление резонанса. Величина активного сопротивления контура 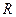определяет максимальное значение тока в контуре при наступлении резонанса. На графике это проявляется в изменении высоты и остроты “пика” на резонансной кривой. Вид резонансной кривой, т.е. зависимость амплитуды вынужденных колебаний от частоты внешней ЭДС, определяет, как быстро в контуре происходит затухание колебаний, имеющих частоту, отличающуюся от резонансной. Сила тока в контуре при установившихся колебаниях равна:

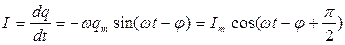(10)

где 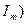– амплитуда тока,

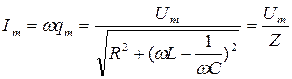
а выражение

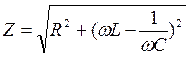
называют полным электрическим сопротивлением или импедансом. Максимальное значение амплитуды тока достигается при условии 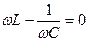. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура :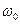

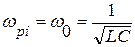(11)

ри частоте 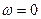сила тока в контуре равна нулю, т.к. при постоянном напряжении ток в цепи с конденсатором течь не может. Резонансные кривые для силы тока изображены на рис.2б. Чем уже резонансная кривая, тем выше избирательность колебательного контура, т.е. способность контура выделить определенную частоту из многих сигналов различной частоты. Избирательность контура принято характеризовать полосой пропускания. Под полосой пропускания контура понимают ширину резонансной кривой, выраженную в Герцах и определенную по уровню 0,7 от максимальной амплитуды колебаний (см. рис.2). Следует отметить, что добротность контура может быть определена по виду резонансной кривой по формуле:

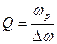(12)

где 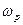– резонансная частота, 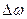– полоса пропускания контура.

2. Задания и порядок выполнения работы.

1. Изучить теорию работы, разобраться в устройстве лабораторного стенда и методике измерений.

2. Генератор ГЗ-106 подключить к лабораторному стенду, включить и настроить на частоту выходного сигнала 10 кГц с амплитудой примерно 1 В.

3. Изменяя емкость переменного конденсатора колебательного контура добиться резонанса в контуре (отыскав положение ручки настройки при котором сигнал, наблюдаемый на осциллографе имеет максимальное напряжение). При этом собственная частота колебаний в контуре окажется равной частоте внешнего сигнала, т.е. 10 кГц.

4. Изменяя частоту генератора ГЗ-106 в диапазоне от 5 до 15 кГц, снять резонансные кривые для исследуемого контура при различных значениях активного сопротивления .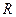

5. С помощью осциллографа измерить амплитудные значения напряжений в контуре при резонансе. Вычислить индуктивность контура воспользовавшись формулой Томсона: 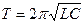, взяв емкость конденсатора по шкале стенда и учитывая, что 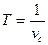, где 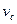– собственная частота контура.

6. Построить на графике резонансные кривые и определить по ним полосу пропускания контура в различных режимах (при разных значениях активного сопротивления). Рассчитать добротность контура по формул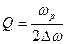е , где 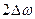– полоса пропускания контура.

7. Рассчитать волновое сопротивление контура по формуле: .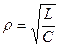

Контрольные вопросы.

1. Что такое резонанс? При каких условиях он наблюдается?
2. Что такое полоса пропускания контура и как можно определить ее экспериментально?
3. Где и для чего может применяться колебательный контур?
4. Что называется импедансом контура?
5. Что такое вынужденные колебания? В чем разница между свободными и вынужденными колебаниями?

Литература