Дискретизация дифференциальных уравнений

В частных производных

Решением дифференциального уравнения называется функция непрерывного аргумента, обращающая это уравнение в тождество при заданных граничных и начальных условиях. При численном решении исходное дифференциальное уравнение (вместе с граничными и начальными условиями) заменяется эквивалентной системой алгебраических уравнений, а численным решением называется сеточная функция, обращающая указанную систему алгебраических уравнений в тождество.

Процесс замены дифференциального уравнения системой алгебраических уравнений называется дискретизацией, а сама алгебраическая система – дискретным аналогом дифференциального уравнения. Цель наших дальнейших действий заключается в изучении широко распространенных способов получения (построения) дискретных аналогов дифференциальных уравнений в частных производных.

4.1 Метод конечных разностей

Введенное в предыдущем параграфе определение сеточной функции естественным образом распространяется на случай двух и более аргументов. Простейшую двумерную сетку {x_i,j, y_i,j} можно построить как набор из J одномерных сеток, каждая из которых содержит I узлов, при этом должно выполняться условие:

xi-1, j< xi, j< xi+1, j ; yi, j-1< yi, j< yi, j+1

(19)

Очевидно, что суммарное число сеточных узлов в этом случае будет I×J. Расчетные сетки, удовлетворяющие условию (19), называются регулярными (упорядоченными). Для упрощения записи в дальнейшем мы будем использовать обозначение Ф_i,j= 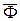(х_i,j, у_i,j). Пример сеточной функции двух переменных, построенной на регулярной сетке, приведен на рис. 5.

Рис. 5. Сеточная функция двух переменных, заданная на упорядоченной сетке

Частные производные функции могут быть аппроксимированы аналогично (9). Например, в случае Δx=const, Δy=const[19] при использовании центрального конечно-разностного отношения, будем иметь:

, , , ,

(20)

Продемонстрируем применение метода конечных разностей на примере нестационарного уравнениятеплопроводности (уравнение диффузии):

,

(21)

где Т – температура (подлежащая определению в результате решения), t – время, α – коэффициент теплопроводности, х – координата.

С точки зрения физики, уравнение (21) описывает нестационарный процесс распространения тепла в стержне с теплоизолированной боковой поверхностью и возможностью подвода (отвода) теплоты на его торцах (рис. 6).

С математической точки зрения, решением уравнения (21) является функция, зависящая от двух переменных (координата х и время t).

Рис. 6. Стержень с теплоизолированной боковой поверхностью

Для решения задачи должно быть заданы:

§ граничное условие на левом торце стержня – либо зависимость температуры от времени T₀=T(x₀,t) (условие Дирихле) либо пространственная производная (условие Неймана);

§ граничное условие на правом конце стержня – T_N=T(x_N,t) либо ;

§ начальное условие – закон распределения температуры по всей длине стержня в начальный момент времени Т(х, 0), где x₀<x< x_N.

Заменим[20] производную по времени в уравнении теплопроводности (21) разностным отношением вперед (см. 9b), а вторую производную по пространственной координате – центральным конечно-разностным отношением (см. 20)[21]:

,

(22)

где i – номер рассматриваемого сеточного узла, j – номер рассматри­ваемого шага по времени, Δx – шаг пространственной сетки, Δt – шаг по времени, T_i,j – температура в сеточном узле с координатой x_i=x₀+i∙Δx в момент времени t_j= j∙Δt.

Схема используемой расчетной сетки приведена на рис. 7. На рис. 8а приведен фрагмент расчетной сетки (расчетный шаблон, расчетная схема), включающий в себя только те узлы сетки, которые "упоминаются" в уравнении (22).

Рис. 7. Расчетная сетка, используемая для решения уравнения теплопроводности (21)

а) явная схема

б) неявная схема

Рис. 8. Расчетные шаблоны, используемые для решения уравнения теплопроводности

Алгебраическое уравнение (21) позволяет методом "последовательного обхода" узлов расчетной сетки найти все неизвестные значения сеточной функции T_{i, j}:

,

(22a)

Как следует из рассмотрения рис. 8а, в правой части уравнения (22a) упоминаются лишь те узлы расчетной сетки, значения температуры в которых уже известны. Расчетные схемы, обладающие указанным свойством, называются явными. Данное обстоятельство, с одной стороны, существенно упрощает решение задачи об отыскании значений сеточной функции Т_{i, j}, с другой стороны, анализ формулы (22a), показывает, что температура в узле x_i в момент времени t_j+1, зависит только от температуры в узлах x_i-1, x_i, x_i+1 в момент времени t_j, и не зависит от распределения температур внутри стержня в момент времени t_j+1, что не вполне соответствует физическому смыслу задачи.

Для устранения этого противоречия, несколько видоизменим аппроксимацию производной в уравнении (21):

,

(23)

или:

.

(23a)

Правая часть уравнения (23a) содержит неизвестные величины T_i-1,j+1 и T_i+1,j+1, поэтому оно не может быть непосредственно (без увеличения объема вычислительной работы) использовано для нахождения температуры T_i,j+1. Расчетный шаблон для неявной расчетной схемы (23a) приведен на рис. 8б. Как показывают оценки [Флетчер], объем вычислений, при применении неявной схемы вместо явной схемы (22a), возрастает, ориентировочно, в два раза. Однако лучшая физическая обоснованность неявной схемы позволяет нам рассчитывать на более высокое качество результатов расчета.

В качестве примера, обсудим решение неявного уравнения (23а) методом итераций(Гаусса-Зейделя). Первый этап метода заключается в выборе начального приближения для искомых значений функции. В данном случае, хорошей идеей представляется использование в качестве начального приближения значений температуры, взятых с предыдущего временного слоя, т.е.

, для всех[22] i=1 … N-1

(24)

где верхний индекс означает номер итерации.

Тогда, с учетом (23а), в первом приближении температура в момент времени t_j+1 может быть определена как

, , …, .

(25)

Скорее всего, значения температуры, определенные в первом приближении, не будут удовлетворять исходному уравнению (23). Поэтому процесс придется продолжать до тех пор, пока для каждого узла сетки различие между результатами, полученными на очередной и предыдущей итерациях, не станет меньше некоторой наперед заданной величины (точности решения) ε, т.е. пока не будет выполнено условие:

, для всех i=1 … N-1.

(26)

Следует также предусмотреть прекращение расчета в том случае, если решения не удастся достигнуть (решение не сойдется) после некоторого "разумного" числа итераций К. Причиной отсутствия сходимости, в частности, могут стать завышенные требования к точности решения ε, чрезмерно большие шаги расчетной сетки Δx и Δt, неудачный выбор начального приближения, а также некоторые физические эффекты[23].

В некоторых случаях, добиться сходимости решения удается за счет использования метода релаксации. Преобразуем последнюю из формул (25) к виду:

,

(25а)

где r – коэффициент релаксации (r>0).

Очевидно, что, при r=1, формула (25а) совпадает с последней из формул (25). При значениях 0<r<1 (нижняя релаксация) число итераций, необходимое для достижения сходимости возрастает[24], однако при этом снижается вероятность получения расходящегося решения. И наоборот, использование коэффициента релаксации r>1 (верхняя релаксация), может привести к сокращению продолжительности расчета, а может вызвать полный "развал" численной схемы.

Следует подчеркнуть, что выбор метода дискретизации дифференциальных уравнений и оптимальной величины коэффициента релаксации возлагается на исследователя[25]. Дополнительные сведения по этому вопросу содержатся в главе, посвященной свойствам разностных схем.

4.2 Метод конечных элементов

В основе метода конечных элементов (МКЭ) лежит предположение о характере поведения функции 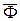, являющейся точным решением дифференциального уравнения. Для демонстрации основных идей МКЭ, предположим, что с достаточной точностью искомое решение 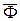(x) может быть представлено с помощью кусочно-линейной интерполяции[26] (рис. 9).

Очевидно, что значение кусочно-линейной функции Ф_*=Ф(х_*) в некоторой точке х_*, лежащей внутри отрезка [x_i-1, x_i] может быть найдено по формуле:

Рис. 9. Кусочно-линейная интерполяция решения дифференциального уравнения

,

(27)

где

.

(27а)

График функции формы (пробной функции) , приведен на рис. 10. Необходимо отметить, что функция формы, является локальной, т.е. она отлична от нуля лишь в некоторой области, непосредственно прилегающей к рассматриваемому узлу x_i. В частности, в случае кусочно-линейной интерполяции функции одной переменной 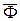(x), функция формы отлична от нуля лишь в пределах отрезков (конечных элементов) [x_i-1, x_i] и [x_i, x_i+1].

Рис. 10. Линейная функция формы

Отметим также, что производная кусочно-линейной функции Ф(х) в пределах элемента [x_i-1, x_i] совпадает с конечно-разностным отношением назад (9а), а в пределах элемента [x_i, x_i+1] – с конечно-разностным отношением вперед (9b).

Продемонстрируем применение метода конечных элементов на примере рассмотренного нами ранее обыкновенного дифференциального уравнения (13). Для сокращения записи будем использовать обозначение F(x)= .

Подстановка в уравнение (13) вместо точного решения 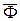(x) кусочно-линейной функции Ф(х) приведет к тому, что уравнение (13) будет выполняться неточно. Можно записать:

, хÎ[х0; хN].

(28)

Или:

, хÎ[ х0; хN],

(28а)

где R(х) – невязка решения, в общем случае являющаяся функцией независимой переменной х. Очевидно, что кусочно-линейная функция Ф(х) будет хорошим приближением к точному решению 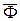(x) лишь в том случае, если невязка R(x) будет мала для всех значений хÎ[ х₀; х_N].

Второй принципиальный этап МКЭ заключается в выборе способа определения неизвестных узловых значений Ф_i. Для решения этой задачи потребуем, чтобы взвешенные интегралы невязки по всей области задания функции 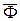(x) были равны нулю:

, для всех i=1…N

(29)

Вследствие локальности функций формы (см. рис. 10), можно записать:

для всех i=1…N

(30)

Или:

(30а)

Все интегралы, входящие в (30а), могут быть сравнительно легко определены, а сами соотношения (30а), совместно с начальным условием Ф₀= 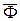(х₀), являются системой линейных алгебраических уравнений, которая может быть решена любым из известных методов, т.е.:

(30b)

Следует обратить внимание на то, что матрица системы линейных алгебраических уравнений (30b) имеет специфическую диагональную (ленточную) структуру. Для решения систем уравнений с ленточными матрицами, в вычислительной математике разработан ряд специальных методов, позволяющих существенно уменьшить объем вычислительной работы, самый распространенный из этих методов, называется методом прогонки.

Результаты решения дифференциального уравнения (13) методом конечных элементов приведены на рис. 11. Как можно видеть из этого рисунка, уже при шаге сетки Δх=0,08 численное решение, полученное с помощью МКЭ, гораздо лучше соответствует точному решению, чем численное решение, полученное с помощью метода Эйлера при шаге сетки Δх=0,025 (см. рис. 4). Следует, однако, отметить, что объем вычислительной работы, связанный с определением интегралов, входящих в (30), и последующее решение полученной системы алгебраических уравнений, на порядок превосходит объем вычислительной работы, выполненной по методу Эйлера.

Метод конечных элементов естественным образом распространяется на случай функций нескольких переменных. При этом, как правило, оказывается удобнее задавать каждую из функций формы в локальной системе координат, связанной с рассматриваемым узлом расчетной сетки. В качестве примера, на рис. 12 приведен график полилинейной функции формы , определенной на плоской сетке, содержащей треугольные конечные элементы.

Рис. 11. Решение дифференциального уравнения (13) методом конечных элементов

Рис. 12. Полилинейная функция формы , определенная на плоской сетке,

содержащей треугольные конечные элементы

4.3 Метод конечных объемов

Использование метода конечных (контрольных) объемов продемонстрируем на примере двумерного стационарного уравнения теплопроводности:

,

(31)

где α – коэффициент теплопроводности, S – скорость выделения теплоты в единице объема.

Решение задачи начнем с построения разностной сетки и разбиения расчетной области на непересекающиеся ячейки (объемы), каждая из которых содержит лишь один узел сетки (рис. 13). Проинтегрируем уравнение (31) по объему ячейки А:

(31а)

Рис. 13. Расчетная сетка, используемая для решения уравнения (31)

методом конечных объемов

Используя теорему о среднем можно записать

,

(32)

где Δх, Δу – длины граней ячейки, x_W – абсцисса левой ("западной") границы ячейки А, x_Е – абсцисса правой ("восточной") границы, у_N – ордината верхней ("северной") границы, у_S – ордината нижней ("южной") границы, S_* – средняя по ячейке скорость тепловыделения. Индекс у производных (_*), в левой части (32), указывает на то, что их следует рассматривать как средние значения, определенные таким образом, чтобы правильно представить тепловые потоки на каждой из границ. С учетом данного обстоятельства, дискретный аналог (32) может быть получен без затруднений [Патанкар].

Таким образом, уравнение (32) описывает баланс тепла (закон сохранения энергии) в пределах ячейки А. При условии правильного описания тепловых потоков между ячейками, система, составленная из уравнений вида (32), примененных к каждому контрольному объему, будет верно описывать баланс тепла во всей расчетной области.

В завершение параграфа следует отметить, что в частных случаях расчетные формулы, полученные описанными выше способами, могут совпадать, а наиболее существенные отличия проявляются при использовании криволинейных неортогональных расчетных сеток.