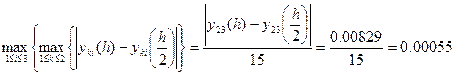Дифференциальных уравнений

I. Численное решение дифференциальных уравнений первого порядка.

1.Дифференциальное уравнение первого порядка, разрешенное относительно производной, имеет вид:

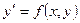(1)

Решением дифференциального уравнения (1) называется функция 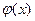, подстановка которой в уравнение обращает его в тождество: 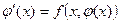. График решения 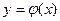называется интегральной кривой. Например, решением уравнения 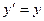является функция 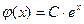при любом значении произвольной постоянной .

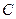Задача Коши для дифференциального уравнения (1) состоит в том, чтобы найти решение уравнения (1), удовлетворяющее начальному условию

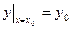(2)

Пару чисел 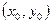называют начальными данными. Решение задачи Коши называется частным решением уравнения (1) при условии (2). Например, частным решением задачи Коши

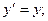
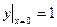
Является функция .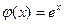

Частному решению соответствует одна из интегральных кривых, проходящая через точку .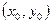

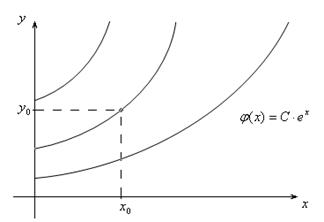Условие существования и единственности решения задачи Коши:

Теорема 1: Пусть функция 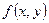- правая часть дифференциального уравнения (1) – непрерывна вместе со своей частной производной 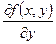по переменной 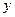в некоторой области 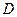на плоскости. Тогда при любых начальных данных 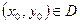задача Коши (1) – (2) имеет единственное решение .

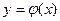При выполнении условий теоремы через точку 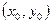на плоскости проходит единственная интегральная кривая. Будем считать, что условия теоремы выполняются!

Численное решение задачи Коши (1) – (2) состоит в том, чтобы получить искомое решение 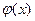в виде таблицы его приближенных значений для заданных значений аргумента 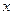на некотором отрезке :

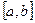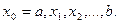(3)

Точки (3) называют узловыми точками, а множество этих точек называют сеткой на 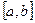. Будем использовать равномерную сетку с шагом :

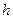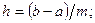
или ( )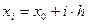

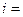
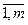Приближенные значения численного метода решения задачи Коши в узловых точках 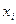обозначим через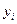

, ( ).

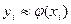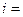
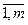Для любого численного метода решения задачи (1) – (2) начальное условие (2) выполняется точно, то есть .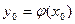

Величина погрешности численного метода решения задачи Коши на сетке отрезка 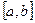оценивается величиной

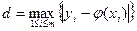
Говорят, что численный метод имеет 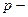ый порядок точности по шагу 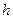на сетке, если расстояние 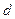можно представить в виде степенной функции от :

,

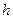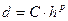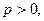
где С – некоторая положительная постоянная, зависящая от правой части уравнения (1) и от рассматриваемого метода.

|| Очевидно, что при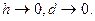

1. Метод Эйлера

Простейший численный метод решения задачи (1) – (2), иногда называемый методом ломанных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке 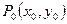есть

.

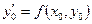Найдем ординату 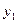касательной, соответствующей абсциссе 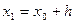. Так как уравнение касательной к кривой в точке 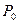имеет вид 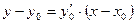, то

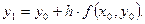
Угловой коэффициент в точке 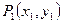также находится из данного дифференциального уравнения 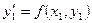. На следующем шаге получаем новую точку 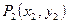, причем

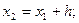
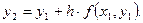
Продолжая вычисления в соответствии с намеченной схемой получим формулы Эйлера для 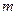приближенных значений решения задачи Коши с начальными данными 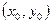на сетке отрезка 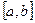с шагом :

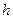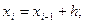
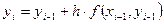
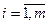(4)

Графическая иллюстрация приближенного решения.

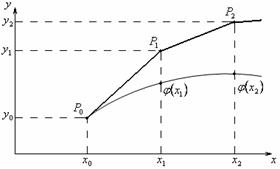ломаная Эйлера.

интегральная кривая – точное значение задачи Коши.

Оценим погрешность метода Эйлера на одном шаге. Для этого запишем разложение точного решения задачи Коши в точке 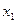по формуле Тейлора с остаточным членом в форме Лагранжа:

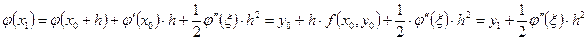
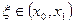
Погрешность метода на одном шаге имеет порядок 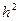, так как

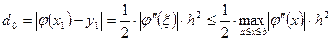
После 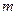шагов погрешность вычисления значения 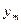в конечной точке отрезка возрастает не более чем в 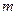раз.

Погрешность метода Эйлера можно оценить неравенством

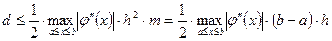
Или представить в ви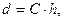де

где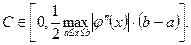

Это означает что метод Эйлера имеет первый порядок точности. В частности, при уменьшении шага 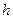в 10 раз погрешность уменьшается примерно в 10 раз.

Практическую оценку погрешности решения, найденного на сетке с шагом 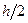, в точке 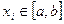производят с помощью приближенного равенства – правила Рунге:

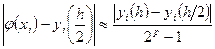, (5)

где p – порядок точности численного метода.

Таким образом, оценка полученного результата по формуле (5) вынуждает проводить вычисления дважды: один раз с шагом 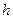, другой – с .

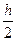Пример: Решить задачу Коши 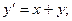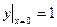методом Эйлера на отрезке .

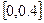Найти решение на равномерной сетке с шагом 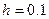в четырех узловых точках. Найти решение в тех же узлах, ведя расчет с шагом .

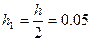Вычислить погрешности приближений с шагом :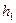

a) с помощью формулы (5);

b) сравнить с точным решением. Аналитическое решение задачи имеет вид:

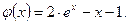
Решение: Здесь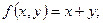

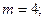
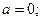
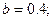
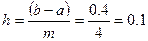
Используя рекуррентные формулы

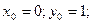
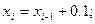
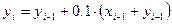
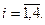
Последовательно находим

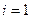
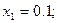
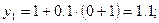
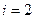
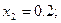
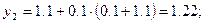
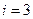
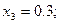
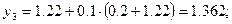
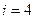
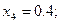
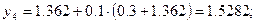
Аналогично находим решения для шага ;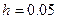

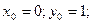
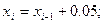
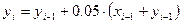
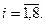
Обозначим 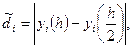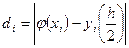и представим результаты вычислений в таблице (для узлов с шагом )

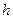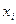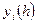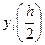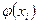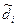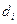0.1	1.1	1.105	1.110342	0.005	0.005342
0.2	1.22	1.231012	1.242805	0.011012	0.011793
0.3	1.362	1.380191	1.399718	0.018191	0.019527
0.4	1.5258	1.554911	1.583649	0.026711	0.028738

Оценки погрешностей 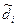решения 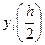, вычисляемых по формулам (5) 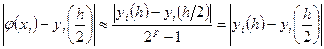(так как р=1 – метод Эйлера имеет первый порядок точности) близки к отклонениям 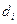. Обе величины достигают значения 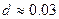, то есть имеют тот же порядок, что и шаг .

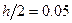Погрешность же при вычислениях с шагом 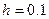составляет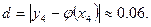

|| Таким образом, уменьшая шаг 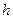вдвое, снижаем погрешность в два раза!

1. Методы Рунге – Кутта.

Численные методы решения задачи Коши

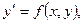
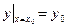
На равномерной сетке 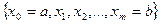отрезка 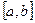с шагом 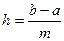являются методами Рунге – Кутта, если, начиная с данных 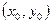, решение ведется по следующим рекуррентным формулам:

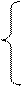
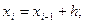
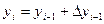
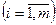
(6)

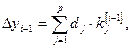
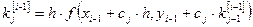
где 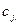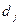- некоторые коэффициенты.

Метод называют методом Рунге – Кутта порядка 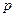, если он имеет 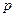-й порядок точности по шагу 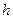на сетке.

Порядок точности 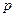достигается с помощью формул (6) при определенных значениях коэффициентов 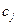и 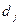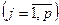. 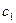всегда полагают равным нулю 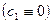. Коэффициенты 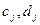вычисляются по следующей схеме:

1). Точное решение 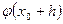и его приближение 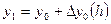представляют в виде разложения по формуле Тейлора с центром 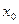вплоть до слагаемого порядка .

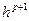2). Из равенств подобных членов при одинаковых степенях 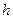в двух разложениях получают уравнения, решая которые, находят коэффициенты 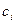и .

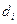Метод Эйлера можно назвать методом Рунге – Кутта первого порядка!

Действительно, для 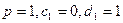формулы (6) преобразуются в соотношения метода Эйлера:

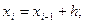
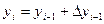
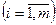
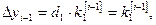
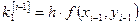
или

.

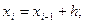
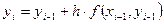3.1Метод Эйлера – Коши – метод Рунге – Кутта при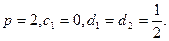

Из формулы (6) получаем:

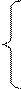
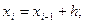
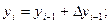
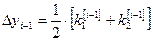
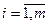
(7)

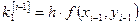
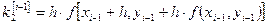
Для практической оценки погрешности решения можно применять правило Рунге (5), полагая 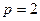, то есть:

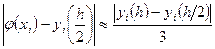
Пример: решить задачу Коши 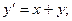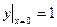методом Эйлера – Коши на отрезке 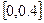. Найти решение на равномерной сетке с шагом 0.1 в четырех узловых точках.

Решение: Формулы (7) принимают вид:

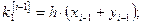
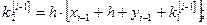
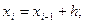
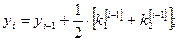
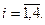
Полагая 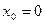, 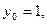последовательно находим

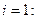
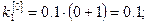
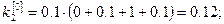
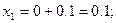
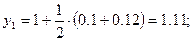
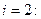
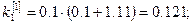
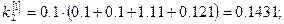
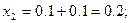
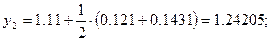
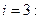
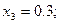
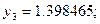
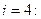
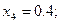
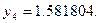
Погрешность полученного решения не превышает величины

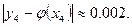
3.2Классический метод Рунге – Кутта

(метод Рунге – Кутта четвертого порядка)

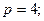
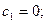
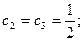
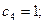
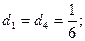
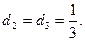
Из формул (6) при данных значениях 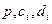получаем:

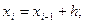
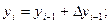
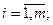
(8)

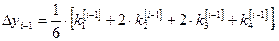
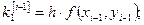
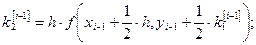
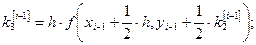
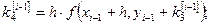
Графиком приближенного решения является ломаная, последовательно соединяющая точки 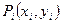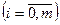. С увеличением порядка численного метода звенья ломанной приближаются к ломанной, образованной хордами интегральной кривой 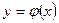, последовательно соединенными точками 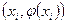на интегральной кривой.

Правило Рунге практической оценки погрешности решения для численного метода четвертого порядка имеет вид:

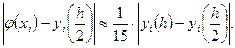
Пример: Решить задачу Коши 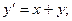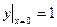классическим методом Рунге – Кутта на отрезке 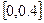. Найти решение на равномерной сетке с шагом 0.1 в четырех узловых точках.

Решение: Так как 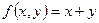, то по формулам (8) получаем:

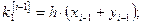
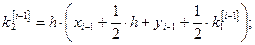
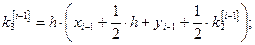
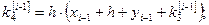
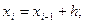
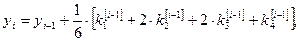
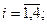
Полагая 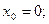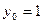, последовательно находим:

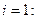
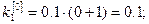
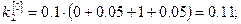
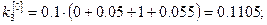
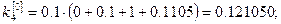
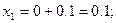
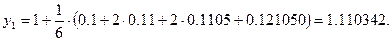
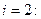
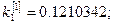
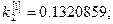
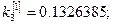
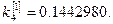
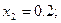
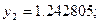
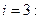
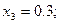
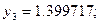
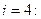
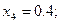
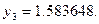
Погрешность полученного решения не превышает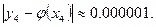

Результаты примеров 1-3 сведены в таблицу:

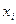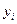	, найденные методом	Точное решение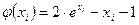
Эйлера	Эйлера – Коши	Рунге – Кутта
0.0	1.0	1.0	1.0	1.0
0.1	1.1	1.11	1.110342	1.110342
0.2	1.22	1.24205	1.242805	1.242805
0.3	1.362	1.398465	1.399717	1.399718
0.4	1.5282	1.581804	1.583648	1.583649

Блок-схема численного решения задачи Коши для дифференциального уравнения первого порядка методами Эблера, Эблера-Коши и Рунге-Кутта.

(решение задачи Коши).

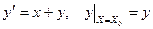
Численное решение систем дифференциальных

уравнений первого порядка

Пусть дана система 2-х ДУ 1-го порядка:

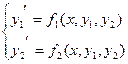(1)

Тогда функци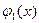и и 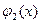называется решением системы (1), если

, .

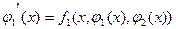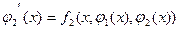Решению 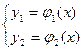системы (1) соответствует интегральная кривая в 3-х мерном пространстве .

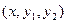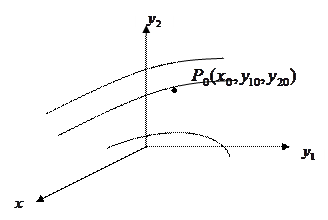
Условия, при которых через каждую точку 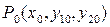некоторой области D 3-х мерного пространства проходит единственная кривая, содержатся в следующей теореме:

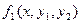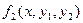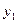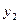Теорема. Если функции и - правые части ДУ системы (1) – непрерывны вместе со своими частными производными то переменным и в некоторой области D 3-хмерного пространства, те для любой точки 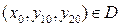система (1) имеет единственное решение, удовлетворяющее начальным условиям.

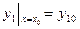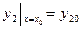, (2)

Задача Кошидля системы n дифференциальных уравнений1-го порядка: требуется найти решение системы:

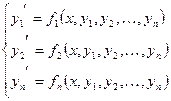(3)

При начальных условиях

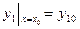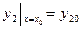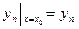; ; (4)

Теорема существования и единственности решения задачи Коши (3) – (n) аналогична теореме для случая n=2.

Введем векторные обозначения:

; ; ; .

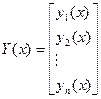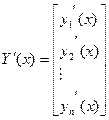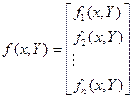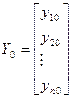Тогда задача Коши (3) – (n) запишется в виде:

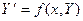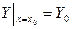; (5)

Численное решение задачи Коши (5) состоит в том, что на сетке отрезка 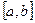требуется получить приближенные значения координат вектора 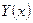в узлах сетки .

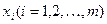Обозначим вектор, аппроксимирующий решение, через 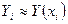, , 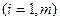а его координаты – через 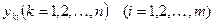так, что 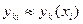или

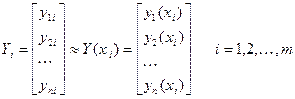
Будем искать решение на равномерной сетке с шагом .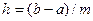

Величина погрешности численного метода оценивается величиной

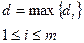, где 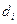- погрешность решения на сетке с шагом 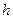в точке :

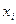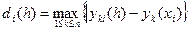
(т.е. в каждой точке I находится max погрешность по всем n координатам, а затем ищется max погрешность по все m точкам).

Практически погрешность решения в точке 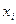оценивается по формуле Рунге:

Пусть ; .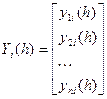

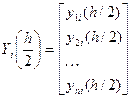Тогда погрешность 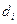в точке 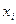, для вычислений с шагом 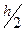выражается приближенным равенством.

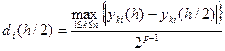(6)

Где Р – порядок численного метода.

Численное решение задачи Коши для системы DY находится с помощью классического метода Р-К – т.е. метода 4-го порядка.

Векторная форма алгоритма метода Р-К для задачи (5) аналогична рекуррентным формулам одномерной задачи.

(7)

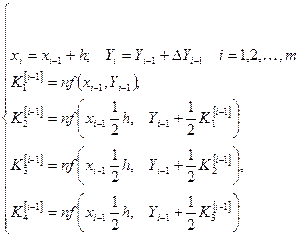
Где векторы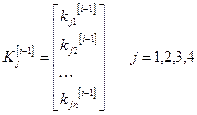

Пример. Найти численное решение задачи Коши для системы 2-х ДУ.

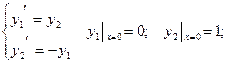
На сетке отрезка 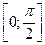методом Рунге-Кутта.

Вычисления провести с шагам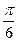и и .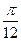

Оценить погрешность по принципу Рунге.

Аналитическое решение задачи .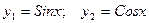

Решение:

Здесь

.

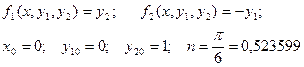Численное решение ищем по формулам (7).

Последовательно вычисляя, пр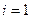и и 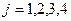имеем:

.

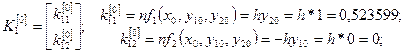
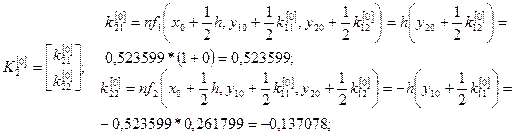
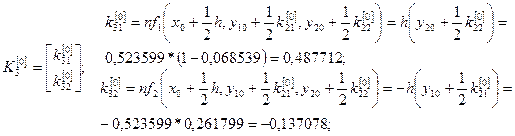
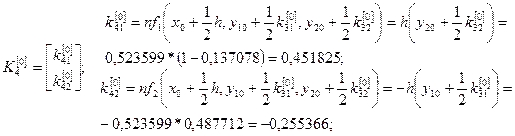
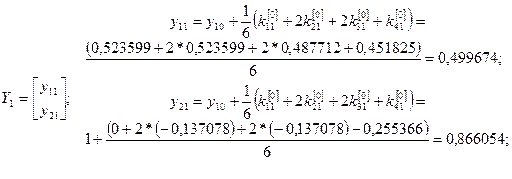
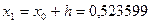Продолжая процесс вычислений, получим:

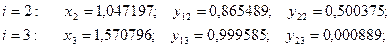
Результаты численного решения задачи с шагом 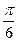и 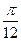сведены в таблицу.

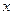	Численное решение задачи Коши	Точное решение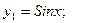
с шагом	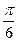с шагом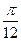
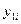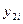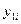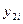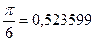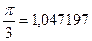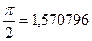	0,499674   0,865489   0,999585	0,866054   0,500375   0,000889	0,49980   0,865998   0,999987	0,866032   0,500030   0,000060	0,5   0,866253

Используя правило Рунге, находим погрешность.