Глава 14. теория функций комплексного переменного.

Расширенной (или полной) комплексной плоскостью называется комплексная плоскость переменной 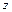с присоединением единственного комплексного числа 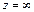(независимо от направления), окрестностью которой называется множество точек, удовлетворяющих условию .

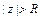Функция 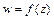однозначна, если каждому значению 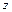из некоторой области ставится в соответствие одно, определённое комплексное число .

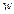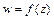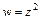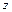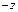Функция называется однолистной в некоторой области, если в различных точках этой области она принимает различные значения. Например, функция - однозначна, но не однолистна, так как двум точкам на комплексной плоскости и отвечает одно и тоже значение .

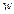Для расширенной комплексной плоскости множество точек, состоящее из внутренних точек, любые две из которых можно соединить непрерывной кривой, все точки которой принадлежат этому множеству, называется связной областью.

Функция 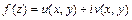называется дифференцируемой в точке 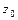, если существует 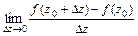, независимый от способа стремления 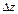к нулю. Этот предел называется производной функции .

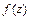Если функция 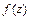дифференцируема в точке 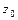, то существуют частные производные 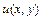, 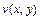и выполняются соотношения, называемые условиями Коши-Римана: , .

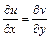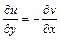Функция 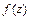, имеющая в каждой точке некоторой области непрерывную производную, называется аналитической в этой области. Например, функция 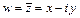- непрерывна на всей плоскости, но нигде не дифференцируема, т.е. не аналитическая.

Функция 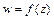, где 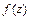- однозначная аналитическая в некоторой области 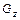, осуществляет отображение этой области на область 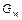комплексной плоскости 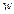, называемое конформным. Например, показательная функция 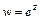отображает полосу на плоскости 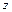шириной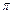 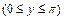на верхнюю полуплоскость 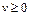, а функция отображает полуполосу 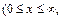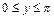) на полукруг единичного радиуса в верхней полуплоскости .

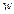Конформное отображение в точке 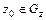во-первых, сохраняет углы между любыми гладкими линиями, проходящими через точку 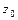и угол поворота бесконечно малого элемента равен аргументу производной 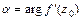и, во-вторых растяжение бесконечно малого элемента в точке 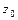постоянно и равно модулю производной 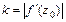для любого направления.

Функция 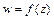, осуществляющая конформное отображение заданной односвязной области 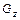на область 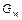в плоскости 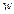, определяется единственным образом заданием соответствия между тремя различными точкам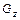и и .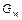

Интеграл от комплексной функции 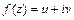по некоторой кусочно-гладкой линии 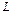конечной длины, определяется следующей формулой

,

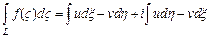где 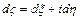, и интегралы в правой части равенства – криволинейные интегралы второго рода. В частности, если 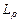- окружность радиуса 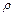с центром в точке 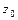, обходимая в положительном направлении (против хода часовой стрелки) ( 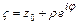), то 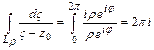и не зависит ни от 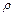, ни от .

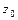В интегральном исчислении теории функций комплексного переменного основную роль играет теорема Коши: Если 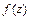- аналитическая функция в некоторой односвязной области 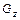, то интеграл 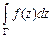, взятый вдоль любого замкнутого контура 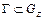, равен нулю.

Значения аналитической функции в точке, лежащей внутри замкнутого контура 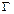определяется интегралом Коши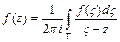 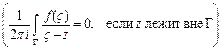, а её 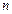-ая производная во внутренних точках области 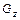равна .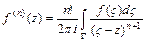

Если функции 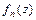( 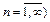аналитические в некоторой области 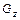и ряд 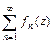равномерно сходится в каждой точке замкнутой области 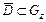, то 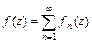- аналитическая в 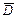и .

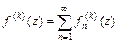Функция 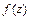- аналитическая внутри круга 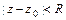может быть представлена в этом круге единственным образом 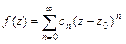, где 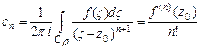, 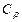- окружность радиуса 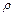с центром в точке .

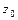Ряд вида 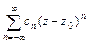, сходящийся в кольце 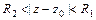к аналитической функции 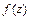, называется рядом Лорана этой функции. Здесь 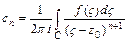( 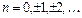), 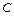- произвольный замкнутый контур в кольце 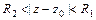, содержащий точку 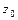внутри.

Точка 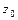называется правильной, если существует ряд Тейлора 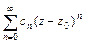сходящийся к 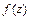внутри круга сходимости, принадлежащему 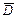. Точки 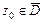не являющиеся правильными называются особыми точками .

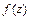Точка 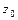называется:

1)устранимой особой точкой функции 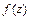, если ( );

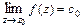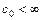2)полюсом порядка 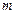функции 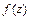, если её ряд Лорана в окрестности 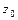содержит 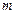членов с отрицательными степенями ;

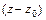3)существенно особой точкой функции 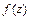, если её ряд Лорана в окрестности 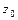содержит бесконечное число членов с отрицательными степенями .

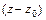Вычетом аналитической функции 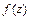в изолированной особой точке 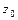называется число равное интегралу 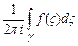, где 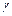- замкнутый контур, содержащий изолированную особую точку, взятый в положительном направлении, и обозначается в виде : .

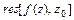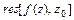
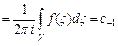Для полюса 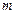-го порядка имеем

.

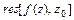
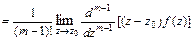В частности, для полюса первого порядка .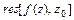

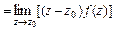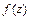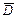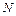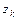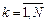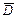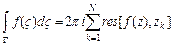Если функция аналитическая всюду в замкнутой области , за исключением конечного числа изолированных особых точек ( ), лежащих внутри области , то , где 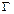полная граница области 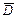, проходимая в положительном направлении. Ели функция 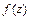аналитическая в расширенной плоскости, за исключением конечного числа 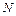изолированных особых точек 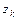( 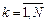), включая 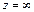, то .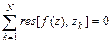

Теорию вычетов широко применяют для вычисления интегралов.