Линейные дифференциальные уравнения
Пример 11. Найти общее решение (общий интеграл) уравнения
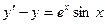 .
.
Решение уравнения ищем в виде 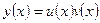 (или, в краткой форме,
(или, в краткой форме,  ). Продифференцируем это равенство по
). Продифференцируем это равенство по  :
:  . Подставив теперь выражения для
. Подставив теперь выражения для  и
и  в данное уравнение, получим
в данное уравнение, получим
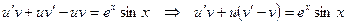 . (21)
. (21)
Выберем функцию 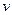 так, чтобы
так, чтобы 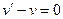 , т.е. в качестве
, т.е. в качестве 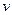 выберем любое (ненулевое!) частное решение уравнения
выберем любое (ненулевое!) частное решение уравнения 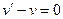 . Тогда
. Тогда
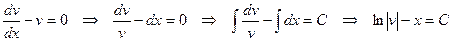 .
.
Положим 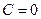 (поскольку нам нужно одно решение); отсюда
(поскольку нам нужно одно решение); отсюда
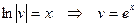 .
.
Подставим 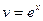 в уравнение (21), которое принимает вид
в уравнение (21), которое принимает вид
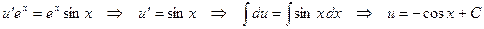 .
.
Итак, общее решение исходного уравнения
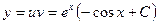 .
.
Пример 12. Найти решение задачи Коши 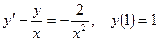 .
.
Производя подстановку  ,
,  , получим
, получим
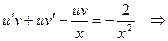
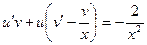 . (22)
. (22)
Выберем (ненулевую) функцию 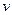 так, чтобы
так, чтобы
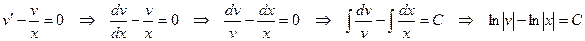 ,
,
и, полагая 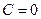 , получим
, получим 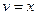 .
.
Подставим 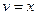 в уравнение (22):
в уравнение (22):
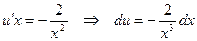
Интегрируя последнее уравнение, находим 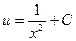 , откуда получаем общее решение исходного уравнения
, откуда получаем общее решение исходного уравнения
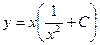 .
.
Воспользуемся начальным условием 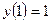 и найдем
и найдем 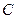 :
:
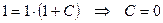 .
.
Итак, решение задачи Коши имеет вид 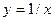 .
.
Дифференциальные уравнения высших порядков
Пример 13. Найти общее решение ДУ 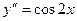 .
.
Интегрирование по  обеих частей уравнения понижает порядок уравнения на единицу. Получаем
обеих частей уравнения понижает порядок уравнения на единицу. Получаем 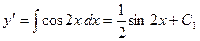 .
.
Проинтегрировав полученное уравнение, находим 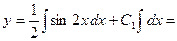
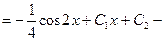 общее решение уравнения.
общее решение уравнения.
Пример 14. Найти частное решение ДУ 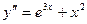 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 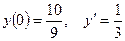 .
.
Общее решение ДУ найдем последовательным интегрированием уравнения
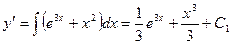 , (23)
, (23)
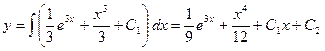 . (24)
. (24)
Воспользуемся начальными условиями, подставив 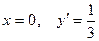 в (23),
в (23), 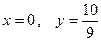 в (24).
в (24).
Получим
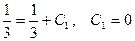 ,
,
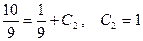 .
.
Таким образом, 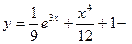 частное решение ДУ, удовлетворяющее начальным условиям.
частное решение ДУ, удовлетворяющее начальным условиям.
Пример 15. Найти общее решение ДУ 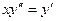 .
.
Это уравнение не содержит явно искомой функции  , что позволяет понизить его порядок. Обозначим
, что позволяет понизить его порядок. Обозначим 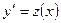 , тогда
, тогда 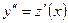 . Уравнение принимает вид
. Уравнение принимает вид 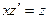 . Это ДУ с разделяющимися переменными.
. Это ДУ с разделяющимися переменными. 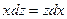 .
.
После разделения переменных получим 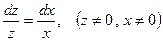
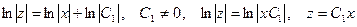 или
или 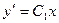 .
.
Интегрируем по  :
: 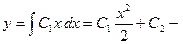 общее решение данного ДУ.
общее решение данного ДУ.
Пример 16. Найти общее решение ДУ 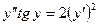 .
.
Это ДУ, не содержащее явно независимой переменной  . Подстановка
. Подстановка  понижает порядок уравнения на единицу. Имеем
понижает порядок уравнения на единицу. Имеем 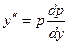 . Тогда
. Тогда 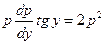 . Получили уравнение с разделяющимися переменными. После разделения переменных имеем
. Получили уравнение с разделяющимися переменными. После разделения переменных имеем 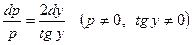 .
.
Интегрируем 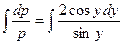 или
или 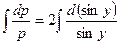 ,
,
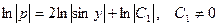 или
или 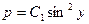 . Заменяем
. Заменяем 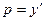 .
.
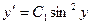 или
или 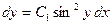 . Это ДУ с разделяющимися переменными. Разделяя переменные, получим
. Это ДУ с разделяющимися переменными. Разделяя переменные, получим 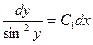 . Интегрируем
. Интегрируем 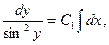
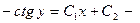 общий интеграл ДУ. Решением является
общий интеграл ДУ. Решением является 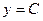 , кроме
, кроме 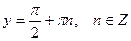 .
.
Пример 17. Найти решение задачи Коши 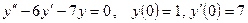 .
.
Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Составляем характеристическое уравнение, заменяя 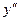 на
на 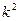 ,
,  на
на  , а
, а  на 1. Получаем
на 1. Получаем 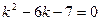 . Корни уравнения
. Корни уравнения 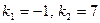 вещественные и различные. Этим корням соответствуют частные линейно независимые решения
вещественные и различные. Этим корням соответствуют частные линейно независимые решения 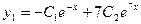 . Используя начальные условия
. Используя начальные условия 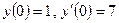 , получим систему уравнений
, получим систему уравнений
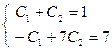
Решая ее, находим 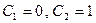 .
.
Таким образом, 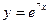 - решение задачи Коши.
- решение задачи Коши.
Пример 18. Найти общее решение ДУ 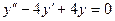 .
.
Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Составим характеристическое уравнение, заменяя 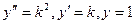 .
.
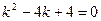 . Корни уравнения
. Корни уравнения 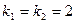 вещественные и равные. Этим корням соответствуют частные линейно независимые решения
вещественные и равные. Этим корням соответствуют частные линейно независимые решения 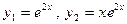 . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид 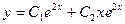 .
.
Пример 19. Найти общее решение уравнения 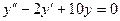 .
.
Соответствующее характеристическое уравнение имеет вид 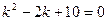 . Корни уравнения
. Корни уравнения 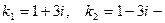 комплексные. Этим корням соответствуют частные линейно независимые решения
комплексные. Этим корням соответствуют частные линейно независимые решения 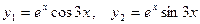 . Общее решение имеет вид
. Общее решение имеет вид 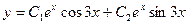 .
.
Пример 20. Найти общее решение ДУ 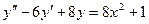 .
.
Это линейное неоднородное ДУ второго порядка с постоянными коэффициентами. Его общее решение 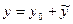 , где
, где 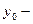 общее решение соответствующего однородного уравнения,
общее решение соответствующего однородного уравнения, 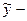 частное решение неоднородного уравнения. Решим однородное уравнение
частное решение неоднородного уравнения. Решим однородное уравнение 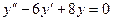 . Соответствующее характеристическое уравнение имеет вид
. Соответствующее характеристическое уравнение имеет вид 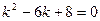 . Корни уравнения
. Корни уравнения 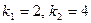 - вещественные и различные. Общее решение имеет вид
- вещественные и различные. Общее решение имеет вид 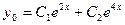 . Так как ни один из корней характеристического уравнения не равен нулю, то частное решение ищем в виде
. Так как ни один из корней характеристического уравнения не равен нулю, то частное решение ищем в виде 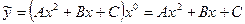 . Найдем
. Найдем 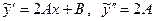 . Подставим
. Подставим 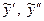 в исходное уравнение. Получим
в исходное уравнение. Получим
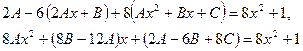
Приравнивая коэффициенты при одинаковых степенях  в обеих частях равенства, получаем систему уравнений:
в обеих частях равенства, получаем систему уравнений:
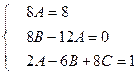
Решая ее, находим 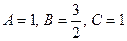 .
.
Итак, частное решение данного ДУ имеет вид 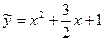 , а его общее решение
, а его общее решение 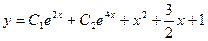 .
.
Задачи для самостоятельного решения
Найти общее решение или общий интеграл дифференциальных уравнений.
1. 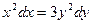 11.
11. 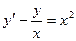
2. 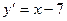 12.
12. 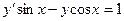
3. 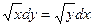 13.
13. 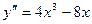
4. 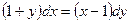 14.
14. 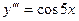
5. 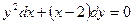 15.
15. 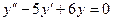
6. 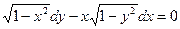 16.
16. 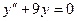
7. 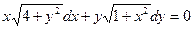 17.
17. 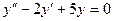
8. 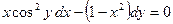 18.
18. 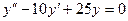
9. 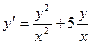 19.
19. 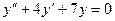
10. 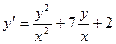 20.
20. 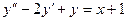
Найти решение задачи Коши.
1. 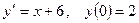
2. 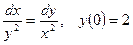
3. 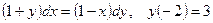
4. 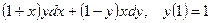
5. 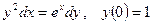
6. 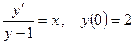
7. 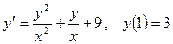
8. 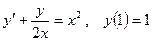
9. 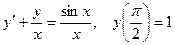
10. 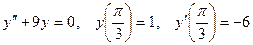
11. 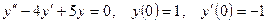 .
.
