Канал с аддитивным гауссовским шумом

Сигнал на выходе такого канала

Z(t) = γu(t-τ) + N(t) = s(t) + N(t), (4.48)

где N(t) — гауссовский аддитивный шум с нулевым математическим ожидани­ем и заданной корреляционной функцией. Чаще всего рассматривается белый гауссовский шум (БГШ) либо квазибелый (с равномерной спектральной плот­ностью в полосе спектра сигнала s(t)). Часто при анализе можно τ не учиты­вать, что соответствует изменению начала отсчёта времени на выходе канала. Некоторое усложнение модели (4.48) получается, если коэффициенты передачи γ и запаздывания τ считать известными функциями времени: Z(t) = y(t)u[t-j(t)] + N(t).

Такая модель удовлетворительно описывает многие проводные каналы, ра­диоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надёжно предсказать значения γ и τ.

9.Непрерывный канал. Канал с неопределённой фазой сигнала и аддитивным шумом. Однолучевой канал с замираниями.

Эта модель отличается от модели (4.48) тем, что в ней запаздывание явля­ется случайной величиной. Для узкополосных сигналов с учётом (4.44) выра­жение (4.48) при постоянном γ и случайных τ можно представить в виде ,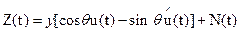

где 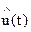-преобразование Гильберта от u(t); θ = -w₀τ-случайная фаза. Рас­пределение вероятностей θ предполагается заданным, чаще всего равномерным на интервале от 0 до 2π. Эта модель удовлетворительно описывает те же кана­лы, что и предыдущая, если фаза сигнала в них флуктуирует. Такая флуктуа­ция вызывается небольшими изменениями протяжённости канала, свойств среды, в которой проходит сигнал, а также фазовой нестабильностью опорных генераторов.

Однолучевой гауссовский канал с общими замираниями (флуктуациями амплитуд и фаз сигнала) также описывается формулой (4.48), но множительγ,как и фаза θ, считаются случайными процессами. Иными словами, случайны­ми будут квадратурные компоненты X = γcosθ, Y=γsinθ.

При изменении квадратурных компонент X, Y во времени принимаемое ко­лебание 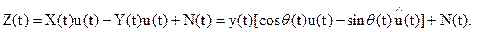(4.49) Как отмечалось выше, одномерное распределение коэффициента передачи канала γ может быть рэлеевским или обобщённым рэлеевским. Такие каналы называют соответственно каналами с рэлеевскими или обобщёнными рэлеевскими (или райсовскими) замираниями. В рамках общей гауссовской модели канала [14] γ имеет четырёхпараметрическое распределение. Модель однолучевого канала с замираниями достаточно хорошо описывает многие каналы ра­диосвязи в различных диапазонах волн, а также некоторые другие каналы.

Многолучевой гауссовский канал с селективными по частоте замираниями обобщает модель (4.49):

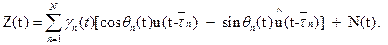, (4.50)

где N — число лучей в канале; 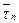- среднее время задержки для n-го луча. Многолучевая общая гауссовская модель хорошо описывает многие каналы ра­диосвязи. Для модели (4.50) условия (4.46) не выполняется, если под ∆τ пони­мать запаздывания между лучами.