Примерные темы курсовых работ. Вопросы для подготовки к теоретической части э
- Симметрические многочлены.
- Линейные неравенства.
- Строение конечных абелевых групп.
- Строение конечных полей.
- Группы самосовмещений фигур и тел.
- Группы подстановок.
- Алгебры с делением над полем
 .
. - Частично упорядоченные множества.
- История развития теории решения уравнений в радикалах.
- Элементы теории полей.
- Циклические группы. Кольца на циклических группах.
- Отделение действительных корней многочленов с действительными коэффициентами.
- Тело кватернионов.
- Арифметика кольца целых гауссовых чисел.
Вопросы для подготовки к теоретической части экзамена.
Семестр
- Операция сложения комплексных чисел, записанных в алгебраической форме. Свойства сложения.
- Операция умножения комплексных чисел, записанных в алгебраической форме. Свойства умножения.
- Тригонометрическая форма комплексного числа. Умножение комплексных чисел, записанных в тригонометрической форме.
- Формула Муавра. Деление комплексных чисел, записанных в тригонометрической форме.
- Извлечение корня n-й степени из комплексного числа.
- Извлечение корня n-й степени из единицы.
- Перестановки. Инверсии. Транспозиции. Теорема о транспозиции в перестановке.
- Определение детерминанта (определителя) порядка n. Свойства 1-5.
- Определение детерминанта (определителя) порядка n. Свойства 6-10.
- Вычисление определителей 2-ого и 3-его порядков. Способы вычисления определителей порядка n.
- Миноры. Алгебраические дополнения. Теорема о разложении определителя по строке.
- Миноры. Алгебраические дополнения. Теорема о сумме произведений элементов некоторой строки определителя на алгебраические дополнения к элементам этой строки.
- Равносильные системы. Элементарные преобразования систем линейных уравнений.
- Метод Гаусса.
- Теорема Крамера.
Семестр
1. Операции сложения матриц и умножения матрицы на число. Свойства этих операций.
2. Операция умножения матриц. Свойства умножения.
3. Обратная матрица. Критерий существования обратной матрицы.
4. Определение векторного пространства. Примеры, свойства.
5. Определение линейной зависимости и линейной независимости системы векторов. Свойства.
6. Основная теорема о линейной зависимости.
7. Максимальная линейно независимая подсистема системы векторов. Свойства.
8. Базис векторного пространства. Свойства.
9. координаты вектора в базисе. Координаты суммы векторов и произведения вектора на число.
10. Отношение «линейно выражаться» на множестве всех подсистем векторного пространства. Свойства этого отношения.
11. Элементарные преобразования систем векторов. Эквивалентные системы векторов.
12. Линейная оболочка системы векторов. Теорема о линейной оболочке.
13. Критерий равенства линейных оболочек подсистем A и B.
14. Строчный, столбцовый ранги матрицы. Доказать, что строчный ранг матрицы не изменится, если переставить местами 2 строки или 2 столбца данной матрицы.
15. Строчный, столбцовый, минорный ранги матрицы. Теорема о ранге матрицы.
16. Теорема Кронекера-Капелли.
17. Подпространство решений однородной системы. Теорема о связи множества решений неоднородной системы и множества решений соответствующей однородной системы.
18. Теорема о числе решений фундаментальной системы.
19. Алгебраические операции, примеры. Свойства бинарных операций.
20. Определение группы, примеры. Единственность нейтрального и обратного элемента в группе.
21. Определение группы. Примеры. Свойства групп.
22. Подгруппы. Признаки подгруппы.
23. Определение кольца. Свойства колец. подкольца. Признаки подкольца.
24. Определение поля. Свойства полей. Подполе. Признак подполя.
Семестр
1. Построение кольца многочленов от одной переменной.
2. Отношение делимости в кольце многочленов. Свойства.
3. Теорема о существовании частного и остатка.
4. Теорема единственности частного и остатка.
5. НОД многочленов. Алгоритм Евклида.
6. Свойства НОДа.
7. Линейная форма НОД двух многочленов.
8. Взаимно простые многочлены. Свойства.
9. Производная многочлена. Свойства производной.
10. Кратность корня. Связь кратности корня с производной данного многочлена.
11. Теорема Безу. Схема Горнера.
12. Основная теорема алгебры многочленов. Следствия из неё.
13. Формулы Виета.
14. Решение уравнений 3-ей степени.
15. Решение уравнений 4-ей степени.
16. Приводимые и неприводимые многочлены. Свойства.
17. теорема о разложении многочлена на неприводимые множители.
18. Неприводимость и приводимость многочленов над полями 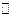 и
и 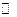 .
.
19. Критерий приводимости многочленов 2-й и 3-ей степени над полем 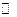 .
.
20. примитивный многочлен. Представление всякого многочлена из Q[x] в виде произведения примитивного многочлена на некоторое рациональное число.
21. Лемма Гаусса.
22. Критерий Эйзенштейна.
Семестр
1. Определение векторного пространства, примеры, свойства.
2. Подпространства. Примеры. Критерий подпространства.
3. Линейно зависимые и линейно независимые системы векторов. Свойства.
4. Пересечение и сумма подпространств.
5. Прямая сумма подпространств. Критерий прямой суммы.
6. Теорема о размерности суммы подпространств.
7. Нахождение базиса суммы и базиса пересечения подпространств.
8. Изоморфизм векторных пространств. Теорема об изоморфизме конечномерных векторных пространств.
9. Критерий линейной независимости образов системы векторов при изоморфизме векторных пространств.
10. Умножения числовой матрицы на векторную матрицу-столбец. Свойства этого умножения.
11. Матрица перехода от одного базиса к другому. Невырожденность матрицы перехода.
12. Связь между матрицей перехода от базиса е к базису е' и матрицей перехода от базиса е' к базису е. Связь между координатами одного и того же вектора в разных базисах.
13. Определение линейного оператора. Свойства линейного оператора. Матрица линейного оператора.
14. Образ и ядро линейного оператора.
15. Теорема о сумме ранга и дефекта.
16. Теорема о существовании и единственности линейного оператора, переводящего линейно независимую систему из k векторов в произвольную систему из k векторов.
17. Подобные матрицы. Подобие матриц одного и того же линейного оператора в разных базисах.
18. Характеристическая матрица. Характеристические корни матрицы. Равенство характеристических многочленов подобных матриц.
19. Собственные векторы и собственные значения линейного оператора. Теорема о связи между собственными значениями линейного оператора и характеристическими корнями матрицы этого линейного оператора.
20. Критерий диагональности матрицы линейного оператора.
21. Линейная независимость собственных векторов линейного оператора, относящихся к различным собственным значениям.
22. Группы. Свойства групп. Подгруппы.
23. Действия над степенями элемента в группе.
24. Бесконечная циклическая группа. Теорема об изоморфизме бесконечной циклической группы и аддитивной группы целых чисел.
25. Конечные циклические группы.
26. Смежные классы по подгруппе. Свойства.
27. Теорема Лагранжа.
28. Определение нормального делителя. Критерий нормального делителя.
29. Фактор группа по нормальному делителю.
30. Гомоморфный образ группы. Первая теорема о гомоморфизмах групп.
31. Вторая теорема о гомоморфизмах групп.
