Математическая статистика

Закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее , чем больше объем статистического материала .

Результаты опытов, представленные в виде таблицы, в которой указываются значения измеряемой величины и их частота (статистический ряд или статистическая совокупность) могут быть использованы для построения эмпирической функции распределения.

Процесс нахождения эмпирической функции распределения 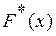аналогичен процессу нахождения функции распределения F =(x) дискретной случайной величины Х. Пусть выборка (статистический ряд) имеет вид

			…
			…

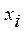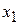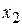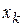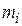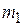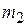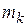где 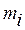- частота появления i-го значения и .

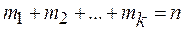Тогда функция распределения определяется следующим образом:

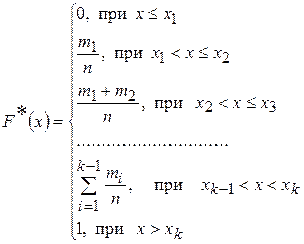
График эмпирической функции распределения строят также, как и график функции распределения F=(x) дискретной случайной величины.

Для нахождения закона распределения нужно располагать достаточно обширным статистическим материалом (порядка нескольких сотен опытов), а на практике приходится довольствоваться меньшим числом наблюдений, из которых нельзя найти неизвестный закон распределения случайной величины. Однако можно ориентировочно определить важнейшие числовые характеристики случайной величины.

На практике часто бывает, что вид распределения известен заранее, а требуется найти только параметры, от которых он зависит.

Любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, является случайным и называется оценкой параметра. Например, оценкой для математического ожидания может служить среднее арифметическое наблюдаемых значений случайной величины в n независимых опытах. Если число опытов невелико, то замена математического ожидания средним арифметическим приводит к некоторой ошибке, которая будет тем больше, чем меньше число опытов. То же относится и к другим числовым характеристикам. Оценка неизвестного параметра одним числом называется «точечной».

Точечные оценки указывают точку на числовой оси, в которой находится значение неизвестного параметра. Для определения оценок математического ожидания 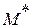и дисперсии 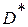случайной величины, значения которой

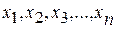
получены в результате n независимых измерений, следует пользоваться следующими приближенными формулами:

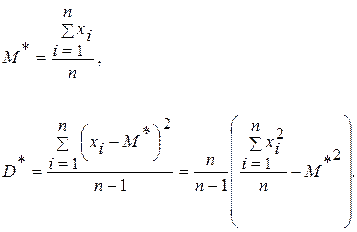
В ряде задач требуется не только найти для параметра распределения случайной величины его подходящее численное значение, но и оценить его надежность. Это особенно важно при малом числе наблюдений, так как точечная оценка в значительной мере случайна и это может привести к серьезным ошибкам.

Для определения точности оценки параметра в математической статистике пользуются доверительными интервалами, а для определения надежности – доверительными вероятностями. Задавая некоторую вероятность 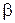, находят такое значение 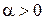, для которого выполняется равенство

,

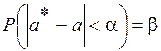где а - параметр, для которого из опыта получена несмещенная оценка 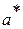. Раскрывая модуль, можно переписать это равенство в виде

.

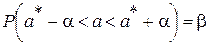Hеизвестное значение параметра а с вероятностью 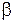попадает в интервал

,

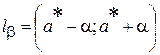который называется доверительным интервалом.

Задачу интервального оценивания можно сформулировать следующим образом: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри этого интервала находится оцениваемый параметр.

Точность оценки 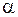фактически определяет длину доверительного интервала 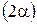. Любую точность можно получить с определенной вероятностью (надежностью). Доверительная вероятность 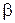задается обычно значением близким к единице, например 0,95; 0,98; 0,99 и т.п.

Доверительная вероятность 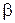, точность оценки 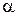и объем выборки n связаны между собой. Если определены две величины, то тем самым будет определена и третья.

6.1. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных ста книг. Найти относительную частоту появления бракованных книг.

Решение. По определению относительной частоты

,

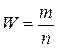где m = 5, n = 100. Отсюда W = 0,05.

6.2. Монету подбрасывают 1000 раз. Оценить снизу вероятность отклонения частоты W появления «герба» от вероятности р его появления меньше чем на 0,1.

Решение. Если вероятность события от испытания к испытанию не изменяется и равна p (схема Бернулли), то, как устанавливает теорема Бернулли, при неограниченном увеличении числа испытаний частота случайного события сходится по вероятности к вероятности события, т.е.

,

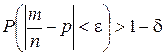причём можно принять, что

.

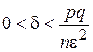Это один из законов больших чисел.

Здесь

N = 1000, р = q = 0,5, ε = 0,1.

По закону больших чисел

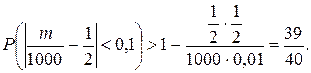
Неравенство

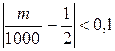
равносильно двойному неравенству 400 < m < 600, поэтому можно сказать, что вероятность попадания появлений «герба» в интервал (400; 600) больше чем .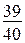

6.3. В урне сто белых и сто чёрных шаров. Вынули с возвращением 50 шаров. Оценить снизу вероятность того, что количество белых шаров из числа вынутых удовлетворяет двойному неравенству:

15 < m < 35.

Решение. Данное двойное неравенство можно переписать в виде

–10 < m –25 < 10,

или

.

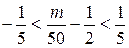Здесь n = 50, p = 0,5; по закону больших чисел (теорема Бернулли) оценим вероятность неравенства

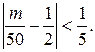
При

,

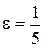получим

,

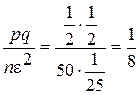поэтому

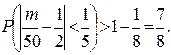6.4. Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в виде статистического ряда:

i

xi

i

xi

На основании опытных данных найти оценку неизвестных параметров M(X) и D(X) случайной величины X – напряжения тока.

Решение. Для того, чтобы полученная на основании опытных данных оценка а^* параметра а случайной величины X имела практическую ценность, она должна обладать следующими свойствами.

Во-первых, она должна быть несмещённой, т.е. M(а^*) = а, для того, чтобы не делать систематической ошибки в сторону завышения или занижения.

Во-вторых, оценка а^* параметра а должна быть состоятельной, т.е.

,

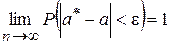где ε – сколь угодно малое.

В-третьих, оценка а^* должна быть эффективной, т.е. дисперсия оценки должна быть минимальной. Оценками математического ожидания M(X) и дисперсии D(X), обладающими такими свойствами, являются

.

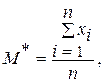
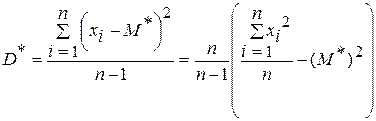Результаты вычислений будут такими:

M ^*= 220,25; D^* = 7,06.