Переходная и весовая функции объекта по каналу управления

Переходная функция h(t) определяется как переходной процесс на выходе звена при подаче на вход единичного ступенчатого воздействия 1(t) при нулевых начальных условиях. В нашем случае это значит, что расход пара в сушильных цилиндрах увеличивается

∆х=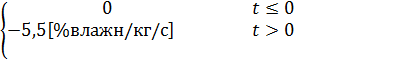

Переходная (временная)характеристика для звена первого порядка с запаздыванием определяется выражением :

h(t)= =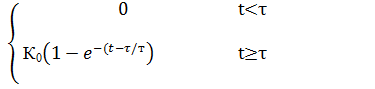

=

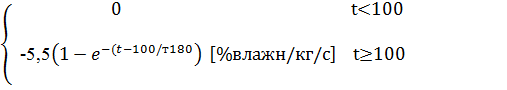
Для расчета переходной функции необходимо приблизительно оценить время окончания переходного процесса

Его можно вычислить по выражению:

t­_пер.пр. » (3 – 4)T+t

t­_пер.пр. » (3 – 4)180+100=840 c

Исходя из этого выберем шаг расчета:

Dt = ,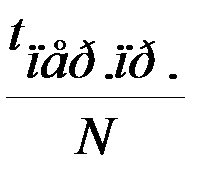

Где: N-желаемое количество точек графика;

N=14,

Dt = 840/14=60с

Весовая функция W(t) представляет собой переходной процесс на выходе звена на единичную импульсную функцию d [t] при нулевых начальных условиях. Единичная импульсная функция является производной от единичной ступенчатой функции d [t] =1¢ [t]. Переходная весовая функции связаны соотношением:

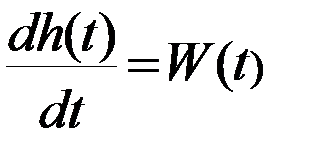
Весовая функция W(t) определяется по дифференциальному выражен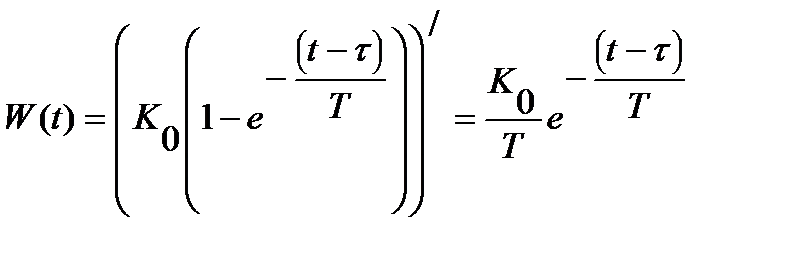 т.е.

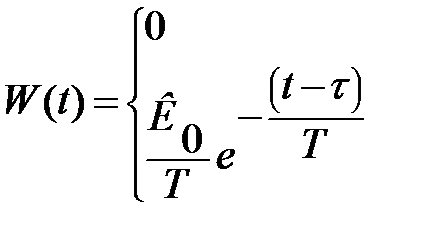при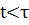

при ;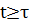

W(t)= ;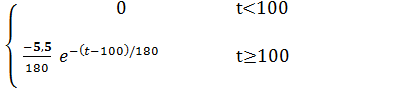

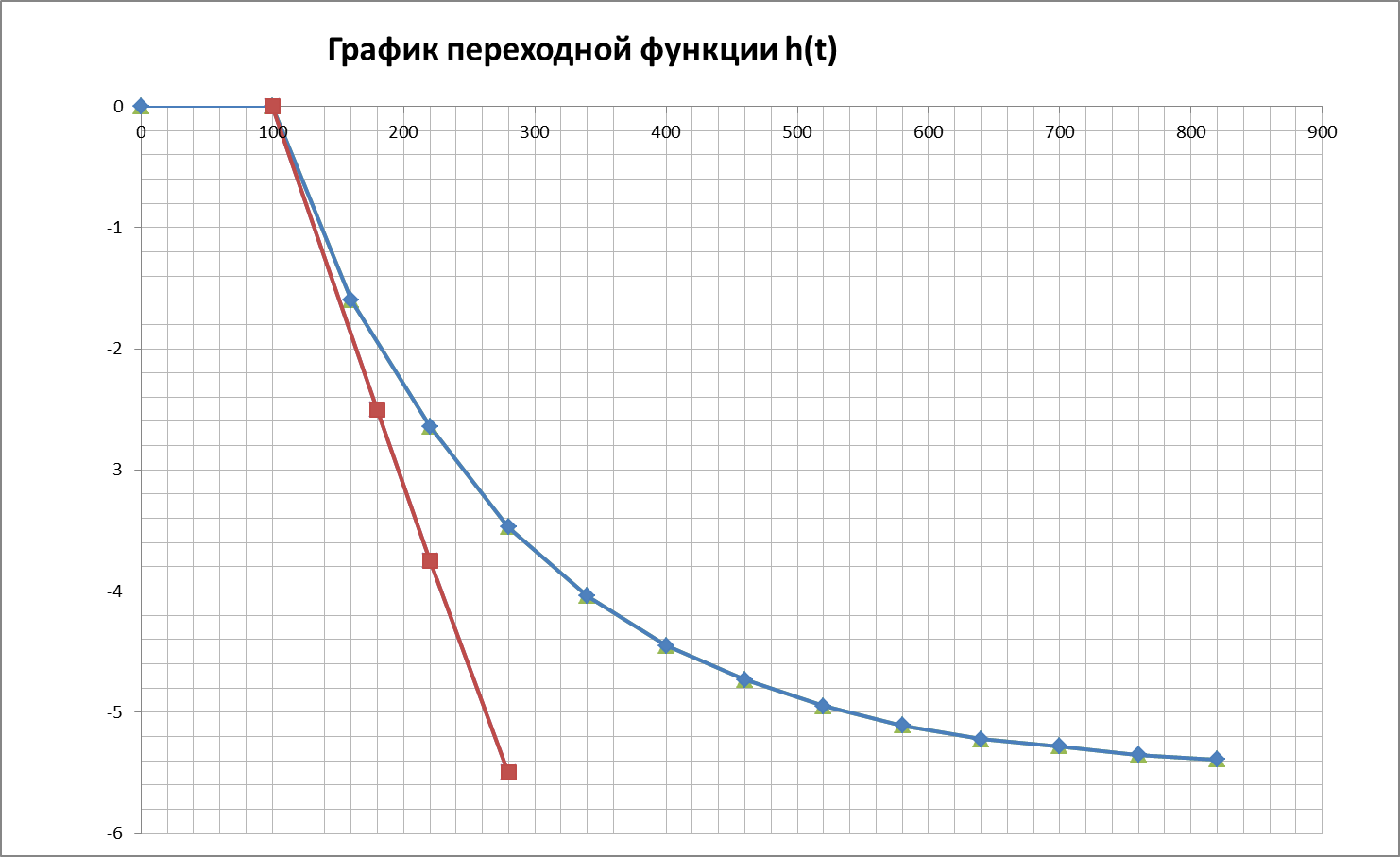
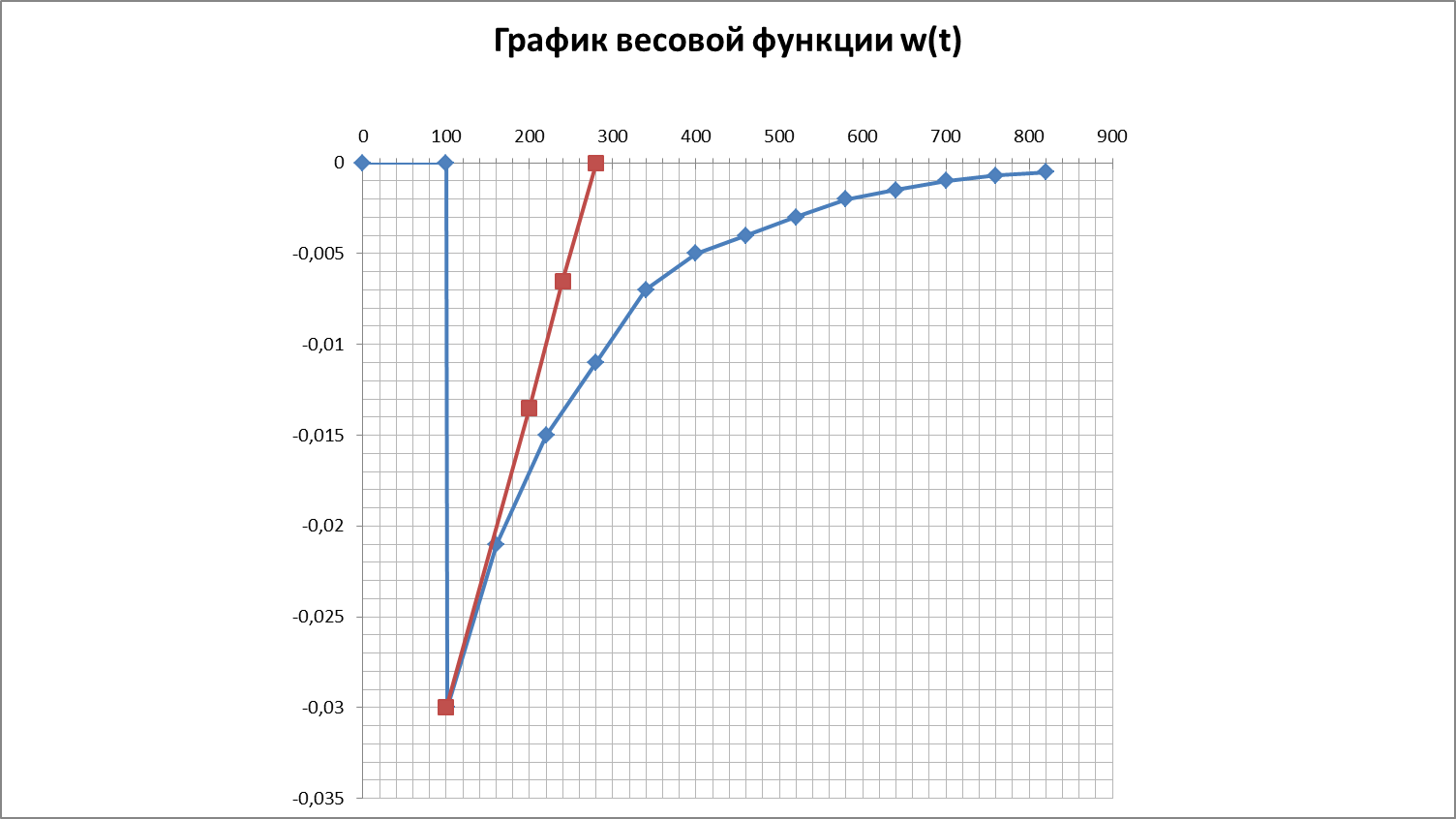
Результаты расчетов сведены в таблицу 1.и построены графики переходной и весовой функции объекта.

Таблица 1.

Расчет переходной и весовой функции объекта по каналу управления.

T c
h(t)			-1,6	-2,64	-3,47	-4,04	-4,45	-4,73	-4,95
W(t)		-0,03	-0,021	-0,015	-0,011	-0,007	-0,005	-0,004	-0,003
T c
h(t)	-5,11	-5,22	-5,28	-5,35	-5,39
W(t)	-0,002	-0,0015	-0,001	-0,0007	-0,0005

По данным Таблицы 1 построены графики переходной и весовой функции.

Основные параметры объекта по каналу управления могут быть определены из этих графиков.

Частотные характеристики объекта по каналу управления.

Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на _входе.

Выражения частотных характеристик по каналу управления могут быть получены из выражения частотной передаточной функции.

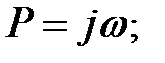
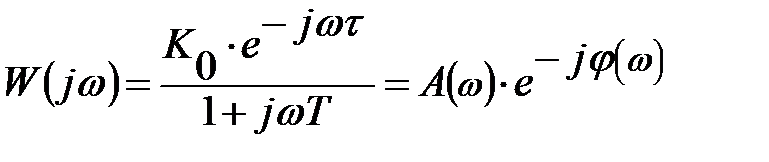
где А(w) - АЧХ объекта

j(w) - ФЧХ объекта

Зависимость отношения амплитуд выходных и входных колебаний от их частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость разности фазы выходных и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ) системы.

Найдем модуль частотной передаточной функции (АЧХ):

А(ω)= |К₀ |/ 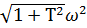=|-5,5|/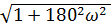

j(w)=-wτ-аrctgwT

Т.к. К₀ 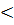0 ,то фыражение ФЧХ пишется в виде :

j(w)=-π-wτ-аrctgwT

Частота w_пр., определяющая полосу частот пропускания объекта, найдется из условия:

A(w_пр)= 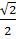А(w)_w=0

A(w_пр)= 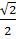К₀

w_пр = 1/Т = 1/180 = 0,005с ^-1

Частотные характеристики будем строить на диапазоне от 0 до 10-15 w_пр.

Результаты расчетов сведена в таблицу 2.

Таблица 2

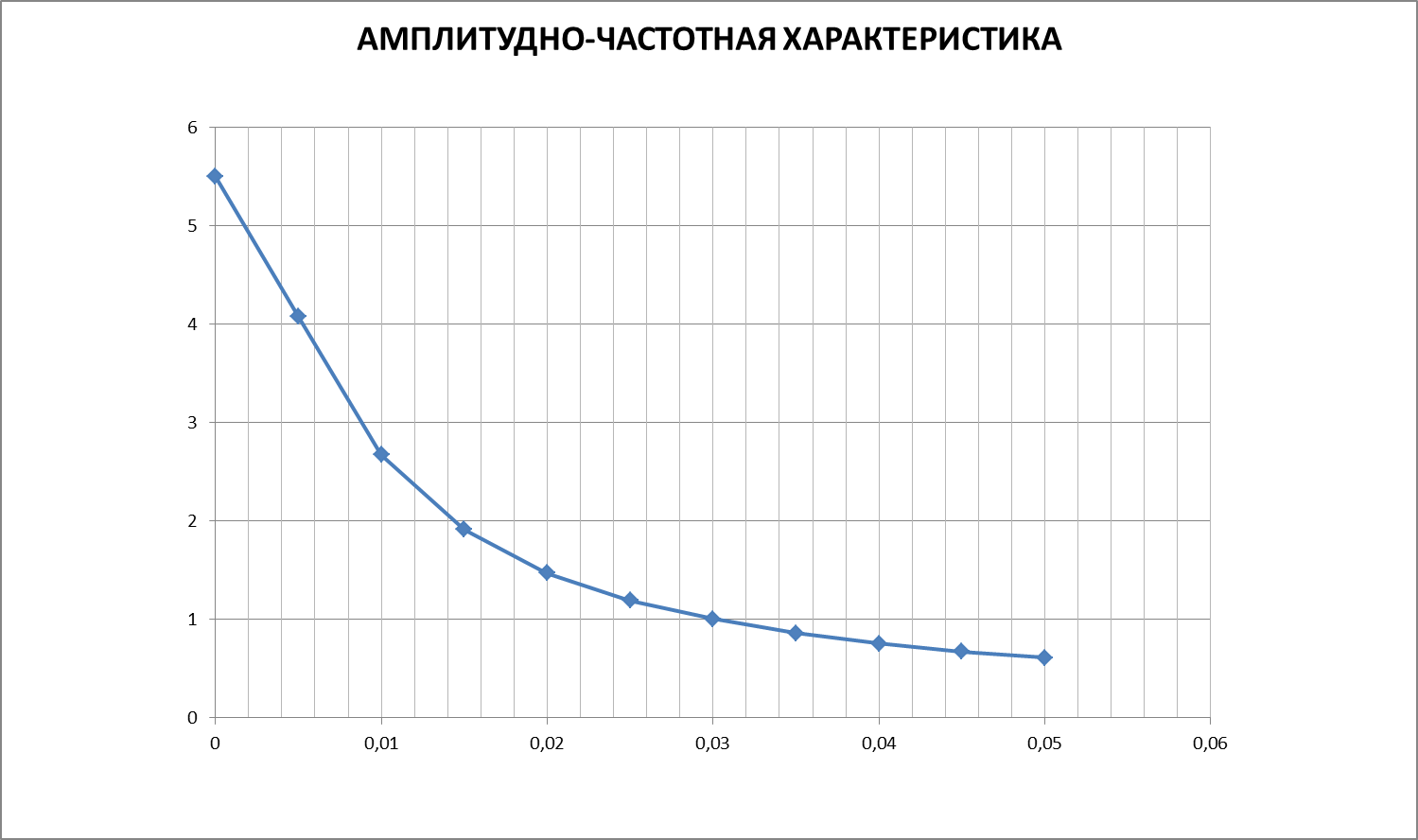
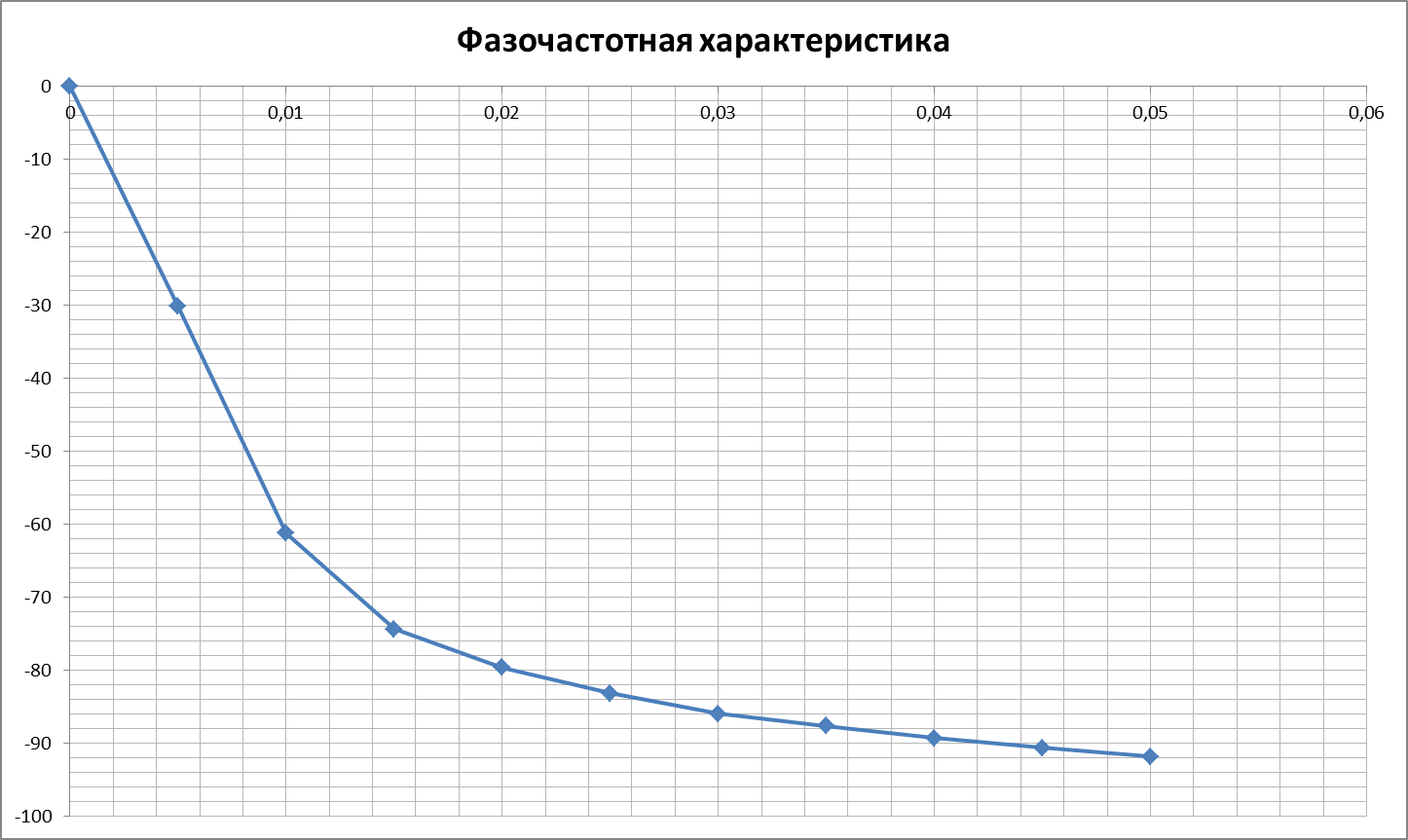
w, с-1		0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04	0,045	0,05
АЧХ,	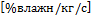5,5	4,08	2,67	1,91	1,47	1,19	1,001	0,86	0,75	0,67	0,607
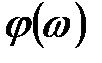, рад.		-30,14	-61,25	-74,31	-79,61	-83,11	-85,94	-87,62	-89,23	-90,6	-91,79

По данным таблицы 2 построены графики АЧХ и ФЧХ.

Из графика АЧХ видно,что чем меньше частота входного сигнала, тем больше этот сигнал усиливается.При ω=0 ,коэффициент усиления максимален и равен 5,5. При больших частотах выходная величина по модулю стремится к 0. Такие сигналы объект не пропустит.

5. Структурная схема системы регулирования

Структурная схема системы – графическое изображение АСР в виде совокупности динамических звеньев с указанием связей между ними.

Исходными данными для построения схемы служат передаточные функции звеньев.