Лекция 7. Производная функции. Правила дифференцирования
План лекции
7.1. Понятие производной, её механический и геометрический смысл.
7.2. Правила дифференцирования. Таблица основных производных.
7.3. Линейная функция и её свойства.
7.4. Прямая линия на плоскости.
7.5. Угол между двумя прямыми. Расстояние от точки до прямой.
7.6. Уравнения касательной и нормали к плоской кривой.
7.1
Задача 1. О скорости движущейся точки.Будем рассматривать прямолинейное движение некоторого твердого тела, которое будем считать материальной точкой. И пусть 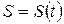 - закон движения тела, выражающий зависимость пройденного пути от времени, прошедшего с начала отсчета.
- закон движения тела, выражающий зависимость пройденного пути от времени, прошедшего с начала отсчета.
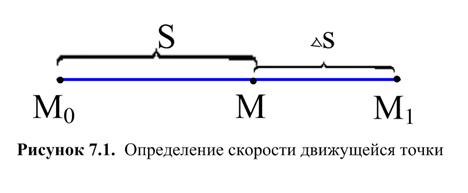
Пусть в некоторый элемент времени 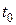 движущаяся точка
движущаяся точка 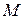 находилась на расстоянии
находилась на расстоянии 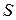 от начального положения
от начального положения 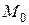 , а в некоторый следующий момент времени
, а в некоторый следующий момент времени 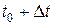 оказалась в положении
оказалась в положении 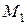 на расстоянии
на расстоянии 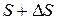 от начального положения. Таким образом, за промежуток времени
от начального положения. Таким образом, за промежуток времени 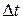 расстояние S изменилась на величину
расстояние S изменилась на величину 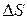 . В этом случае говорят, что за промежуток времени
. В этом случае говорят, что за промежуток времени 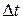 величина S получила приращение
величина S получила приращение 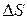 . Тогда средняя скорость движения за время
. Тогда средняя скорость движения за время 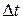 равна
равна
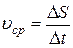 .
.
Средняя скорость не может точно охарактеризовать быстроту перемещения точки M в момент t. Однако, чем меньше 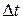 , тем лучше средняя скорость характеризует движение точки. Наиболее точно характеризует скорость движения тела в любой момент – мгновенная скорость:
, тем лучше средняя скорость характеризует движение точки. Наиболее точно характеризует скорость движения тела в любой момент – мгновенная скорость:
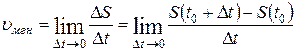 .
.
Задача 2. О нахождении наклона кривой в данной точке.Криволинейные связи, описываемые нелинейными функциями, отличаются от линейных постоянным изменением наклонам графиков нелинейных функций.
Возникает вопрос, как определить наклон в данной точке.
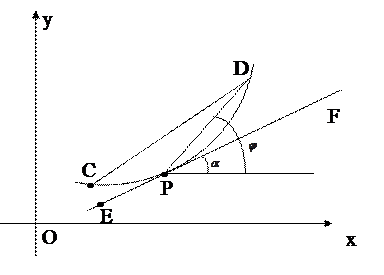 |
Рисунок 7.2.Нахождение наклона кривой в данной точке
Пусть задана некоторая кривая. Прямая CD - это хорда, соединяющая две точки на кривой.
С помощью очень коротких хорд подобных CD можно аппроксимировать кривую, и тогда наклон кривой в данной точке можно считать приблизительно равным наклону очень короткой хорды, проходящей через эту точку.
Пусть 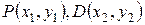 - две точки кривой, PD – хорда, EF – касательная к кривой в точке Р.
- две точки кривой, PD – хорда, EF – касательная к кривой в точке Р.
Наклон линии, соединяющей точки Р и D определяется по формуле
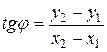 .
.
Предположив, что значения 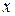 и
и 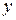 вдоль прямой между точками С и D меняются очень мало, обозначим
вдоль прямой между точками С и D меняются очень мало, обозначим 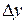 - очень малое приращение
- очень малое приращение 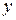 ,
, 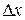 - очень малое приращение
- очень малое приращение 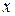 . Тогда
. Тогда
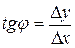 .
.
Это отношение в действительности определяет наклон хорды PD, однако по мере приближения точки D к P величина наклона хорды PD приближается к наклону касательной. Хорда PD будет поворачиваться вокруг P и угол 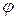 будет меняться с изменением
будет меняться с изменением 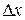 .
.
Если при 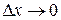 , угол
, угол 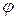 стремится к некоторому предельному положению угла
стремится к некоторому предельному положению угла 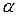 , то прямая, проходящая через точку Р и составляющая с положительным направлением ОХ угол
, то прямая, проходящая через точку Р и составляющая с положительным направлением ОХ угол 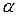 будет касательной, т.е. наклон графика в точке равен наклону касательной в этой точке. Можем записать
будет касательной, т.е. наклон графика в точке равен наклону касательной в этой точке. Можем записать
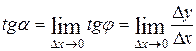 .
.
B задачах 1 и 2 мы получили пределы одного вида, что позволяет ввести определение новой операции.
Если существует предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, то этот предел называется производной функции 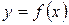 в данной точке
в данной точке 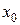 и обозначается
и обозначается
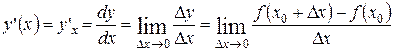 .
.
Задача 1 позволяет сформулировать механический смысл производной – скорость прямолинейного движения есть производная пути по времени: 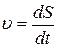 .
.
Задача 2 позволяет сформулировать геометрический смысл производной. Угловой коэффициент касательной к кривой 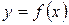 в данной точке равен значению производной в точке касания.
в данной точке равен значению производной в точке касания.
Операция нахождения производной называется дифференцированием. Функция, имеющая производную в точке  , называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке отрезка
, называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке отрезка 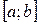 , называется дифференцируемой на этом отрезке.
, называется дифференцируемой на этом отрезке.
Рассмотрим порядок вычисления производной функции по определению:
1. Выбираем произвольную точку 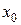 .
.
2. Придаем приращение аргументу 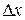 :
: 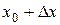 .
.
3. Определяем приращение функции 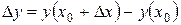 .
.
4. Находим отношение 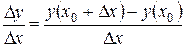 .
.
5. Вычисляем 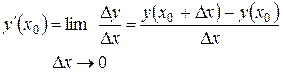 .
.
6. Так как точка 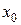 произвольная, то заменяя
произвольная, то заменяя 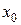 на
на 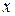 в формуле для
в формуле для 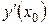 , получаем искомую производную функции в любой точке
, получаем искомую производную функции в любой точке 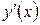 .
.
Пример 1. По определению найти производную функции 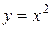 в произвольной точке х.
в произвольной точке х.
Решение. Выбираем произвольную точку 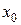 ; придаем приращение аргументу
; придаем приращение аргументу 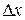 :
: 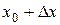 ;
;
вычисляем приращение функции 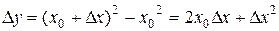 , тогда
, тогда
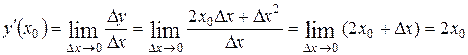 .
.
Следовательно, 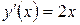 .
.
Пример 2. Найти скорость равномерно ускоренного движения в произвольный момент времени t и в момент t = 2 сек., если зависимость пути от времени 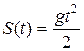 .
.
Решение. Выбираем произвольную точку 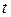 ; придаем приращение
; придаем приращение 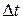 аргументу:
аргументу: 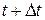 . Вычисляем приращение функции:
. Вычисляем приращение функции:
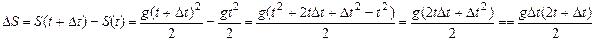 . Тогда скорость в произвольный момент времени будет равна
. Тогда скорость в произвольный момент времени будет равна
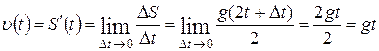 .
.
Скорость в момент времени t = 2 сек. соответственно будет
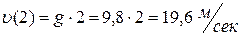 .
.
7.2
Вспомнимосновные правила дифференцирования:
1. Если 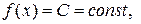 то
то 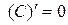 .
.
2. Если 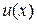 и
и 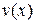 – дифференцируемые функции, то
– дифференцируемые функции, то
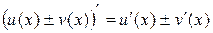 .
.
3. Если 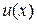 и
и 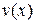 – дифференцируемые функции, то
– дифференцируемые функции, то
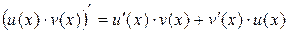 .
.
Следствие. Если 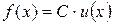 , то
, то 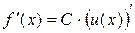 .
.
4. Если 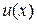 и
и 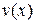 – дифференцируемые функции и
– дифференцируемые функции и 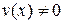 , то
, то
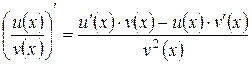 .
.
Следствие. Если 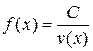 , то
, то 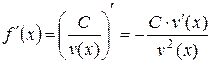 .
.
5. Если 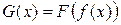 , то
, то 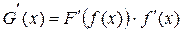 .
.
6. Если 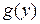 – есть функция обратная к
– есть функция обратная к 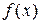 , то
, то 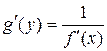 , где
, где 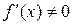 и
и  .
.
Для удобства нахождения производных составим таблицу основных производных.
Пусть 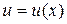 - дифференцируемая функция, тогда
- дифференцируемая функция, тогда
1. 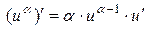 ;
;
2. 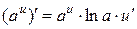 ;
;
3. 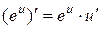 ;
;
4. 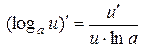 ;
;
5. 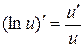 ;
;
6. 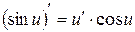 ;
;
7. 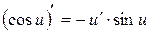 ;
;
8. 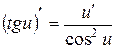 ;
;
9. 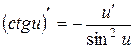
10. 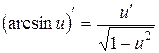 ;
;
11. 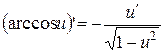 ;
;
12. 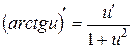 ;
;
13. 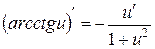 .
.
Производная 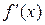 функции
функции 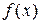 представляет собой некоторую функцию. Возможно, что эта новая функция сама имеет производную. Тогда производная функции
представляет собой некоторую функцию. Возможно, что эта новая функция сама имеет производную. Тогда производная функции 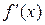 называется второй производной или производной 2-го порядка:
называется второй производной или производной 2-го порядка: 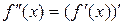 .
.
И вообще, производная от производной (n-1)-го порядка называется производной n-го порядка: 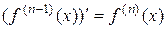 .
.
Пример 3. С помощью правил дифференцирования найдите производную функции 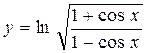 .
.
Решение. Для удобства дифференцирования преобразуем функцию 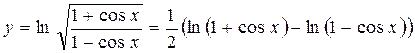 .
.
Тогда 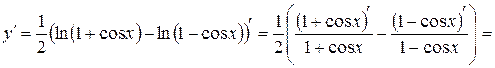
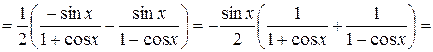
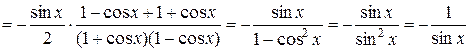 .
.
7.3
Функция вида 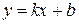 , где
, где 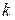 и
и 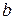 некоторые действительные числа носит название линейной функции. Рассмотрим основные свойства этой функции.
некоторые действительные числа носит название линейной функции. Рассмотрим основные свойства этой функции.
1. Очевидно, что функция определена для любого действительного значения аргумента, т.е. 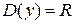 .
.
2. При 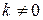 область значений
область значений 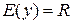 , а при
, а при 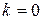
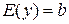 .
.
3. Функция пересекает ось 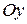 в точке
в точке 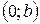 .
.
4. При 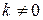 график функции пересекает ось
график функции пересекает ось 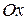 в точке
в точке 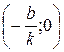 ; если
; если 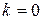 и
и 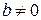 , то график функции ось
, то график функции ось 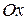 не пересекает; если
не пересекает; если 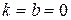 , то график функции совпадает с осью абсцисс.
, то график функции совпадает с осью абсцисс.
5. Если 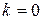 , то функция сохраняет знак
, то функция сохраняет знак 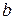 . Если
. Если 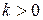 , то функция положительна при
, то функция положительна при 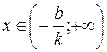 и отрицательна при
и отрицательна при 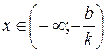 . Если
. Если 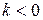 , то функция положительна при
, то функция положительна при 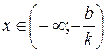 и отрицательна при
и отрицательна при 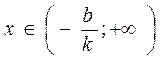 .
.
6. Выведем производную функции 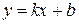 .
.
· Выбираем произвольную точку 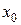 .
.
· Придаем приращение аргументу 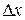 :
: 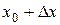 .
.
· Вычисляем приращение функции
· 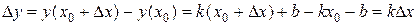 .
.
· Тогда 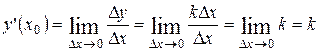 .
.
· Следовательно, 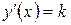 .
.
Таким образом, производная любой линейной функции равна угловому коэффициенту 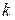 .
.
7. Если 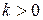 , то функция возрастающая. Если
, то функция возрастающая. Если 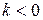 , то функция убывающая. При
, то функция убывающая. При 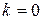 функция постоянная.
функция постоянная.
8. Графиком линейной функции является прямая (этот факт покажем в следующем пункте).
7.4
Линией на плоскости будем называть множество точек плоскости. Задать линию – значит указать, из каких точек плоскости она состоит. Это можно сделать при помощи уравнения с двумя неизвестными. Выберем на плоскости прямоугольную систему координат.
Уравнением линии на плоскости в прямоугольной системе координат называется уравнение вида 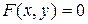 , которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты точек, которые не лежат на этой линии.
, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты точек, которые не лежат на этой линии.
Или можно сказать, что уравнение 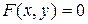 является уравнением некоторой линии при выполнении условий:
является уравнением некоторой линии при выполнении условий:
1. Если точка 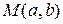 принадлежит линии, то координаты
принадлежит линии, то координаты 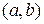 являются решением уравнения
являются решением уравнения 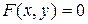 , то есть
, то есть 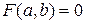 - верное числовое равенство.
- верное числовое равенство.
2. Если пара чисел 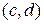 является решением уравнения, то точка
является решением уравнения, то точка 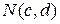 принадлежит данной линии.
принадлежит данной линии.
Простейшей линией на плоскости является прямая. Существуют различные способы задания прямой, это приводит к различным по форме уравнениям.
Пусть прямая 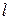 не параллельна оси
не параллельна оси 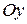 . Обозначим точку пересечения
. Обозначим точку пересечения 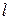 с осью
с осью 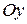
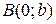 , угол между положительным направлением оси
, угол между положительным направлением оси 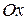 и прямой
и прямой 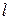 обозначим через
обозначим через 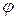 (Рисунок 7.3).
(Рисунок 7.3).
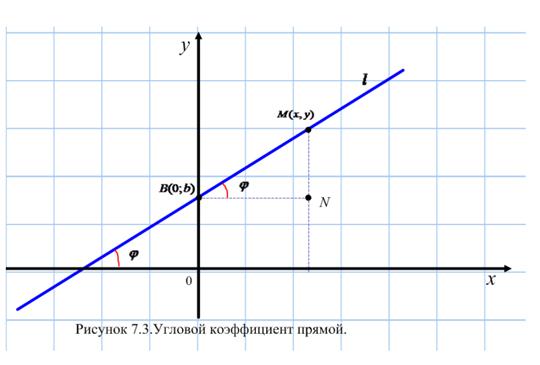
Пусть  - произвольная точка прямой
- произвольная точка прямой  . Из прямоугольного
. Из прямоугольного  :
:
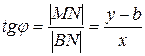 .
.
Обозначим через 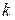 :
: 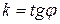 и назовем эту величину угловым коэффициентом прямой. Тогда
и назовем эту величину угловым коэффициентом прямой. Тогда 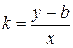 ,
,
откуда
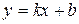 .(7.1)
.(7.1)
Уравнение (7.1) называется уравнением прямой с угловым коэффициентом.
Замечание. Прямая, параллельная оси  , не может быть задана уравнением с угловым коэффициентом.
, не может быть задана уравнением с угловым коэффициентом.
Рассмотрим другие способы задания прямой линии на плоскости.
Прямая может быть задана вектором нормали 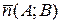 (вектором, перпендикулярным прямой) и точкой
(вектором, перпендикулярным прямой) и точкой 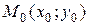 , лежащей на прямой. Пусть
, лежащей на прямой. Пусть 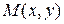 - произвольная точка прямой. Тогда векторы
- произвольная точка прямой. Тогда векторы 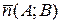 и
и 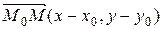 перпендикулярны, следовательно
перпендикулярны, следовательно 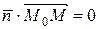 , или
, или 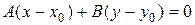 . Раскроем скобки и обозначим
. Раскроем скобки и обозначим 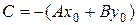 .
.
Уравнение вида
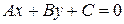 , (7.2)
, (7.2)
где 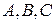 - заданные числа, причем
- заданные числа, причем 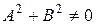 , называется общим уравнением прямой. Из предыдущего следует геометрический смысл коэффициентов общего уравнения прямой.
, называется общим уравнением прямой. Из предыдущего следует геометрический смысл коэффициентов общего уравнения прямой.
Если 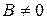 , то уравнение (7.2) можно записать в виде
, то уравнение (7.2) можно записать в виде 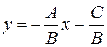 , или, полагая
, или, полагая 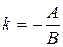 ,
, 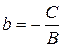 , получаем уравнение (7.1), то есть уравнение прямой, не параллельной оси
, получаем уравнение (7.1), то есть уравнение прямой, не параллельной оси 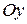 . Если
. Если 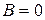 , то уравнение (7.2) принимает вид
, то уравнение (7.2) принимает вид 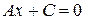 , где
, где 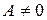 , или
, или 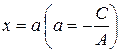 . Это уравнение на плоскости тоже задает прямую, но только параллельную оси
. Это уравнение на плоскости тоже задает прямую, но только параллельную оси 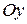 . Таким образом, доказана теорема.
. Таким образом, доказана теорема.
Теорема. Каждое уравнение первой степени на плоскости задает прямую, и, наоборот, каждая прямая на плоскости с прямоугольной системой координат определяется уравнением первой степени.
Заметим, что если в уравнении (7.2)
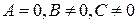 , то прямая параллельна оси
, то прямая параллельна оси 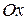 ;
;
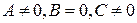 , то прямая параллельна оси
, то прямая параллельна оси 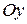 ;
;
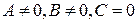 , то прямая проходит через
, то прямая проходит через 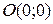 ;
;
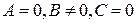 , то прямая совпадает с осью
, то прямая совпадает с осью 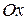 ;
;
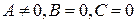 , то прямая совпадает с осью
, то прямая совпадает с осью 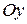 .
.
Пусть в уравнении (7.2) 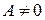 ,
, 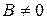 и
и 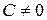 . Преобразуем его:
. Преобразуем его: 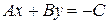 , разделим на
, разделим на 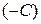 :
:  . Обозначим
. Обозначим 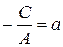 ,
, 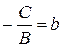 , получим
, получим
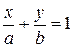 . (7.3)
. (7.3)
Уравнение (7.3) носит названиеуравнения прямой в отрезках, которое определяется тем, что 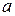 и
и 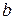 есть отрезки, отсекаемые прямой на осях координат (Рисунок 7.4).
есть отрезки, отсекаемые прямой на осях координат (Рисунок 7.4).
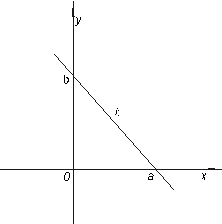
Рисунок 7.4. Уравнение прямой в отрезках.
Замечание. Прямые, параллельные координатным осям, и прямые, проходящие через начало координат, не могут быть записаны уравнением прямой в отрезках.
Если обе части общего уравнения прямой (7.2) умножить на число 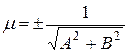 , которое называется нормирующим множителем, причем знак перед радикалом выбрать так, чтобы
, которое называется нормирующим множителем, причем знак перед радикалом выбрать так, чтобы 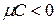 (при
(при 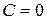 знак берем любой), то получится уравнение
знак берем любой), то получится уравнение
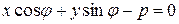 , (7.4)
, (7.4)
где 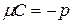 ,
, 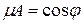 ,
, 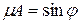 .
.

Рисунок 7.5. Нормальное уравнение прямой.
Уравнение вида (7.4) носит название нормального уравнения прямой. С геометрической точки зрения 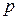 - длина перпендикуляра
- длина перпендикуляра 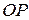 , опущенного из начала координат на прямую,
, опущенного из начала координат на прямую, 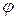 - угол, образованный этим перпендикуляром с положительным направлением оси
- угол, образованный этим перпендикуляром с положительным направлением оси 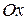 (Рисунок 7.5).
(Рисунок 7.5).
Для построения прямой на плоскости достаточно двух точек – через две различные точки на плоскости можно провести прямую и только одну. Выведем уравнение прямой, проходящей через две различные точки 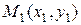 и
и 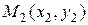 .
.
Пусть 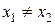 , тогда искомая прямая не параллельна оси
, тогда искомая прямая не параллельна оси 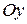 , поэтому её угловой коэффициент может быть найден по формуле
, поэтому её угловой коэффициент может быть найден по формуле 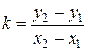 . С другой стороны, если взять
. С другой стороны, если взять 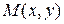 - произвольную точку на прямой, то угловой коэффициент можно выразить по формуле
- произвольную точку на прямой, то угловой коэффициент можно выразить по формуле 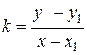 . Следовательно, можем получить уравнение
. Следовательно, можем получить уравнение 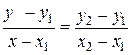 , или
, или
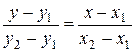 . (7.5)
. (7.5)
Замечание. Если 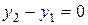 , то формально получили бы равенство
, то формально получили бы равенство 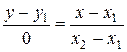 . Несмотря на его бессмысленность, такая запись удобна. Если освободиться от знаменателей, то получим верное равенство:
. Несмотря на его бессмысленность, такая запись удобна. Если освободиться от знаменателей, то получим верное равенство: 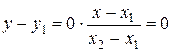 , или
, или 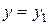 . Аналогично случай
. Аналогично случай 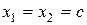 приводит к уравнению
приводит к уравнению 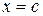 .
.
Прямая на плоскости может быть также задана направляющим вектором 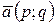 и точкой
и точкой 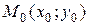 , лежащей на этой прямой. Пусть
, лежащей на этой прямой. Пусть 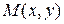 - произвольная точка прямой. Тогда векторы
- произвольная точка прямой. Тогда векторы 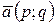 и
и 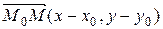 - коллинеарны, следовательно
- коллинеарны, следовательно 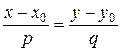 - уравнение искомой прямой. Последнее уравнение может быть переписано в виде
- уравнение искомой прямой. Последнее уравнение может быть переписано в виде 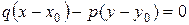 или
или 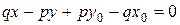 . Сопоставляя с общим уравнением прямой, получаем геометрический смысл его коэффициентов:
. Сопоставляя с общим уравнением прямой, получаем геометрический смысл его коэффициентов: 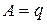 ,
, 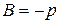 .
.
7.5
Углом между двумя прямыми 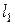 и
и 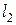 будем называть наименьший угол
будем называть наименьший угол 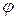 , на который надо повернуть прямую
, на который надо повернуть прямую 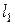 вокруг точки пересечения
вокруг точки пересечения 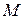 против часовой стрелки до ее совпадения с прямой
против часовой стрелки до ее совпадения с прямой 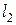
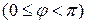 .
.
Пусть на плоскости заданы две прямые уравнениями с угловым коэффициентом:
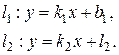
Из рисунка 7.6 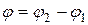 , тогда
, тогда
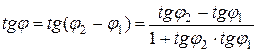 .
.
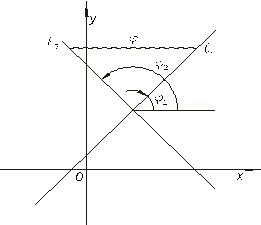
Рисунок 7.6. Угол между прямыми.
Учитывая смысл угловых коэффициентов прямой, получаем формулу для определения угла между прямыми:
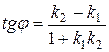 . (7.6)
. (7.6)
Если прямые 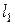 и
и 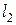 параллельны, то
параллельны, то 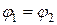 , следовательно,
, следовательно, 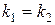 , то есть параллельные прямые имеют равные угловые коэффициенты.
, то есть параллельные прямые имеют равные угловые коэффициенты.
Если прямые 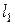 и
и 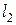 перпендикулярны, то
перпендикулярны, то 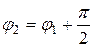 , откуда
, откуда 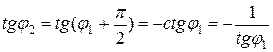 , то есть
, то есть 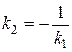 , то есть угловые коэффициенты взаимно перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
, то есть угловые коэффициенты взаимно перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
Если прямые 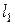 и
и 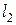 заданы общими уравнениями
заданы общими уравнениями 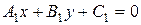 и
и 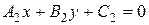 , то учитывая, что угол между прямыми совпадает с углом между векторами нормали к этим прямым, то можно указать следующую формулу для нахождения этого угла
, то учитывая, что угол между прямыми совпадает с углом между векторами нормали к этим прямым, то можно указать следующую формулу для нахождения этого угла
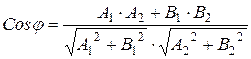 . (7.7)
. (7.7)
Тогда условие параллельности прямых
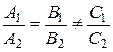 .
.
Условие совпадения прямых
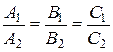 .
.
Условие перпендикулярности прямых
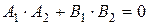 .
.
Рассмотрим ещё одну задачу для прямой. Найдём расстояние 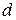 от точки
от точки 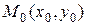 до данной прямой.
до данной прямой.
Пусть прямая 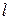 задана нормальным уравнением
задана нормальным уравнением
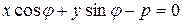 .
.
Проведем через точку 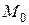 прямую
прямую 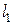 , параллельную
, параллельную 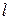 . Тогда
. Тогда 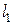 имеет уравнение
имеет уравнение 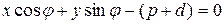 , если
, если  и
и  лежат по разные стороны от прямой
лежат по разные стороны от прямой 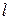 (Рисунок 7.7), или
(Рисунок 7.7), или 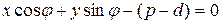 , если
, если  и
и  слежат по одну сторону от прямой
слежат по одну сторону от прямой 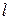 (Рисунок 7.8).
(Рисунок 7.8).
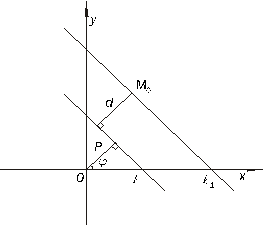
Рисунок 7.7. Расстояние от точки до прямой.
Прямая 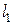 проходит через точку
проходит через точку 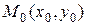 , поэтому
, поэтому 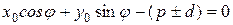 . Отсюда
. Отсюда 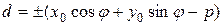 .
.
Учитывая, что расстояние всегда неотрицательная величина, получаем искомую формулу:
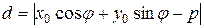 . (7.8)
. (7.8)
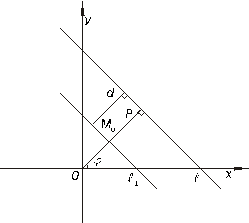
Рисунок 7.8. Расстояние от точки до прямой.
Если прямая 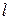 задана общим уравнением
задана общим уравнением 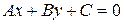 , то, учитывая связь общего уравнения с нормальным, получаем формулу для вычисления расстояния от точки до прямой:
, то, учитывая связь общего уравнения с нормальным, получаем формулу для вычисления расстояния от точки до прямой:
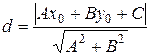 . (7.9)
. (7.9)
7.6
Исходя из геометрического смысла производной, найдём уравнение касательной к кривой 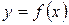 в точке с абсциссой
в точке с абсциссой 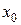 .
.
Уравнение касательной к графику функции 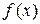 ищем в виде
ищем в виде 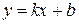 . Из геометрического смысла производной
. Из геометрического смысла производной 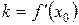 . Т.е. уравнение касательной ищем в виде
. Т.е. уравнение касательной ищем в виде 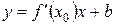 . Эта прямая проходит через точку
. Эта прямая проходит через точку 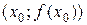 , поэтому
, поэтому 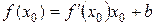 , откуда
, откуда 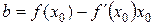 , то есть
, то есть 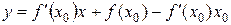 или
или
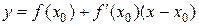 .
.
Нормалью к кривой 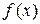 в некоторой ее точке называется перпендикуляр к касательной к этой кривой в той же точке. Если
в некоторой ее точке называется перпендикуляр к касательной к этой кривой в той же точке. Если 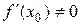 , то учитывая условие перпендикулярности прямых, уравнение нормали имеет вид
, то учитывая условие перпендикулярности прямых, уравнение нормали имеет вид
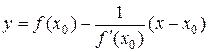 .
.
