Корреляционно-регрессионный анализ

Дисперсионный анализ

Первым этапом является формирование группировок. Для определения числа групп используем формулу Стерджесса:

,

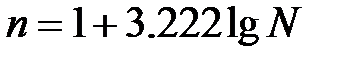где n – число групп

N – число наблюдений (судов).

Согласно исходным данным, число наблюдений составляет 89 судов. Таким образом, число групп – 7.

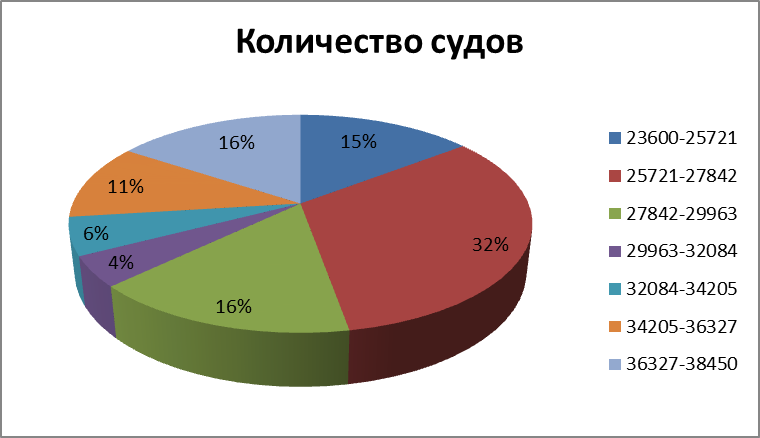
Составим таблицу, в которую запишем полученные группы, число судов в этих группах и среднюю цену судов в каждой группе (табл. 1):

Группы судов по дедвейту, тыс. т	Количество судов в группе, шт	Суммарная цена всех судов в группе, млн. долл.	Средняя цена судов в группе, млн. долл.
23600-25721		43,1	3,31
25721-27842		102,4	3,53
27842-29963		93,8	6,7
29963-32084		15,7	3,925
32084-34205		15,1	3,02
34205-36327		47,1	4,71
36327-38450		50,5	3,61
Итого		367,7

Найдем среднюю цену по рынку:

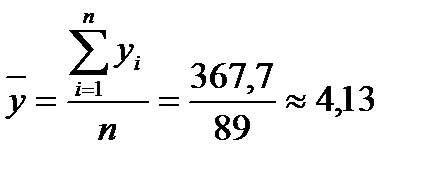млн. долл.

Для нахождения общей дисперсии используем формулу:

;

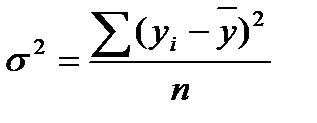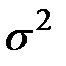
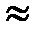7,93

Рассчитываем межгрупповую дисперсию:

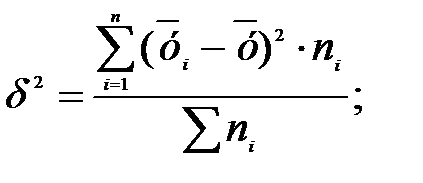
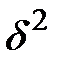
1,4

Найдем коэффициент детерминации:

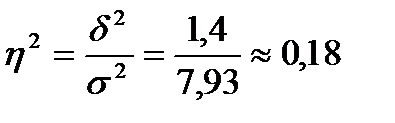
Найденный коэффициент детерминации означает, что дедвейт судна на 18% определяет изменчивость цены. Далее вычисляем корреляционное отношение, которое находится как корень из коэффициента детерминации:

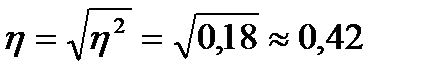
Таким образом, мы определили, что связь между дедвейтом и стоимостью судна умеренная.

Проверка значимости с помощью критерия Фишера:

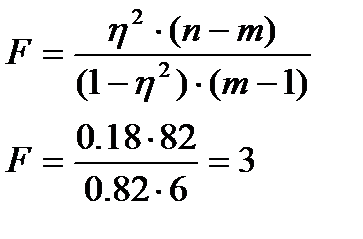
Так как 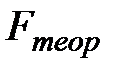≈ 2,21, то справедливо неравенство:

,

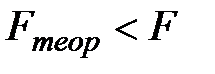что свидетельствует о том, что установленное нами корреляционное отношение является значимым.

Вывод: дедвейт исследуемых судов не сильно влияет на цену, всего на 18%. Существует множество других факторов, которые могут влиять на цену судна: страна-производитель, год постройки и тип судна. Однако, вычисленное корреляционное отношение позволяет считать связь между дедвейтом и ценой заметной. Установленное корреляционное отношение является значимым, что показывает проверка с помощью критерия Фишера.

Корреляционно-регрессионный анализ

Вычисление коэффициента корреляции:

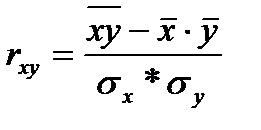
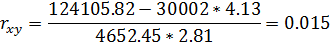
Коэффициент корреляции характеризует силу линейной связи. В данном случае 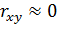, что свидетельствует о весьма слабой линейной связи.(практически отсутствует)

С помощью критерия Стьюдента оцениваем существенность коэффициента корреляции:

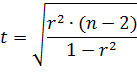
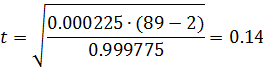
Для значения доверительной вероятности р=0,95 и количества степеней свободы f=89 t_крит=1,9867.

Справедливо равенство:

,

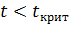т.е. найденный коэффициент корреляции не является значимым.

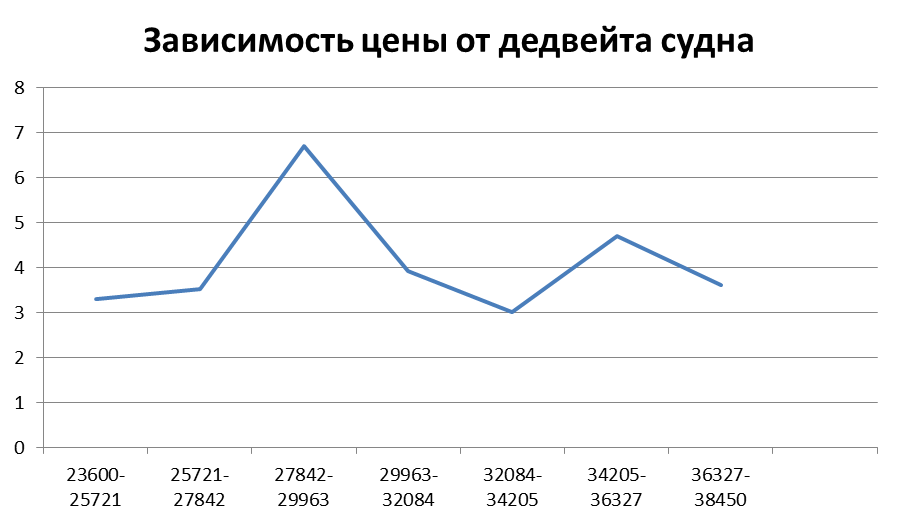
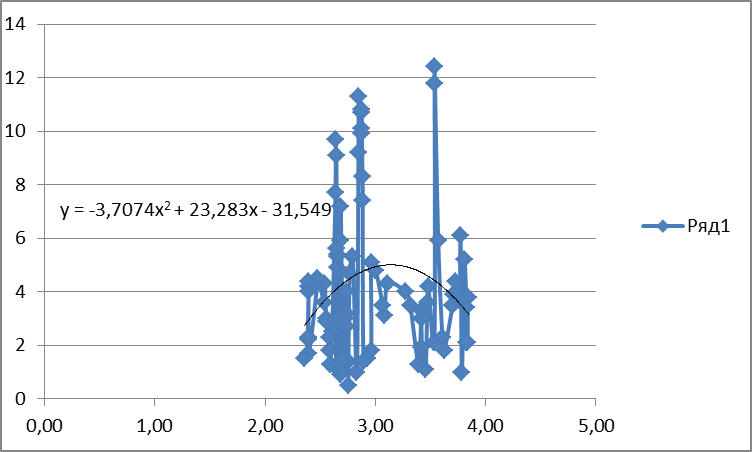
Исходя из графика зависимости стоимости судна от его дедвейта, наиболее подходящим видом связи является связь, отражаемая квадратным уравнением .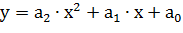

Нахождение уравнения регрессии.

В общем виде система уравнений для нахождения коэффициентов при х выглядит так:

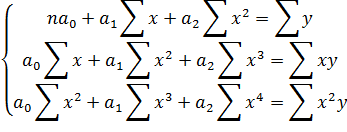
Если подставить значения х и у, при этом за х принимаем дедвейт судна деленный на 10000, для удобства вычислений, то получим:

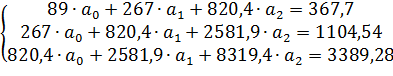
Решив систему уравнений, получим:

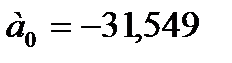
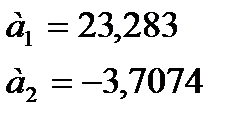
Уравнение регрессии имеет вид:

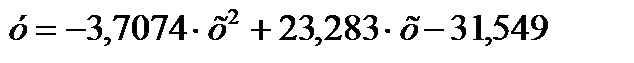
Проверка значимости уравнения регрессии производится с помощью критерия Фишера

,

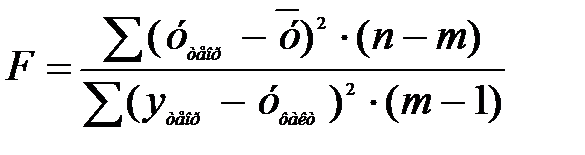
где m – число параметров уравнения регрессии (m=3)

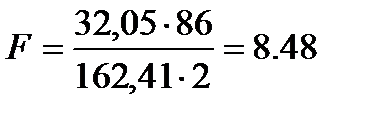
Так как 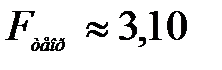, то справедливо неравенство

,

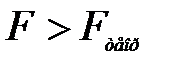следовательно, уравнение регрессии является значимым.

Министерство науки и образования, молодежи и спорта Украины

Одесский национальный морской университет

Кафедра «Системный анализ и логистика»

Расчетно-графическое задание

На тему «Исследование влияния дедвейта на стоимость судов»

Выполнил:

студент

3к. 2гр.ФТТС

Субоч Дмитрий

Проверила:

Онищенко С.П

Одесса 2011