Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид F(x,y,y^’) или y^’=f(x,y) (разрешенное относительно y).

Решением дифференциального уравнения называется функция у(x) , которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения можно записать в явном виде или в виде общего интеграла Ф(x,y,C)=0, где С – произвольная постоянная.

Теорема. Если функция f(x,y) непрерывна в некоторой области, содержащей точку (x₀,y₀) и имеет там ограниченную частную производную по y , то существует единственное решение уравнения , удовлетворяющее условию Коши: y=y₀ при x=x₀.

Уравнения, допускающие аналитическое решение:

1) Дифференциальные уравнения с разделяющимися переменными

путем деления на допускают интегрирование

.

2) Однородное дифференциальное уравнение с помощью подстановки y=xz приводится к уравнению с разделяющимися переменными .

3) Линейное дифференциальное уравнение . Решение ищем в виде , где v удовлетворяет однородному линейному дифференциальному уравнению

Для u получим уравнение .

Интегрируя последовательно уравнения для u и v получим решение

, где

4) Уравнение Бернулли . Замена приводит к линейному дифференциальному уравнению

5) Дифференциальные уравнения в полных дифференциалах

, где

Общий интеграл: , где функция u определяется из системы

Интегрируя первое уравнение, имеем . Подстановка этого выражения во второе уравнение позволяет найти функцию , а затем u.

Пример1. Решить уравнение

Решение. Так как , , то данное уравнение является уравнением в полных дифференциалах. Найдем такую функцию u(x,y), что ;

Первое из этих уравнений проинтегрируем по х , считая y постоянным; при этом вместо постоянной интегрирования поставим - неизвестную функцию от y:

Подставляя это выражение во второе уравнение, найдем

,

; .

Следовательно, можно взять и общее решение исходного уравнения будет иметь вид:

5.2. Дифференциальные уравнения высших порядков.

Общее решение дифференциального уравнения n – го порядка

,

имеет вид , где - произвольные постоянные.

Простейшие дифференциальные уравнения, допускающие понижение порядка:

1) Уравнение решается последовательным n – кратным интегрированием правой части,

2) Уравнение , не содержащее явно y, с помощью подстановки приводится к дифференциальному уравнению 1-го порядка ,

3) Уравнение , не содержащее явно x. Подстановка (y играет роль независимой переменной) с учетом равенств приводит уравнение к уравнению 1-го порядка

.

Линейное однородное дифференциальное уравнение n-го порядка( )

Общее решение линейного однородного дифференциального уравнения:

,

где - линейно-независимые частные решения (фундаментальная система решений) этого уравнения; - произвольные постоянные.

Линейное неоднородное дифференциальное уравнение n-го порядка ( )

.

Общее решение

,

где u(x)- частное решение неоднородного уравнения, а - фундаментальная система решений соответствующего однородного уравнения.

Если , то частное решение , где и - частные решения, соответствующие отдельным слагаемым и в правой части дифференциального уравнения.

1. Линейные уравнения n-го порядка с постоянными коэффициентами.

Линейное однородное уравнение n-го порядка с постоянными коэффициентами (a₀, a₁, a₂,…, a_n – числа) имеет вид:

Корни характеристического уравнения

определяют следующие слагаемые в общем решении:

а) действительный простой корень 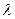дает слагаемое ;

б) действительный корень 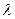кратности m дает слагаемое

.

в) пара комплексно-сопряженных корней дает слагаемое

г) пара комплексно-сопряженных корней кратности m дает слагаемое .

Например, если все корни характеристического уравнения действительны и различны, то дифференциальное уравнение имеет общее решение

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.

Если , где и - многочлены n-ой и m-ой степени, то частное решение ищут методом неопределенных коэффициентов в виде

;

Здесь r – кратность корня в характеристическом уравнении (если такого корня нет, то r = 0);

и - степени . Неопределенные коэффициенты находятся из системы линейных алгебраических уравнений, путем приравнивания коэффициентов при одинаковых степенях x в обеих частях исходного уравнения после подстановки в него u(x) вместо y. Если в выражение для f(x) входит хотя бы одна из функций или , то в u(x) надо всегда вводить обе функции.

Пример2. Решить уравнение

Решение. Составляем характеристическое уравнение ; .

- двукратный корень, - кратности 1.

Поэтому общее решение однородного уравнения имеет вид:

Правая часть исходного уравнения состоит из двух слагаемых. Для первого уравнения

(*)

частное решение будет иметь вид , так как имеем кратный корень. Подставив y₁ в уравнение (*), найдем .

Для второго уравнения (**) частное решение будем искать в виде

.

Подставив y₂ в уравнение (**), найдем

Тогда общее решение исходного уравнения y = y₀ + y₁ + y₂ , где y₀, y₁, y₂ уже найдены.

Упражнения.

5.1. Найти и построить интегральную кривую, проходящую через точку М:

a) , М (1;0);

b) , М (-2;-3);

c) , М (0;1);

d) , М (4;2);

e) , М (2;-1);

f) , М (2;1);

g) , М (1;2);

h) , М (0;1).

5.2. Найти общее решение дифференциального уравнения:

a) ; b ;

c) ; d) ;

e) ;

f) ; g ) ;

h) .

5.3. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию:

a) , ;

b) , ;

c) , ;

d) , ;

e) , ;

f) , ;

g) , ;

h) , .

5.4. Найти общий интеграл однородного уравнения:

a) ; b) ;

c) ; d) ;

e) ; f) ;

g) ; h) .

5.5. Решить линейные однородные уравнения второго порядка:

a) ; b) ;

c) ; d) ;

e) ; f) ;

g) ; h) .

5.6. Решить линейные неоднородные уравнения:

a) ; b) ;

c) ; d) .

Ряды.

Числовые ряды

Выражение называется числовым рядом;

u_{к –} общим числом ряда;

- n-ной частичной суммой ряда.

Ряд называется сходящимся, а S – суммой ряда, если . Если не существует или не ограничен, то ряд называется расходящимся.

Свойства сходящихся рядов:

1. Необходимый признак сходимости ряда: если ряд сходится, то (если , то ряд расходится).

2. Члены сходящегося ряда можно группировать в порядке следования, полученный новый ряд сходится и имеет ту же сумму.

3. Если сходятся ряды и , то сходится ряд

.

Признаки сходимости рядов с положительными членами:

1. Признак сравнения.

Если для всех >N, то из сходимости ряда следует сходимость ряда , а из расходимости ряда - расходимость ряда .

Для эффективного применения признака сравнения необходимо иметь «запас» рядов, сходимость или расходимость которых твердо установлена. Некоторые из таких рядов приведены в таблице:

Сходящиеся ряды	Расходящиеся ряды
геометрический ряд со знаменателем 0<q<1	геометрический ряд со знаменателем q 1
α >1	(0< , α=1 – гармонический ряд)
	при а>0

2. Признак сравнения в предельной форме.

Если для знакоположительных рядов и существует конечный предел , то из сходимости второго ряда вытекает сходимость первого ряда. Если (но возможно ), то из расходимости второго ряда следует расходимость первого.

3. Признак Даламбера.

Если , то при <1 ряд сходится, а при >1 – расходится.

4. Радикальный признак Коши.

Если , где k – число, то при k < 1 ряд сходится, а при k > 1 – расходится.

5. Интегральный признак Маклорена – Коши:

Ряд с общим членом u_n = f(n) сходится, если f(x) – монотонноубывающая функция, определена для всех и сходится несобственный интеграл .

Если несобственный интеграл расходится, то и ряд расходится.

Пример 1. Исследовать сходимость ряда:

Решение. Проверим выполнение необходимого признака сходимости, для чего найдем предел его общего члена:

.

Следовательно, необходимое условие сходимости выполнено. Дальнейшее исследование ряда на сходимость проведем с помощью признака Даламбера.

Вычисли , найдем:

, следовательно, по признаку Даламбера ряд сходится.

Знакочередующиеся ряды

Ряд называется знакочередующимся, если его члены попеременно то положительны, то отрицательны. Сходимость знакочередующихся рядов устанавливается с помощью признака Лейбница:

Если абсолютные величины членов знакочередующегося ряда убывают, т.е. u₁>u₂>….>u_n>… и предел его общего члена при равен нулю, то ряд сходится, а его сумма не превосходит первого члена ряда.

Сходящиеся по признаку Лейбница знакочередующиеся ряды дополнительно исследуют на абсолютную и условную сходимость.

Ряд называется абсолютно сходящимся, если он сходится по признаку Лейбница, и сходится ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если ряд сходится по признаку Лейбница, а ряд, составленный из абсолютных величин его членов, расходится.

Свойства абсолютно и условно сходящихся рядов существенно отличаются.

Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают.

Пример 2. Исследовать сходимость ряда: .

Решение. Сходимость этого знакочередующегося ряда установим с помощью признака Лейбница, для чего проверим выполнение двух условий:

1) предел общего члена ,

2) абсолютные величины членов ряда убывают, так как

Следовательно, ряд сходится.

Исследуем его на абсолютную сходимость. Для этого составим ряд из абсолютных величин данного ряда: , так как , т.е. члены данного ряда больше соответствующих членов расходящегося гармонического ряда, то по признаку сравнения ряд расходится. Поэтому, ряд - условно сходящийся.

Функциональные ряды

Функциональным рядом называется ряд , где u_n(x) – функция. Ряд называется сходящимся в точке x₀ , если сходится числовой ряд .

Совокупность , для которых функциональный ряд сходится, называется областью сходимости.

Ряд называется абсолютно сходящимся на множестве X, если на этом множестве сходится ряд .

Функциональный ряд называется равномерно сходящимся на множестве X если для любого ε >0 найдется такое N=N(ε), что для всех n>N выполняется | | < ε для всех .

Признак Вейерштрасса:

Функциональный ряд сходится на множестве X равномерно, если | u_n(x) | ≤ a_n для всех и числовой ряд сходится. Ряд называется мажорантой ряда .

Свойства равномерно сходящихся рядов:

Пусть функциональный ряд равномерно сходится для и имеет сумму S(x). Тогда справедливы теоремы:

1. Если в точке непрерывна u_n(x) , то в этой точке непрерывна функция S(x).

2. Если u_n(x) непрерывна на , то ряд можно почленно интегрировать:

3. Если u_n(x) имеют непрерывные производные и функциональный ряд сходится равномерно, то ряд можно почленно дифференцировать:

и функция непрерывна на .

Степенные ряды

Степенным рядом называется функциональный ряд, составленный из степенных функций:

Теорема Абеля: Если степенной ряд сходится при х = х_1, то он абсолютно сходится при |х |< |х₁|; если ряд расходится при x = x₂ , то он расходится при |х |> |х₂|.

Число R называется радиусом сходимости, если для |х| < R ряд сходится, а при |х| >R – расходится. Степенные ряды в интервале (-R, R) обладают всеми свойствами равномерносходящихся функциональных рядов.

Радиус сходимости R =

Степенные ряды Тейлора и Маклорена

Пусть f(x) – бесконечно дифференцируемая функция в окрестности точки x₀ . Разложение функции f(x) в ряд Тейлора:

При x=0 ряд Тейлора называется рядом Маклорена. Для разложимости f(x) в ряд Телора достаточно, чтобы для всех n , где M – некоторое число.

Разложение некоторых функций в ряд Маклорена:

Первые три ряда имеют радиус сходимости , а у остальных R=1.

Ряд Фурье.

Непрерывная функция f(x) , имеющая на интервале (-l,l) конечное число экстремумов, разлагается в ряд Фурье:

, где

;

Если f(x) – четная (нечетная) функция, то коэффициенты b_n (a_n) равны нулю.

Пример 3.Найти область сходимости степенного ряда:

Решение. Общий член данного ряда , коэффициент ряда

, следовательно, .

Определим радиус сходимости: . Интервал сходимости (-2;2). Исследуем сходимость степенного ряда на концах интервала: при х=-2 имеем знакочередующийся ряд.

или

этот ряд сходится по признаку Лейбница, так как , и абсолютные величины членов ряда убывают: ; при х=2 имеем знакоположительный ряд , или , который расходится (гармонический ряд). Таким образом, данный степенной ряд сходится в промежутке: [-2;2).

Пример 4. Используя разложение в ряд, вычислить с точностью до 0,0001.

Решение. Воспользуемся разложением в ряд Маклорена функции:

При х=-0,2 получим:

Если отбросить члены ряда, начиная с пятого, то погрешность вычисления будет по абсолютной величине меньше, чем .

Поэтому, для вычисления с заданной точностью можно ограничиться четырьмя членами ряда: .

Пример 5. Вычислить приближенно определенный интеграл: , взяв два члена разложения подынтегральной функции в ряд, и оценить погрешность вычисления.

Решение. Найдем разложение функции: в ряд, используя биномиальный ряд:

;

при m=-1/2 и, заменяя х на х³, получим:

.

Взяв только два члена разложения, получим: .

Погрешность полученного приближенного значения интеграла не превосходит по абсолютной величине третьего отброшенного члена ряда:

.

Упражнения.

6.1. Исследовать сходимость ряда с помощью признака сравнения:

a) ; b) ; c) ; d) ;

e) ; f) ; g) ; h) .

6.2. Исследовать сходимость ряда по признаку Даламбера:

a) ; b) ; c) ; d) ;

e) ; f) ; g) ; h) .

6.3. Исследовать сходимость ряда с помощью интегрального признака:

a) ; b) ; c) ;

d) ; e) ; f) .

6.4. Исследовать на абсолютную и условную сходимость знакочередующийся ряд:

a) ; b) ; c) ; d) ;

e) ; f) ; g) ; h) .

6.5. Найти область сходимости степенного ряда:

a) ; b) ; c) ;

d) ; e) ; f) ; q) .

6.6. Приложение рядов к приближенным вычислениям.

a) Вычислить ln1,3 с точностью до 0,0001, пользуясь разложением функции в ряд Маклорена y = ln (1+x).

b) Вычислить приближенно с точностью до 0,0001, пользуясь разложением функции y = (1+x)^m в ряд Маклорена.

c) С точностью до 0,0001 вычислить приближенно используя разложение подынтегральной функции в ряд Маклорена.