Определение оптимальных параметров привода
МЕТАЛЛУРГИЧЕСКИХ МАШИН
При проектировании металлургических машин приходится определять параметры привода, т.е. мощность электродвигателя и передаточное число редуктора. При этом необходимо стремиться к оптимизации данных параметров.
В общем виде любая машина может быть представлена как совокупность трех компонентов (рисунок 18): двигатель (Д), передаточное устройство (ПУ) (редуктор), ведомое звено (ВЗ) (рабочий орган). Характеристиками указанных компонентов являются:
Мн – номинальный момент двигателя;
Iд – момент инерции якоря двигателя;
i – передаточное число редуктора;
Мв – момент статических сопротивлений, приложенный к ведомому звену;
Iв – момент инерции ведомого звена.
 |
Рисунок 18 - Структурная схема машины
При проектировании машины неизвестными являются параметры двигателя и редуктора - Мн, Iд, i. Момент инерции двигателя Iд может быть связан с его номинальным моментом Мн эмпирической зависимостью [8]:
Iд = А Мнс ,
где А, с – константы, приведенные в литературе [8].
Таким образом, число неизвестных параметров уменьшается до двух - Мн, i. Для нахождения указанных параметров обычно задаются некоторыми условиями на проектирование машины [8], которым соответствуют уравнения, выводимые из дифференциального уравнения движения машины. Рассмотрим решение задачи для машин кратковременного и повторно-кратковременного режима работы, для которых наиболее распространенными условиями на проектирование являются: “Ускорение ведомого звена задано”, “Рабочее время цикла должно быть минимальным”. Указанным условиям соответствует система уравнений:
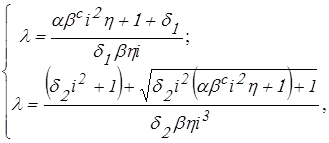 (41)
(41)
где l – средняя кратность пускового момента двигателя Мп, 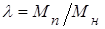 ;
;
b – отношение номинального момента двигателя к моменту статических сопротивлений, приложенных к ведомому звену, 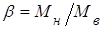 ;
;
a, d1, d2 - константы, зависящие от параметров ведомого звена и двигателя;
h - кпд механизма.
В уравнениях (41) три неизвестные величины l, b, i, поэтому для их нахождения поступают следующим образом. Предварительно выбирают тип двигателя, для которого по данным [8] задаются значением средней кратности пускового момента двигателя l=l0. Тогда, двух уравнений (41) достаточно для определения двух величин b, i. Далее приравниваются правые части уравнений (41), решая которые приходят к одному уравнению вида b=f(i).
Выполним описанные действия. Введем обозначение:
B = abci2h ,
т.е. 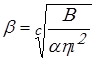 . (42)
. (42)
Тогда, приравнивая правые части уравнений (41) с учетом (42) получаем:
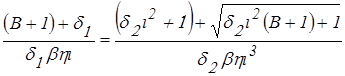 . (43)
. (43)
После сокращения на bhi и умножения на d1d2i2 выражение (43) принимает вид:
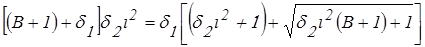 .
.
Раскрываем скобки и упрощаем:
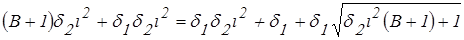 ;
;
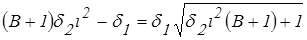 ;
;
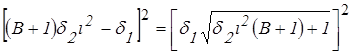 ;
;
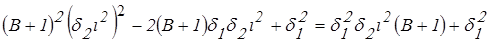 ;
;
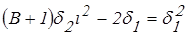 ;
;
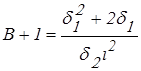 ;
;
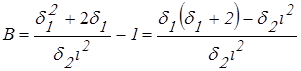 ;
;
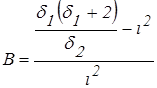 .
.
Тогда, с учетом (42) получаем зависимость b=f(i):
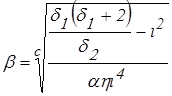 . (44)
. (44)
Полученное уравнение (44) и любое из уравнений (41) образуют систему вида:
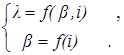
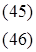
поиск решения которой выполняется методом последовательных приближений (метод итераций) [8].
Метод последовательных приближений заключается в следующем. Значение передаточного числа i изменяется от нижнего предела iн до верхнего предела iв с шагом Di. При этом на каждом шаге по уравнению (46) вычисляется значение b, а по уравнению (45) – значение l. Процесс вычисления повторяется до тех пор, пока полученное значение l не приблизится к заданному значению l0 с принятой степенью точности e. Найденное при этом значение передаточного числа редуктора будет являться оптимальным i0.
Нижнее предельное значение iн передаточного числа можно принять равным 1. Верхнее предельное значение iв определяется из (44). Так как отношение номинального момента двигателя к моменту статических сопротивлений, приложенных к ведомому звену, b есть величина положительная (b> >0), то, исходя из уравнения (44):
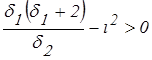 .
.
Тогда, верхнее предельной значение iв передаточного числа равно
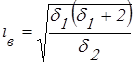 .
.
Степень точности e решения зависит от величины шага Di, поэтому удобно начинать поиск решения с большого шага Di = (iв - iн)/10, а далее при необходимости уменьшать шаг Di. Степень точности e можно принимать из ряда 0,1; 0,01; 0,001 и т.д.
Графическая интерпретация метода последовательных приближений приведена на рисунке 19. Блок-схема алгоритма решения представлена на рисунке 20 .
После ввода исходных данных переменной i присваивается значение iн, вычисляются значения величин b и l1. Далее текущее значение i увеличивается на шаг Di и проверяется условие достижения верхнего предела iв. Если iв достигнуто, а значения i0 и b0 не найдены, то выдается сообщение “Решения нет”.
Если iв не достигнуто, то для текущего значения i вычисляются значения величин b и l.
Найденное текущее значение l может быть больше или меньше заданного значения l0. Поэтому для проверки перехода через значение l0 используются две переменные h и g. Переменная h – это разность между предыдущим значением l1 и заданным значением l0 кратности пускового момента l. Переменная g – это разница между текущим и заданным значением кратности, т.е. l-l0. Если предыдущее и текущее значения кратности l находятся по одну сторону от заданного значения l0, то произведение разностей h×g будет положительным, в противном случае – отрицательным.

а б
а - b = f(i) ; б - l = f(b, i)
Рисунок 18 – Графическая интерпретация метода последовательных приближений
Если произведение разностей h×g положительно, то переприсваивается предыдущее значение кратности l, и цикл вычислений, описанных выше, повторяется. В случае, когда произведение h×g стало отрицательным, т.е. произошел переход текущего значения lчерез l0, выполняется проверка достижения значения l0 с принятой степенью точности e. Если степень точности не достигнута, то происходит возврат к предыдущему значению i, шаг Di уменьшается и циклические вычисления b и l повторяются.
При достижении принятой степени точности e текущие значения i, b, l являются решением уравнений (45)-(46) и определяют оптимальное передаточное число i0 редуктора и соответствующие ему отношение b0 и кратность l0.
Систему уравнений (45)–(46), соответствующих принятым условиям проектирования машины, можно решить и одним из численных методов поиска корней уравнений, рассмотренных в разделе 4.
Для этого в уравнение (45) необходимо вместо b подставить выражение (46) и привести первое к виду F(i)=0.
Для рассматриваемых условий уравнение F(i)=0 принимает вид:
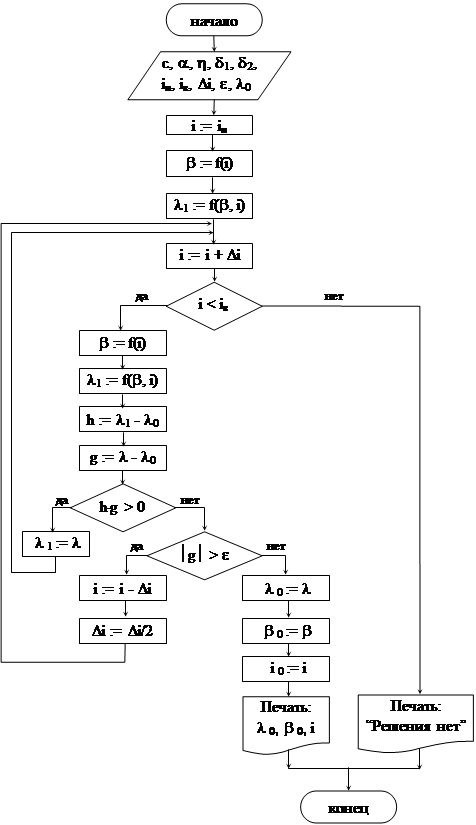
Рисунок 19 - Блок-схема алгоритма метода последовательных приближений
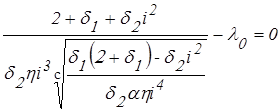 . (47)
. (47)
Корнем уравнения (47) является оптимальное передаточное число редуктора i0. В качестве интервала локализации корня принимается диапазон [iн; iв]. Для решения уравнения (47) лучше всего использовать метод деления отрезка пополам (31)–(34), блок-схема алгоритма которого приведена на рисунке 12. По найденному значению i0 по выражению (44) вычисляется значение b0.
