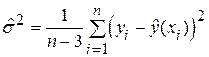Орреляционный и регрессионный анализ.

4.1. Общие понятия.

Основной задачей корреляционного (или регрессионного) анализа является построение статистической модели связи между различными величинами (параметрами) и получение метода косвенного оценивания одних параметров через другие, которые измеряются раньше по времени или значения которых измерить проще (дешевле). Попутно, при необходимости, решаются задачи прямого оценивания характеристик генеральной совокупности (см. предыдущий раздел), проверки статистических гипотез (см. следующий раздел). Корреляционный и регрессионный анализ является частью статистического анализа. Изучению могут подлежать параметры, измеряемые как в шкалах отношений или интервалов, например, физиологические параметры человека (рост, вес, температура тела и т.д.), экономические показатели предприятий и пр., так и в шкале порядка.

В задачах корреляционного и регрессионного анализа в общем случае предполагается, что имеется некоторая величина (обозначим ее y), которая существенно зависит от m параметров (факторов) x₁,x₂,…,x_m (среди них может быть время) и несущественно – от множества других факторов, которые не подлежат измерению и представляются как случайные. При одних и тех же значениях x₁,x₂,…,x_m величина y может принимать разные значения, т.е. она является случайной и поэтому будет обозначаться Y. Предполагается, что величина Y при любых значениях x₁,x₂,…,x_m является суммой двух составляющих: детерминированной и случайной, которую обозначим ε. Все неизвестные и случайные факторы объединены в этой случайной аддитивной составляющей, причем предполагается, что случайная величина e при любых значениях x₁,x₂,…,x_m имеет нулевое математическое ожидание: Мε=0. Таким, образом,модель связи между параметрами Y, x₁,x₂,…,x_m, которую называют регрессионной моделью, имеет вид:

,

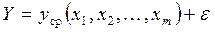где 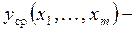некоторая детерминированная (обычная) функция, являющаяся условным математическим ожиданием случайной величины Y и называемая уравнением регрессии, e – случайная величина, вид распределения которой должен быть задан, причем Мε=0 (чаще всего принимается e ~ N(0,σ²)).

Дисперсия De º s ² равна дисперсии 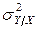условного распределения 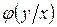и, вообще говоря, может быть функцией от вектора x. Вид распределения 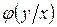тот же, что и для случайной величины e.

Пример. Цена Y на некоторый вид товара в условиях свободного ценообразования зависит, во-первых, от среднего спроса, цен на товары, являющиеся сырьем, комплектующими или конкурирующими с данным (первое слагаемое), а во-вторых, от массы других слабо влияющих, неизвестных и случайных факторов. Качественные признаки, измеряемые в шкале наименований (название региона, населенного пункта, престижность района города, магазина, и др.), должны быть фиксированы или считаться случайными факторами, входящими в e.

Для построения регрессионной модели используются результаты испытаний (наблюдений), которые можно представить в виде n точек (m+1)-мерного пространства: (y₁, x₁₁,x₂₁,…,x_m1), (y₂, x₁₂,x₂₂,…,x_m2),…, (y_n, x_1n,x_2n,…,x_mn).

Особенность корреляционного анализа по сравнению с регрессионным заключается в том, что он имеет дело только с двумерной или многомерной случайной выборкой (матрицей) из определенной генеральной совокупности, характеризуемой (m+1) случайными величинами 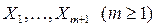, причем любой из этих параметров формально может быть взят в качестве зависимой переменной y.

Регрессионный анализ осуществляется при наличии смешанных данных: значения одной группы параметров задаются исследователем (в частности, моменты времени или точки пространства для измерения параметров второй группы) и измеряются достаточно точно, значения другой группы в общем случае рассматриваются как реализации случайных величин при одних и тех же значениях параметров первой группы. При этом можно строить самые различные регрессионные модели, с включением в модель всех параметров или только части.

Корреляционный анализ занимается обработкой данных так называемого пассивного эксперимента, а регрессионный – активного.

Методы построения регрессионной модели в регрессионном и корреляционном анализе одинаковы. Разной является лишь интерпретация некоторых оцениваемых величин.

Построение точной регрессионной модели невозможно, так как на основе ограниченных данных нельзя точно определить функцию 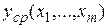. Можно определить только оценку условного математического ожидания 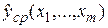, называемую эмпирическим уравнением регрессии. Оценка должна быть состоятельной: чем больше объем выборки, тем точнее должна быть регрессионная модель. Эту оценку, как случайную величину, будем обозначать 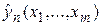, Тогда Y при каждом наборе x₁,x₂,…,x_m будет являться суммой двух случайных величин:

.

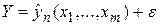Поэтому регрессионная модель обычно ищется в виде:

,

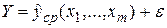где 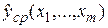– детерминированная функция, являющаяся оценкой условного математического ожидания случайной величины Y, для которого должен быть найден также доверительный интервал:

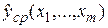–Δ₁(x₁,x₂,…,x_m)< 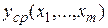< 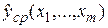+Δ₂(x₁,x₂,…,x_m);

e – случайная величина, распределенная по заранее определенному закону с Мε=0 и дисперсией .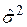

Задача корреляционного (регрессионного) анализа сводится к оценке параметров функции 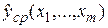определенного (предполагаемого) класса, доверительного интервала, дисперсии σ²,а также – к определению толерантного интервала для индивидуального значения y в случае, когда будут измерены только x₁,x₂,…,x_m. При необходимости осуществляется проверка статистических гипотез о значимости связи, постоянстве дисперсии σ²и др. В линейном корреляционном анализе оценивают также показатели статистической зависимости между параметрами: ковариации, коэффициенты парной, множественной и частной корреляции (при измерениях в шкале порядка используется понятие ранговой корреляции). В нелинейном корреляционном анализе оценивают корреляционные отношения. В регрессионном анализе таких понятий нет, здесь пользуются более общим термином: коэффициент детерминации (об этом – позднее).

Из регрессионной модели не следует, что является причиной, а что следствием. Установление причинно-следственных связей – отдельная проблема, выходящая за рамки математической статистики.

Частным случаем регрессионной модели при определенных условиях является модель статистической зависимости между параметрами, представляющими временной ряд. Она имеет вид:

,

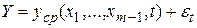где t – время, причем, обычно предполагают, что измерения параметров y,x₁,…x_m-1 производятся через равные промежутки времени: t=1,2,3,…n. Временным рядом называют измерения, представленные в виде n m-мерных векторов, упорядоченных по возрастанию величины t. Модель временного ряда является частным случаем регрессионной модели тогда, когда ε_t является случайной величиной. Если же ε_t – случайный процесс (см. ч.3), то и Y≡Y(t) – случайный процесс. Временные ряды могут быть выражены также авторегрессионными моделями, которые исключают из рассмотрения время t. Частным случаем модели временного ряда являются трендовые модели:

.

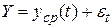Построение многофакторных регрессионных моделей, по сути, немыслимо без использования компьютерных программ. Одним из пакетов программ, которыми можно пользоваться для этой цели, является Система статистического анализа (SAS).

Регрессионные модели используются в задачах прогнозирования, разработки и принятия решений, управления. Регрессионные модели могут быть использованы, в частности, для выявления фактов, не укладывающихся в рамки модели и требующих специального анализа, например, фактов нарушений регламентированных законом процессов человеческой деятельности.

4.2. Методы построения однофакторных регрессионных моделей.

Пусть имеются результаты измерений некоторых параметров х, y в виде n точек: 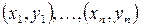. В таком виде всегда можно представить и сгруппированные в таблицу данные, когда указывается частота повторения различных пар значений x,y. Результаты измерений могут быть получены двумя способами: на основе пассивного и активного экспериментов.

При пассивном эксперименте точки (x_i, y_i) считаются векторами значений системы случайных величин X, Y, а вся совокупность точек – случайной выборкой из некоторой генеральной совокупности. Например, X и Y – показатели твердости и прочности изделий случайной выборки объема n из партии продукции или доход и количество автомобилей на душу населения в n городах, взятых наугад среди всех городов страны с определенными признаками. Это могут быть также цены на товары-субституты, зафиксированные в n моментов времени, взятых в течение года на одном рынке (если эти цены можно считать случайной выборкой из некоторой гипотетической генеральной совокупности). В случае пассивного эксперимента обычно, прежде всего, оценивают коэффициент корреляции. Это позволяет сразу решить, имеет ли смысл строить регрессионную модель.

При активном эксперименте значения одного из параметров (обычно x) задает исследователь, другие условия опытов (наблюдений) оставляют без изменений, а значения другого параметра рассматривают как значения случайной величины, являющиеся представителями разных генеральных совокупностей при разных значениях х. Например, – наблюдения за ценой (Y) на определенный товар и на определенном рынке в разные моменты времени (х). Другой пример: результаты испытаний на прочность (Y) образцов заготовок деталей при задаваемых значениях температуры режима термообработки (х), если другие параметры режима термообработки оставляют без изменения. В первом примере при одном и том же значении параметра х нельзя провести несколько опытов (наблюдений), во втором – можно. Такое различие может быть учтено при обработке данных.

Однофакторную регрессионную модель (на плоскости) строят в виде:

Y= 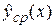+e ,

где 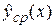= 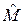[Y/x] – оценка условного математического ожидания случайной величины Y (при фиксированном значении х), для которого должен быть найден также доверительный интервал (далее для краткости будем писать ):

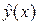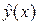– Δ₁(x)< 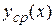< 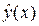+ Δ₂(x);

e – случайная величина, распределенная по заранее определенному закону с Мε=0 и дисперсией De, в качестве которой берут точечную оценку .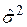

Данные 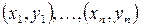желательно нанести на координатную плоскость. Тогда легче подбирать вид эмпирического уравнения регрессии 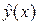, а также делать заключение относительно постоянства дисперсии De .

Выбор вида условного распределения 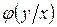осуществляется экспертами на основе привлечения более широкой информации, чем данные об n точках. Методы определения вида и параметров 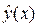основаны на использовании различных критериев близости точек к кривой 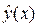. Выбор критерия зависит от распределения 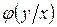. В качестве критериев выбирают, например, сумму квадратов расстояний от точек до кривой, сумму модулей отклонений этих точек от кривой и другие. Но чаще всего используется метод наименьших квадратов, вытекающий из предположения о нормальном законе распределения .

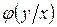Метод наименьших квадратов состоит в оценивании параметров функции 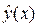заданного вида на основе критерия минимума суммы квадратов отклонений значений y_i от соответствующих точек на кривой. В этом случае метод наименьших квадратов сводится к решению задачи определения минимума функции, т.е.

,

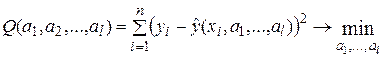где a₁,…,a_l – неизвестные параметры.

Для решения этой задачи, надо найти l частных производных и приравнять их к нулю, затем – решить полученную систему l уравнений с l неизвестными:

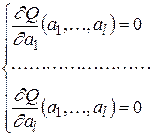
Таким образом будут найдены точечные оценки параметров функции .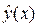

Метод наименьших квадратов равносилен критерию минимума дисперсии De, если она постоянна.

Оценка дисперсии De, если ее можно считать постоянной,имеет вид:

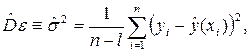
где l – число оцениваемых параметров функции .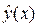

Величина 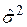оказывает основное влияние на точность оценки величины Y (индивидуального значения) по значению x. Она используется также при нахождении доверительного интервала для M[Y/x]. В случае нормального распределения 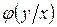половина длины доверительного интервала определяется по формуле:

,

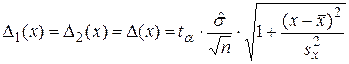где t_α– квантиль распределения Стьюдента с (n–l) степенями свободы, соответствующий доверительной вероятности 1– a , .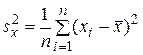

Нетрудно убедиться, что с увеличением объема испытаний n длина доверительного интервала уменьшается в пределе до 0. Поэтому объем испытаний стараются выбрать таким, чтобы 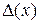не оказывало существенного влияния на точность оценки величины Y (индивидуального значения) по значению x.

Если De зависит от х, то область, в которой находятся значения х_i , разбивают на несколько интервалов, для каждого из которых вычисляют оценки дисперсий, после чего производят аппроксимацию функции 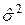(х) примерно так же, как строят эмпирическое уравнение регрессии.

4.2.1. Метод наименьших квадратов для линейной и

экспоненциальной зависимостей.

Предположим, что уравнение регрессии – линейная функция: 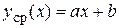, где a и b неизвестные параметры, которые надо оценить на основе данных об n точках 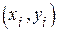. Тогда

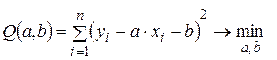
Находятся частные производные и приравниваются к нулю:

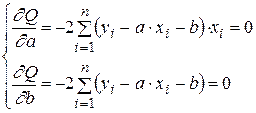или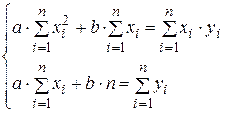

Умножая первое уравнение на 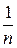, а второе – на 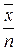, решая эту систему и вводя обозначения:

,

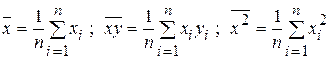получим оценки коэффициентов:

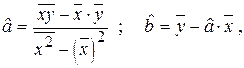
где 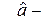эмпирический коэффициент регрессии.

Оценки 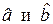являются несмещенными, эффективными (в классе линейных оценок) и обычно (если 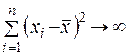при n 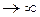) состоятельными.

В регрессионном анализе несмещенность и эффективность (при n = const ) понимается в том смысле, что x_i берутся одними и теми же, так что параметры уравнения регрессии могут сильно зависеть от выбора x_i .

В корреляционноманализе x_i – это значения случайной величины X, поэтому выражения:

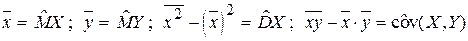
здесь имеют конкретный статистический смысл: они являются оценками математических ожиданий, дисперсии, ковариации. В регрессионном анализе такого смысла они не несут. Умножение оценок дисперсии и ковариации на 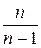делает их несмещенными, но оценка 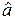от этого не изменится, т.е. она несмещенная в любом случае. Учитывая, что 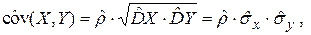где 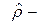оценка коэффициента корреляции, а 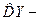оценка дисперсии случайной величины Y , эмпирический коэффициент регрессии можно выразить иначе:

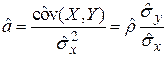
Эмпирическое уравнение регрессии удобнее записывать в виде:

,

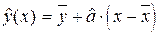поскольку при 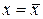для величины 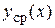будет иметь место самый узкий доверительный интервал. Вообще доверительный интервал для условного математического ожидания случайной величины Y имеет вид (рис. 16):

,

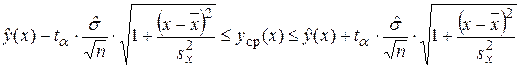где 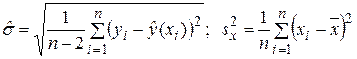, , 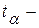квантиль распределения Стьюдента с (n–2)–мя степенями свободы, соответствующий доверительной вероятности 1– a .

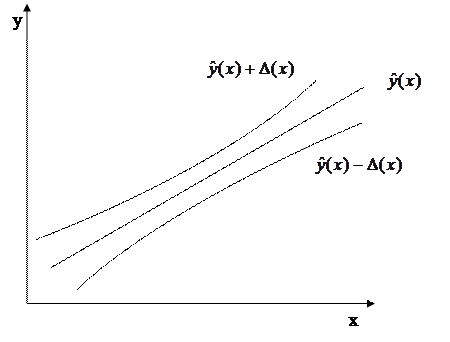
Рис.16. Графики эмпирического уравнения регрессии и доверительных границ для условного математического ожидания M[Y/x].

В случаях, когда 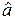близко к нулю, необходимо проверять гипотезу H₀: а=0 против гипотезы H₁: а¹ 0. Если будет принята гипотеза H₀ , то это будет равносильно признанию независимости величины y от фактора x.

Описанный метод наименьших квадратов используется также для логарифма экспоненциальной зависимости: 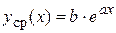, поскольку после логарифмирования этой функции будет иметь место линейная функция.

4.2.2.Метод наименьших квадратов для параболы

Пусть 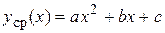. Тогда

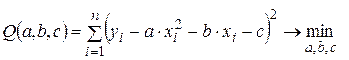
Находятся частные производные и приравниваются к нулю:

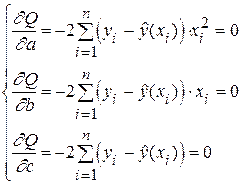или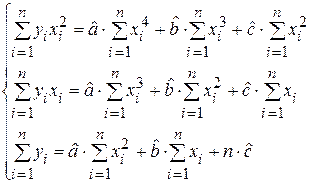

Коэффициенты 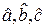находятся из этой системы уравнений.

Оценка дисперсии условного распределения: