Линейный регрессионный анализ

Если исследуемые случайные величины подчиняются закону Гаусса и, кроме того, являются зависимыми (то есть между ними имеются стохастические связи), то с изменением одной величины в общем случае могут меняться все статистики другой случайной величины. В частном случае, когда рассматриваются только два параметра из этих статистик, можно записать:

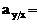ƒ₁ (х) , (2.10)

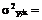ƒ₂ (х) . (2.11)

Первую зависимость называют уравнением теоретической линии регрессии, а вторую – скедастической зависимостью (здесь и далее для упрощения рассматривается только регрессия Y по X).

Линейный регрессионный анализ результатов испытаний включает оценку коэффициентов уравнения эмпирической линии регрессии и ее графическое построение с учетом скедастической зависимости, а также проверку гипотезы о соответствии выбранной функции (2.10) данным ______________________________________________________________

* Курсивом (здесь и далее) дан текст для более глубокого изучения темы.

опыта. Эта гипотеза называется гипотезой адекватности выбранной математической модели. При линейном регрессионном анализе принимается простейшая математическая модель – линейная функция. Эмпирическая линия регрессии при этом, естественно, служит лишь некоторым приближением к теоретической линии регрессии (тем лучшим, чем больше объем эмпирической выборки). Для разных выборок, т. е. в различных сериях экспериментов, коэффициенты уравнения выбранной функции будут отличаться. Таким образом, в опытах можно получить множество эмпирических линий (число которых равно числу серий экспериментов), образующих некоторую область вокруг неизвестной теоретической линии. Теоретическую линию регрессии не удается установить точно, вследствие ограниченности объема каждой выборки.

Обычно регрессионному анализу предшествует корреляционный, на основании которого производят оценку средних значений изучаемых величин, а также их выборочных дисперсий и выборочного коэффициента корреляции ( 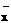, , 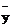, , 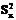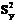r). После этого уравнение эмпирической линии регрессии, являющейся, как указано, лишь некоторым случайным приближением к теоретической линии регрессии, записывают для принятой модели в виде:

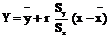. (2.12)

При малом объеме выборки (число пар экспериментальных величин n ≤ 50) для упрощения анализа можно принять, что дисперсия случайной величины Y не зависит от х, то есть скедастическая зависимость (2.11) имеет вид:

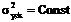. (2.13)

В этом случае все параметры уравнения (2.12) могут быть определены по формулам (2.1)…(2.5). Кроме того, если имеется n пар экспериментальных величин (x₁, y₁), (x₂, y₂)…(x_n, y_n), то в качестве оценки дисперсии Y вместо 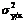может быть использована выборочная дисперсия

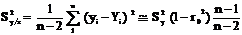. (2.14)

Величина 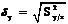(2.15)

используется в первом приближении как мера рассеяния экспериментальных значений Y вокруг линии регрессии, т. е. как ошибка определения эмпирической линии регрессии по уравнению (2.12).

Более точный подход заключается в оценке зоны вероятного расположения теоретической линии регрессии. Для этого с принятой вероятностью, которая определяется выбранным (или заданным) уровнем значимости α, строится доверительный интервалеерасположения. Процедура такого построения заключается в следующем. Для ряда значений x по формуле (2.12) в случае принятия линейной гипотезы находят величину Y, а также её дисперсию:

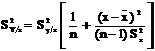. (2.16)

Далее составляют доверительный интервал для :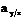

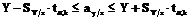, (2.17)

где t_α,k – значение квантили статистики t распределения Стьюдента для вероятности P. Значения t_α,k приведены в табл. 2.3, где число степеней свободы рассчитывается по формуле: k = n – 2. Затем для дискретных значений x_i , задаваемых с выбранным шагом Δx, согласно условию (2.17) строят нижнюю и верхнюю границы доверительного интервала. Очевидно, что такое приближенное построение будет тем точнее, чем меньше шаг Δx.

Таблица 2.3

Значения α-пределов t_α,k распределения Стьюдента в зависимости от k

при k > 30 t_α,k = Z_p; (см. табл. 2.2)

k	Α
		0,100	0,050	0,025	0,010
		6,314 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 1,812 1,782 1,761 1,746 1,734 1,725 1,717 1,711 1,706 1,701 1,697	12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,179 2,145 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,042	25,452 6,205 4,177 3,495 3,163 2,969 2,841 2,752 2,685 2,634 2,550 2,510 2,473 2,445 2,423 2,405 2,391 2,379 2,369 2,360	63,657 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,055 2,977 2,921 2,878 2,845 2,819 2,797 2,779 2,763 2,750