Метод Гаусса (исключения неизвестных)

Раздел 3. Численные методы решения уравнений

Виды математических моделей (уравнений) в теории электрических цепей

1. 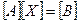-системы линейных алгебраических уравнений –

линейные цепи постоянного и синусоидального переменного (комплексный метод) тока.

2. 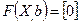- системы нелинейных алгебраических или

трансцендентных уравнений – нелинейные цепи постоянного или синусоидального тока.

3. 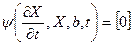. –системы нелинейных дифференциальных

уравнений первого порядка в обыкновенных производных – переходные процессы в нелинейных цепях.

Здесь F и ψ – вектор-функции, т.е. 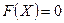эквивалентно записи:

f₁(X,b₁) = 0

f₂(X,b₂) = 0

…………

f_n(X,b_n) = 0

а 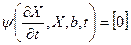-записи:

ψ₁(dX/dt,X,b₁,t) = 0

ψ₂(dX/dt,X,b₂,t) = 0

…………………..

ψ_n(dX/dt,X,b_n,t) = 0

Рассмотрим наиболее эффективные методы решения этих уравнений.

Численные методы решения систем линейных алгебраических уравнений (ЛАУ)

Метод Гаусса (исключения неизвестных)

Методы решения ЛАУ имеют важное значение, так как они применяются (итерационно) для решения более сложных уравнений.

Пусть система ЛАУ задана в виде:

,

,

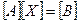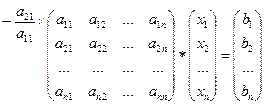где 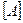- квадратная матрица n – го порядка с ненулевыми диагональными элементами 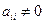; 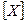- вектор неизвестных; 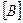- вектор правых частей.

Алгоритм метода Гаусса состоит из прямогои обратного хода. Во время прямого хода осуществляется последовательное исключение неизвестных. Система приобретает вид:

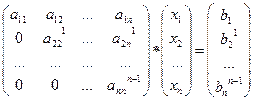
Пересчет коэффициентов производится по формуле:

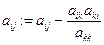, где i, j = k+1, …n при исключение k-го неизвестного.

При этом столбец правых частей 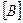удобно рассматривать как n + 1 столбец матрицы коэффициентов 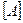, т.е. j = k+1, …n+1.

Обратный ход заключается в определении неизвестных, начиная с последнего уравнения где осталась одна неизвестная x_n. Полученное значение x_n подставляется в предыдущее уравнение и определяется x_n-1 и т.д.

Для произвольного x_k получается следующая формула:

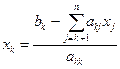
где k = n, n -1,…1.

Трудоемкость метода Гаусса оценивается количеством выполняемых арифметических операций:

.

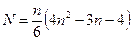Кубическая зависимость от размерности задачи существенно ограничивает сложность анализируемых цепей. Однако если часть коэффициентов a_ik в матрице 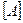равна нулю, т.е. она является разреженной, то появляется возможность сокращения трудоемкости.

Основная идея метода разреженных матриц состоит в учете при вычислениях и хранении только ненулевых элементов матрицы 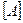. Степень разреженности матрицы характеризуется коэффициентом заполнения:

;

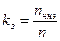где n_ннэ –число ненулевых элементов.

Существуют матрицы коэффициентов специального вида: ленточные, когда ненулевые элементы располагаются вдоль главной диагонали; и блочно-диагональные, когда вдоль главной диагонали располагаются ненулевые блоки. Еще встречаются блочно-диагональные с окаймлением.

Пример ленточной матрицы Пример блочно-диагональной матрицы

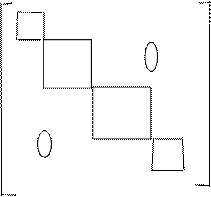Пример блочно-диагональной матрицы с окаймлением

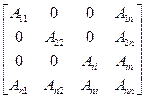
Для них разработаны специальные эффективные методы решения. Для диагональной – метод прогонки. Блочная распадается на отдельные группы уравнений по блокам, которые решаются методом Гаусса. Для блочно-диагональных с окаймлением существуют диакоптические методы решения.

Диакоптика – подход к исследованию сложных систем, заключающейся в расчленение системы на части и её анализе по частям при учете всех связей между выделенными частями.