Решение системы линейных уравнений методом Гаусса (последовательного исключения неизвестных)
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное – просто!Кстати, портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Про миноры и алгебраические дополнения можно на время забыть! Необходимо уметь складывать и умножать!Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах.
Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и мы постараемся в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любойсистемы линейных уравнений. Как мы помним, правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случаеприведет нас к ответу! На данном уроке мы вновь рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№ 2-3 отведена статья Несовместные системы и системы с общим решением. Заметим, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе
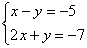 и решим ее методом Гаусса.
и решим ее методом Гаусса.
На первом этапе запишем так называемую расширенную матрицу системы:
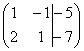 .
.
По какому принципу записаны коэффициенты, думаем, всем видно.
Примечание: Расширенная матрица системы получается из исходной с помощью «операции наращивания строк / столбцов». В данном случае матрицу нарастили за счёт столбца свободных членов исходной системы уравнений.
Примечание: Кроме перечисленных ранее 6-и алгебраических операций с матрицами и «операции наращивания» существует ещё «операция отбрасывания строк/столбцов». С помощью «операции отбрасывания строк/столбцов» составляют, например, подматрицы, определители которых являются минорами элементов матрицы.
Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто линия отчёркивания для удобства оформления.
Определение:Матрица системы – это матрица, составленная только из коэффициентов при неизвестных переменных системы линейных уравнений.
Определение:Расширенная матрица системы – это матрица системы, которую нарастили справа на столбец свободных членов.
В данном примере 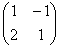 . – это матрица системы, а
. – это матрица системы, а 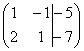 - это расширенная матрица системы. Любую из них можно для краткости называть просто матрицей.
- это расширенная матрица системы. Любую из них можно для краткости называть просто матрицей.
После того, как записана расширенная матрица системы, с ней необходимо выполнить некоторые новые алгебраические действия, которые с лёгкой руки Гаусса называются также элементарными преобразованиями матрицы. Преобразования называют элементарными, потому что показано (будем считать это определением), что
Определение: После каждого элементарного преобразования расширенной матрицы получается совершенно другая матрица, но решения для этой новой системы линейных уравнений остаются теми же, что и для исходной матрицы.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
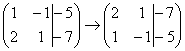
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
Рассмотрим, например матрицу  . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:
. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:
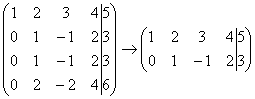 .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не будем, понятно, нулевая строка – это строка, в которой одни нули.
4) Строку матрицы можно умножить (разделить)на любое число, отличное от нуля. Рассмотрим, например, матрицу 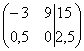 . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 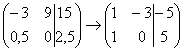 . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
Рассмотрим нашу матрицу из практического примера: 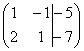 . Сначала распишем преобразование очень подробно.
. Сначала распишем преобразование очень подробно.
Умножаем первую строку на (-2): 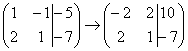 , далее ко второй строке прибавляем первую строку, оставляя первую без изменений:
, далее ко второй строке прибавляем первую строку, оставляя первую без изменений: 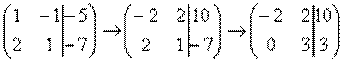 . Теперь первую строку можно разделить «обратно» на (–2):
. Теперь первую строку можно разделить «обратно» на (–2): 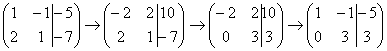 .
.
Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На практике так подробно, конечно, не расписывают, а пишут короче:
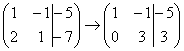
Еще раз: ко второй строке прибавили первую строку, умноженную на (–2). Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: 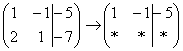 »
»
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 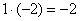 , и ко второй строке прибавляю первую: 2 + (–2) = 0.
, и ко второй строке прибавляю первую: 2 + (–2) = 0.
Записываю результат во вторую строку: 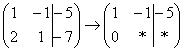 »
»
«Теперь второй столбец. Вверху –1 умножаю на –2: (-1∙(-2) = 2). Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:
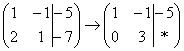 »
»
«И третий столбец. Вверху –5 умножаю на –2: (-5∙(-2) = 10). Ко второй строке прибавляю первую: (–7 + 10 = 3). Записываю результат во вторую строку:
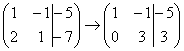 »
»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
