Вопрос 11. Решение АЛСУ методом Гаусса. (последовательного исключения неизвестных).

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу!.

Вернемся к простейшей системе
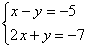и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы:
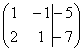. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 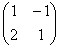. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 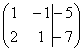. Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: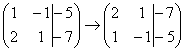

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .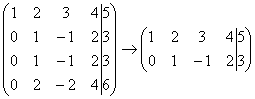

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 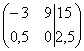. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 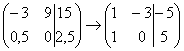. 5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 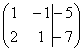. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 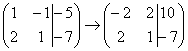, и ко второй строке прибавляем первую строку умноженную на –2: 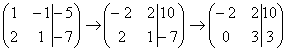. Теперь первую строку можно разделить «обратно» на –2: 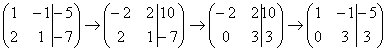. Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче:

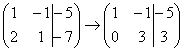
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »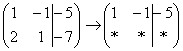

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 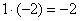, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

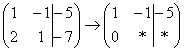«Теперь второй столбец. Вверху –1 умножаю на –2: 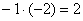. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

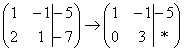«И третий столбец. Вверху –5 умножаю на –2: 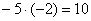. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

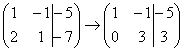Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе 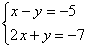. Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

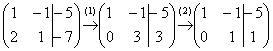
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: 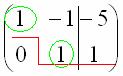. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

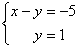
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат: .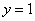

Рассмотрим первое уравнение системы 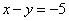и подставим в него уже известное значение «игрек»:

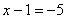
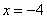
Ответ: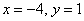

Прямая линия на плоскости.

Прямая –это геометрическое место точек, удовлетворяющих общему уравнению на плоскости :

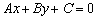Вектор, который параллелен прямой, называется направляющим вектором данной прямой. Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).

Направляющий вектор обозначают следующим образом: .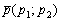

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку 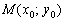, которая принадлежит прямой.Как составить уравнение прямой по точке и направляющему вектору?

Если известна некоторая точка 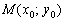, принадлежащая прямой, и направляющий вектор 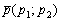этой прямой, то уравнение данной прямой можно составить по формуле:

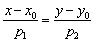
Уравнение прямой 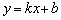называется уравнением прямой с угловым коэффициентом 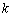. Например, если прямая задана уравнением 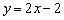, то её угловой коэффициент: 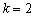. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

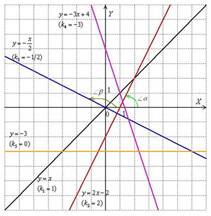
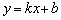
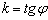
В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси и данной прямой: 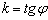, причём угол 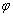«откручивается» против часовой стрелки.

угловой коэффициент характеризует степень наклона прямой к оси абсцисс.