Тригонометрические уравнения
Все формулы по алгебре и геометрии
Формулы сокр. умножения и разложения на множители :
(a± b)² =a² ± 2ab+b²
(a± b)³ =a³ ± 3a² b+3ab² ± b³
a² -b² =(a+b)(a-b)
a³ ± b³ =(a± b)(a² ∓ab+b² ),
(a+b)³ =a³ +b³ +3ab(a+b)
(a-b)³ =a³ -b³ -3ab(a-b)
xn-an=(x-a)(xn-1+axn-2+a² xn-3+...+an-1)
ax² +bx+c=a(x-x1)(x-x2)
где x1 и x2 — корни уравнения
ax² +bx+c=0
Степени и корни :
ap· ag = ap+g
ap:ag=a p-g
(ap)g=a pg
ap /bp = (a/b)p
ap× bp = abp
a0=1; a1=a
a-p = 1/a
pÖ a =b => bp=a
pÖ apÖ b = pÖ ab
Ö a ; a = 0
Квадратное уравнение
ax² +bx+c=0; (a¹ 0)
x1,2= (-b± Ö D)/2a; D=b² -4ac
D>0® x1¹ x2 ;D=0® x1=x2
D<0, корней нет.
Теорема Виета:
x1+x2 = -b/a
x1× x2 = c/a
Приведенное кв. Уравнение:
x² + px+q =0
x1+x2 = -p
x1× x2 = q
Если p=2k (p-четн.)
и x² +2kx+q=0, то x1,2 = -k± Ö (k² -q)
Нахождение длинны отр-ка по его координатам
Ö ((x2-x1)² -(y2-y1)² )
Логарифмы:
loga x = b => ab = x; a>0,a¹ 0
a loga x = x, logaa =1; loga 1 = 0
loga x = b; x = ab
loga b = 1/(log b a)
logaxy = logax + loga y
loga x/y = loga x - loga y
loga xk =k loga x (x >0)
logak x =1/k loga x
loga x = (logc x)/( logca); c>0,c¹ 1
logbx = (logax)/(logab)
Прогрессии
Арифметическая
an = a1 +d(n-1)
Sn = ((2a1+d(n-1))/2)n
Геометрическая
bn = bn-1 × q
b2n = bn-1× bn+1
bn = b1× qn-1
Sn = b1 (1- qn)/(1-q)
S= b1/(1-q)
Тригонометрия.
sin x = a/c
cos x = b/c
tg x = a/b=sinx/cos x
ctg x = b/a = cos x/sin x
sin (p -a ) = sin a
sin (p /2 -a ) = cos a
cos (p /2 -a ) = sin a
cos (a + 2p k) = cos a
sin (a + 2p k) = sin a
tg (a + p k) = tg a
ctg (a + p k) = ctg a
sin² a + cos² a =1
ctg a = cosa / sina , a ¹ p n, nÎ Z
tga × ctga = 1, a ¹ (p n)/2, nÎ Z
1+tg² a = 1/cos² a , a ¹ p (2n+1)/2
1+ ctg² a =1/sin² a , a ¹ p n
Формулы сложения:
sin(x+y) = sin x cos y + cos x sin y
sin (x-y) = sin x cos y - cos x sin y
cos (x+y) = cos x cos y - sin x sin y
cos (x-y) = cos x cos y + sin x sin y
tg(x+y) = (tg x + tg y)/ (1-tg x tg y )
x, y, x + y ¹ p /2 + p n
tg(x-y) = (tg x - tg y)/ (1+tg x tg y)
x, y, x - y ¹ p /2 + p n
Формулы двойного аргумента.
sin 2a = 2sin a cos a
cos 2a = cos² a - sin² a = 2 cos² a - 1 =
= 1-2 sin² a
tg 2a = (2 tga )/ (1-tg² a )
1+ cos a = 2 cos² a /2
1-cosa = 2 sin² a /2
tga = (2 tg (a /2))/(1-tg² (a /2))
Ф-лы половинного аргумента.
sin² a /2 = (1 - cos a )/2
cos² a /2 = (1 + cosa )/2
tg a /2 = sina /(1 + cosa ) = (1-cos a )/sin a
a ¹ p + 2p n, n Î Z
Ф-лы преобразования суммы в произв.
sin x + sin y = 2 sin ((x+y)/2) cos ((x-y)/2)
sin x - sin y = 2 cos ((x+y)/2) sin ((x-y)/2)
cos x + cos y = 2cos (x+y)/2 cos (x-y)/2
cos x - cos y = -2sin (x+y)/2 sin (x-y)/2
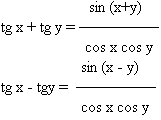
Формулы преобр. произв. в сумму
sin x sin y = ½ (cos (x-y) - cos (x+y))
cos x cos y = ½ (cos (x-y)+ cos (x+y))
sin x cos y = ½ (sin (x-y)+ sin (x+y))
Соотношение между функциями
sin x = (2 tg x/2)/(1+tg2x/2)
cos x = (1-tg2 2/x)/ (1+ tg² x/2)
sin2x = (2tgx)/(1+tg2x)
sin² a = 1/(1+ctg² a ) = tg² a /(1+tg² a )
cos² a = 1/(1+tg² a ) = ctg² a / (1+ctg² a )
ctg2a = (ctg² a -1)/ 2ctga
sin3a = 3sina -4sin³ a = 3cos² a sina -sin³ a
cos3a = 4cos³ a -3 cosa= cos³ a -3cosa sin² a
tg3a = (3tga -tg³ a )/(1-3tg² a )
ctg3a = (ctg³ a -3ctga )/(3ctg² a -1)
sin a /2 = ± Ö ((1-cosa )/2)
cos a /2 = ± Ö ((1+cosa )/2)
tga /2 = ± Ö ((1-cosa )/(1+cosa ))=
sina /(1+cosa )=(1-cosa )/sina
ctga /2 = ± Ö ((1+cosa )/(1-cosa ))=
sina /(1-cosa )= (1+cosa )/sina
sin(arcsin a ) = a
cos( arccos a ) = a
tg ( arctg a ) = a
ctg ( arcctg a ) = a
arcsin (sina ) = a ; a Î [-p /2 ; p /2]
arccos(cos a ) = a ; a Î [0 ; p ]
arctg (tg a ) = a ; a Î [-p /2 ; p /2]
arcctg (ctg a ) = a ; a Î [ 0 ; p ]
arcsin(sina )=
1)a - 2p k; a Î [-p /2 +2p k;p /2+2p k]
2) (2k+1)p - a ; a Î [p /2+2p k;3p /2+2p k]
arccos (cosa ) =
1) a -2p k ; a Î [2p k;(2k+1)p ]
2) 2p k-a ; a Î [(2k-1)p ; 2p k]
arctg(tga )= a -p k
a Î (-p /2 +p k;p /2+p k)
arcctg(ctga ) = a -p k
a Î (p k; (k+1)p )
arcsina = -arcsin (-a )= p /2-arccosa =
= arctg a /Ö (1-a ² )
arccosa = p -arccos(-a )=p /2-arcsin a =
= arc ctga /Ö (1-a ² )
arctga =-arctg(-a ) = p /2 -arcctga =
= arcsin a /Ö (1+a ² )
arc ctg a = p -arc cctg(-a ) =
= arc cos a /Ö (1-a ² )
arctg a = arc ctg1/a =
= arcsin a /Ö (1+a ² )= arccos1/Ö (1+a ² )
arcsin a + arccos = p /2
arcctg a + arctga = p /2
Тригонометрические уравнения
sin x = m ; |m| = 1
x = (-1)n arcsin m + p k, kÎ Z
sin x =1 sin x = 0
x = p /2 + 2p k x = p k
sin x = -1
x = -p /2 + 2 p k
cos x = m; |m| = 1
x = ± arccos m + 2p k
cos x = 1 cos x = 0
x = 2p k x = p /2+p k
cos x = -1
x = p + 2p k
tg x = m
x = arctg m + p k
ctg x = m
x = arcctg m +p k
sin x/2 = 2t/(1+t2); t - tg
cos x/2 = (1-t² )/(1+t² )
Показательные уравнения.
Неравенства: Если af(x)>(<) aа(ч)
1) a>1, то знак не меняеться.
2) a<1, то знак меняется.
Логарифмы : неравенства:
logaf(x) >(<) log a j (x)
1. a>1, то : f(x) >0
j (x)>0
f(x)>j (x)
2. 0<a<1, то: f(x) >0
j (x)>0
f(x)<j (x)
3. log f(x) j (x) = a
ОДЗ: j (x) > 0
f(x) >0
f(x ) ¹ 1
Тригонометрия:
1. Разложение на множители:
sin 2x - Ö 3 cos x = 0
2sin x cos x -Ö 3 cos x = 0
cos x(2 sin x - Ö 3) = 0
....
2. Решения заменой ....
3.sin² x - sin 2x + 3 cos² x =2
sin² x - 2 sin x cos x + 3 cos ² x = 2 sin² x + cos² x
Дальше пишеться если sin x = 0, то и cos x = 0,
а такое невозможно, => можно поделить на cos x
Тригонометрические нер-ва :
Sin a ³ m
2p k+a 1 = a = a 2+ 2p k
2p k+a 2 = a = (a 1+2p )+ 2p k
Пример:
I cos (p /8+x) < Ö 3/2
p k+ 5p /6< p /8 +x< 7p /6 + 2p k
2p k+ 17p /24 < x< p /24+2p k;;;;
II sin a = 1/2
2p k +5p /6 = a = 13p /6 + 2p k
cos a ³ (= ) m
2p k + a 1 < a < a 2+2 p k
2p k+a 2< a < (a 1+2p ) + 2p k
cos a ³ - Ö 2/2
2p k+5p /4 = a = 11p /4 +2p k
tg a ³ (= ) m
p k+ arctg m = a = arctg m + p k
ctg ³ (= ) m
p k+arcctg m < a < p +p k
Производная:
(xn)’ = n× xn-1
(ax)’ = ax× ln a
(lg ax )’= 1/(x× ln a)
(sin x)’ = cos x
(cos x)’ = -sin x
(tg x)’ = 1/cos² x
(ctg x)’ = - 1/sin² x
(arcsin x)’ = 1/ Ö (1-x² )
(arccos x)’ = - 1/ Ö (1-x² )
(arctg x)’ = 1/ Ö (1+x² )
(arcctg x)’ = - 1/ Ö (1+x² )
Св-ва:
(u × v)’ = u’× v + u× v’
(u/v)’ = (u’v - uv’)/ v²
Уравнение касательной к граф.
y = f(x0)+ f ’(x0)(x-x0)
уравнение к касательной к графику в точке x
1. Найти производную
2. Угловой коофициент k = производная в данной точке x
3. Подставим X0, f(x0), f ‘ (x0), выразим х
Интегралы :
ò xn dx = xn+1/(n+1) + c
ò ax dx = ax/ln a + c
ò ex dx = ex + c
ò cos x dx = sin x + cos
ò sin x dx = - cos x + c
ò 1/x dx = ln|x| + c
ò 1/cos² x = tg x + c
ò 1/sin² x = - ctg x + c
ò 1/Ö (1-x² ) dx = arcsin x +c
ò 1/Ö (1-x² ) dx = - arccos x +c
ò 1/1+ x² dx = arctg x + c
ò 1/1+ x² dx = - arcctg x + c
