Метод интервалов для непрерывных функций
1. Все члены неравенства переносим в левую часть;
2. Выражение, стоящее в левой части, принимаем как 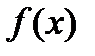 ;
;
3. Находим область определения функции;
4. Находим нули функции и отмечаем их на области определения;
5. Расставляем знаки функции на полученных промежутках;
6. В зависимости от знака исходного неравенства записываем ответ.
При решении рациональных неравенств вида 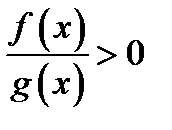
(знак неравенства может быть любым) можно использовать упрощённый алгоритм:
1. Находим «нули» числителя;
2. Находим «нули» знаменателя;
3. Полученные точки расставляем на числовой прямой;
4. Определяем знаки левой части неравенства на полученных промежутках;
5. По знаку исходного неравенства выбираем нужные промежутки и записываем ответ.
При расстановке знаков начинаем с крайнего правого промежутка, знак на нём определяем либо непосредственной подстановкой какого-либо числа, либо по знаку старшего члена числителя и знаменателя. Учитываем, что знаки функции на промежутках чередуются не всегда. Это зависит от кратности корней, которые получаются в процессе решения неравенства. Если кратность корня чётная, то слева и справа от него знаки одинаковые. Если -нечётная, то слева и справа - различные знаки.
Формулы сокращённого умножения.
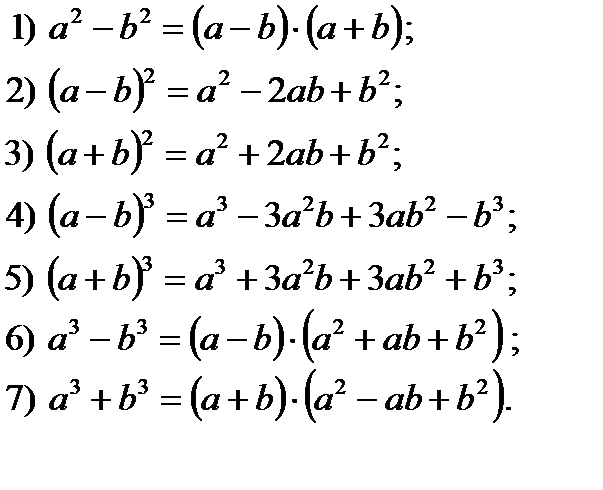 Формулы, не изменяющие аргумент.
Формулы, не изменяющие аргумент. 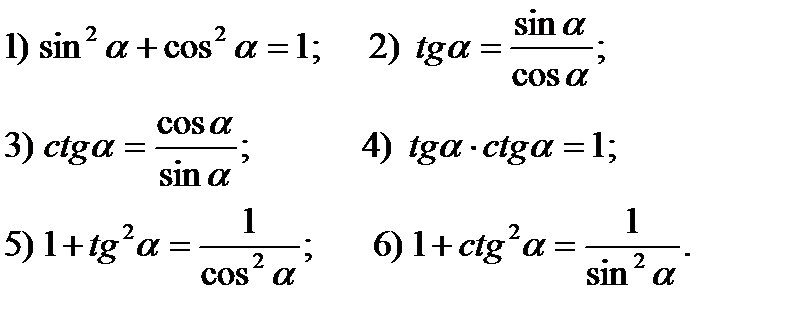 Некоторые формулы приведения.
Некоторые формулы приведения. 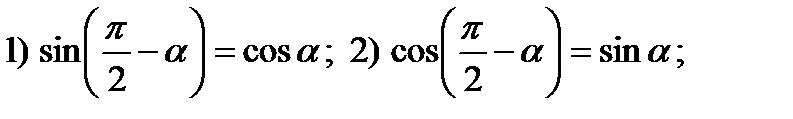 Формулы сложения аргументов.
Формулы сложения аргументов.
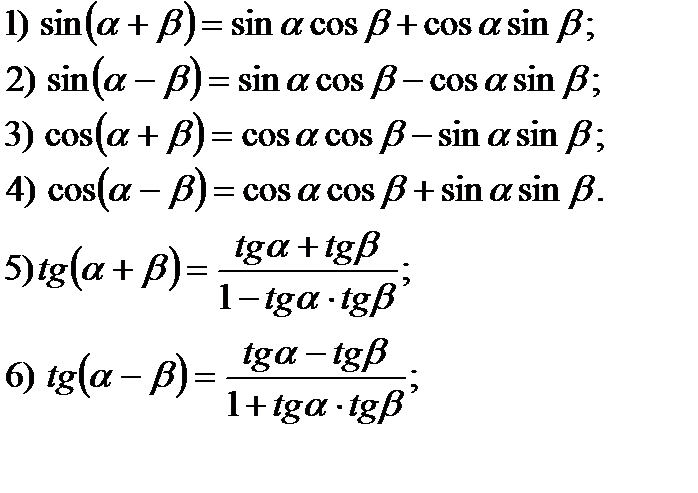 Формулы двойного аргумента.
Формулы двойного аргумента.
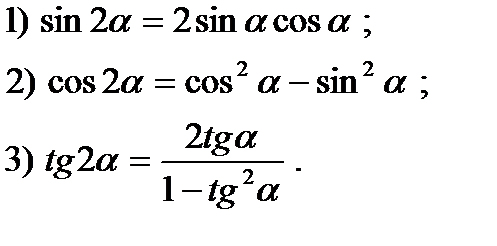
Формулы понижения степени.
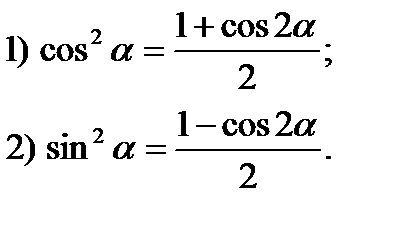
Формулы сложения тригонометрических функций. 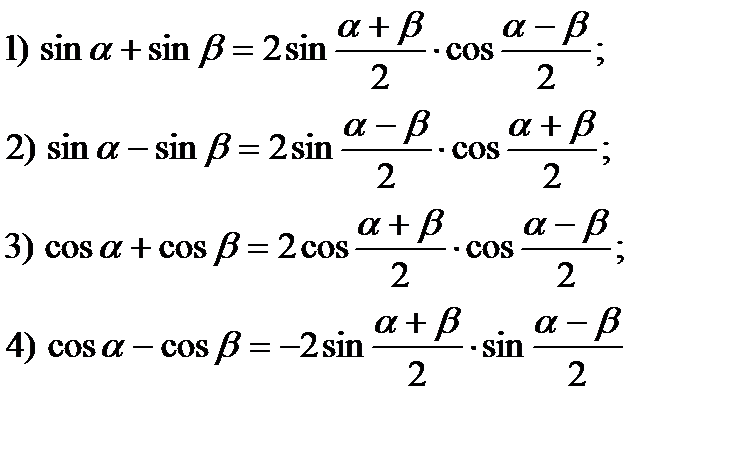
Формулы преобразования произведений тригонометрических функций в суммы.
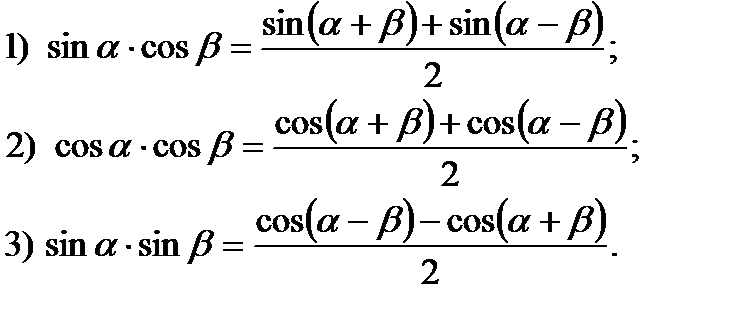
Формулы введения вспомогательного
аргумента.
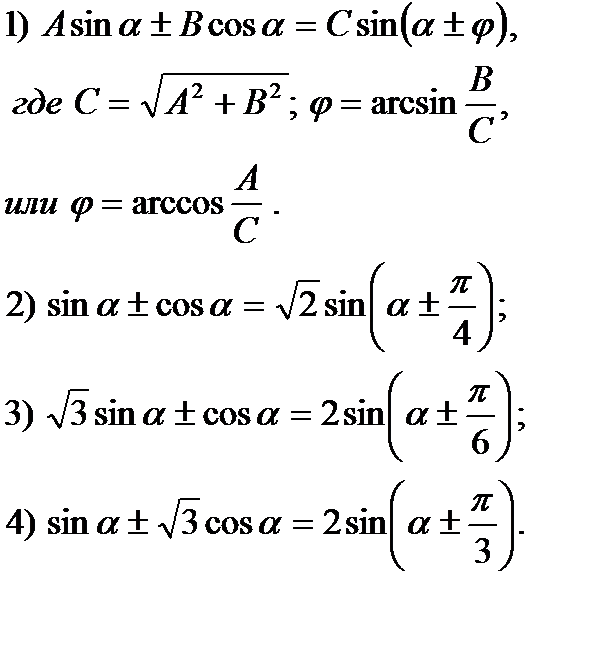
Универсальная подстановка.
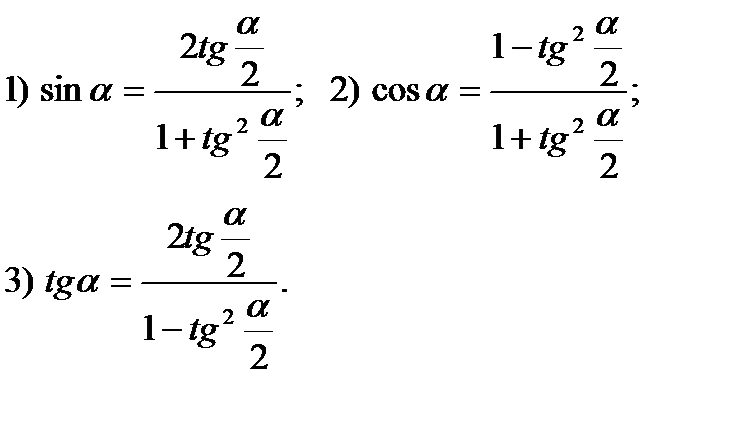
1. Определение. 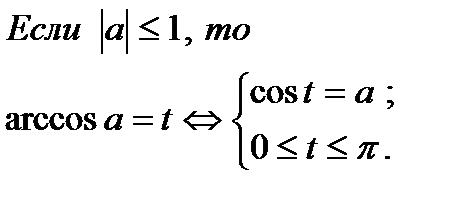 Для любого Для любого 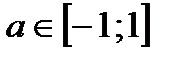 выполняется равенство выполняется равенство 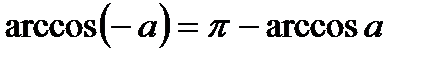 . Если . Если 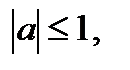 то уравнение то уравнение 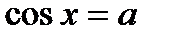 имеет решения: имеет решения: 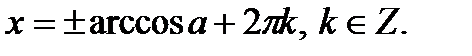 Частные случаи: Частные случаи: 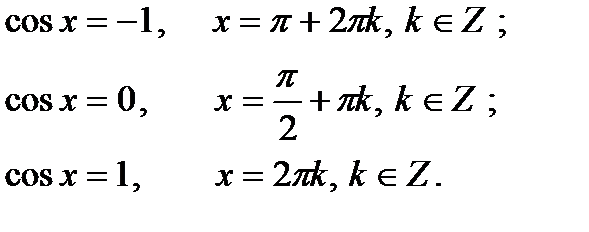 Если Если 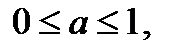 то уравнение то уравнение 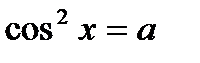 имеет решения: имеет решения: 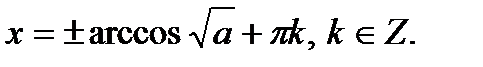 |
3. Определение. 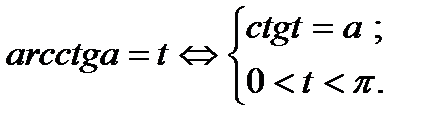 Для любого Для любого 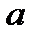 выполняется равенство выполняется равенство 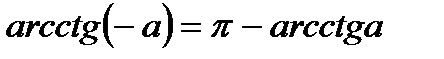 . Для любого . Для любого 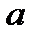 уравнение уравнение 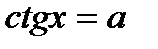 имеет решения: имеет решения: 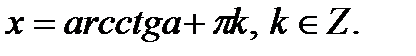 Частные случаи: Частные случаи: 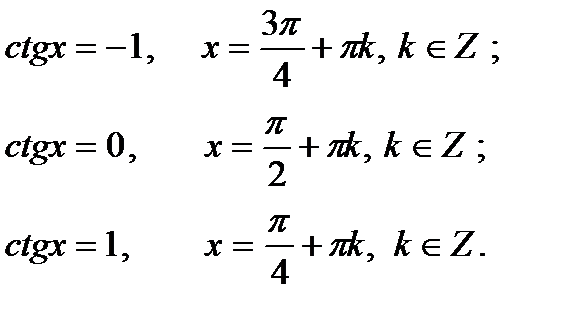 Если Если 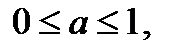 то уравнение то уравнение 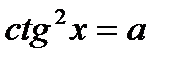 имеет решения: имеет решения: 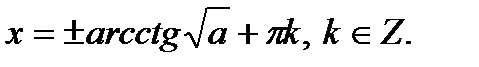 |
2. Определение. 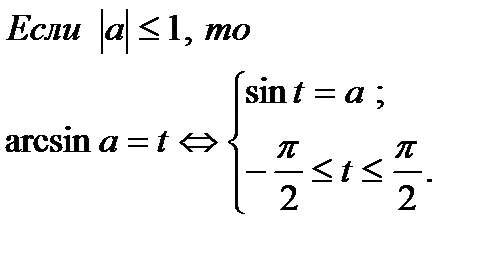 Для любого Для любого 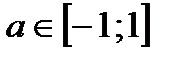 выполняется равенство выполняется равенство 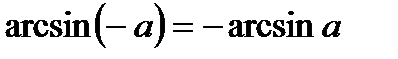 . Если . Если 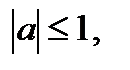 то уравнение то уравнение 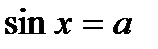 имеет решения: имеет решения: 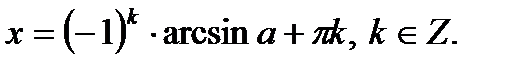 Решения этого уравнения можно записать по-другому: Решения этого уравнения можно записать по-другому: 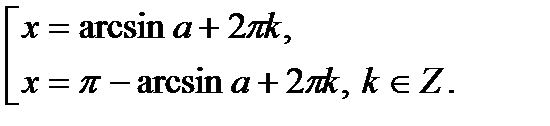 Частные случаи: Частные случаи: 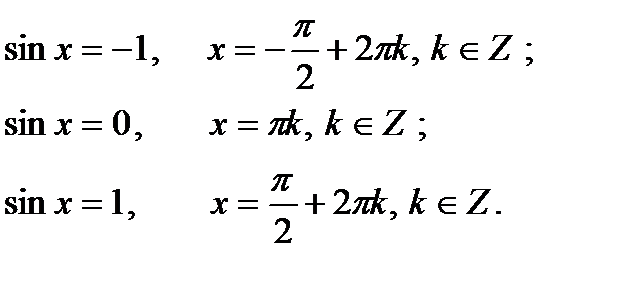 Если Если 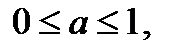 то уравнение то уравнение 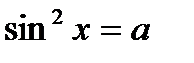 имеет решения: имеет решения: 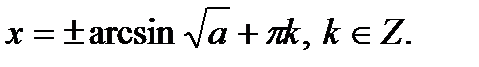 |
4. Определение. 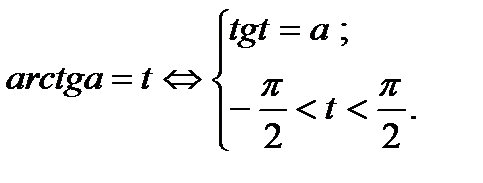 Для любого Для любого 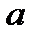 выполняется равенство выполняется равенство 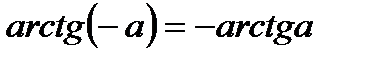 . Для любого . Для любого 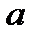 уравнение уравнение 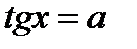 имеет решения: имеет решения: 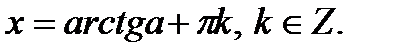 Частные случаи: Частные случаи: 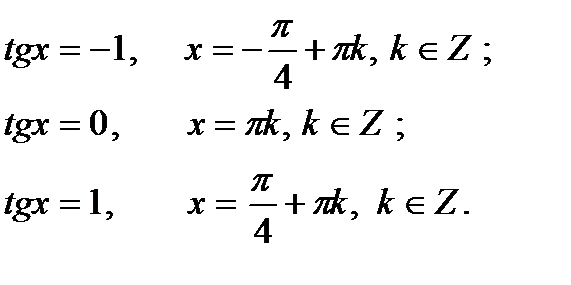 Если Если 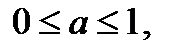 то уравнение то уравнение 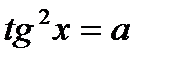 имеет решения: имеет решения: 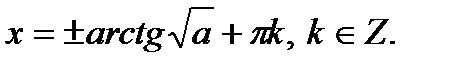 |
Формулы производных для некоторых функций. 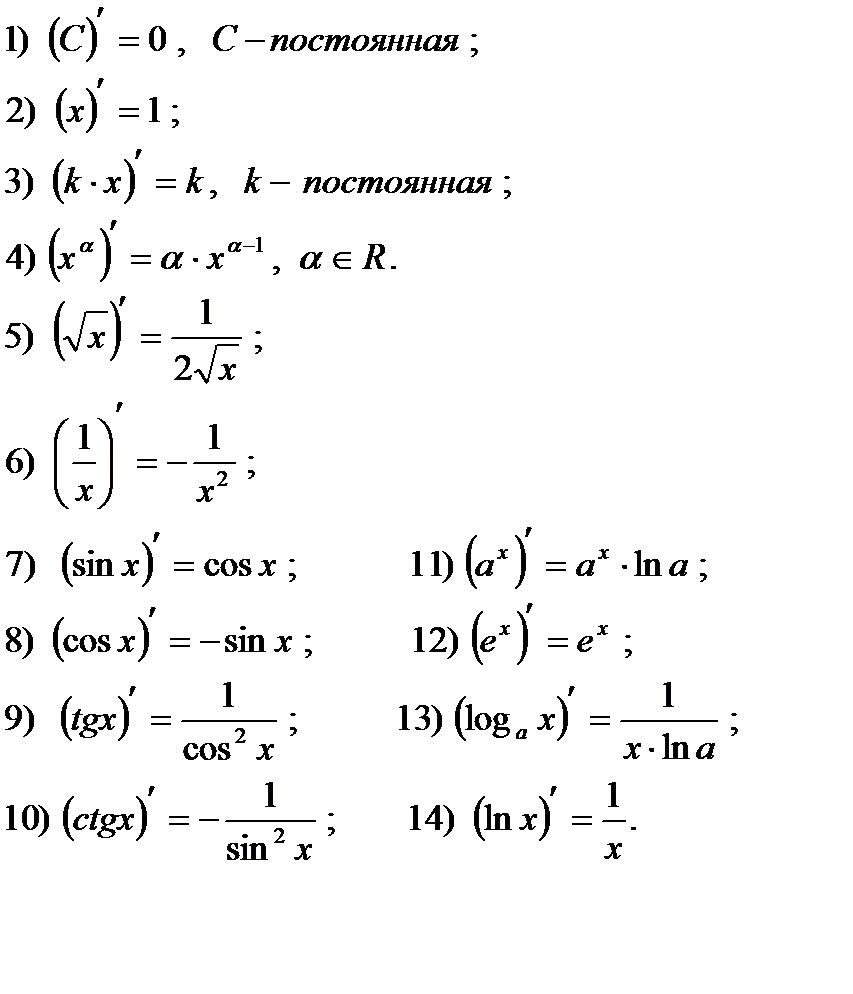 | Правила дифференцирования. 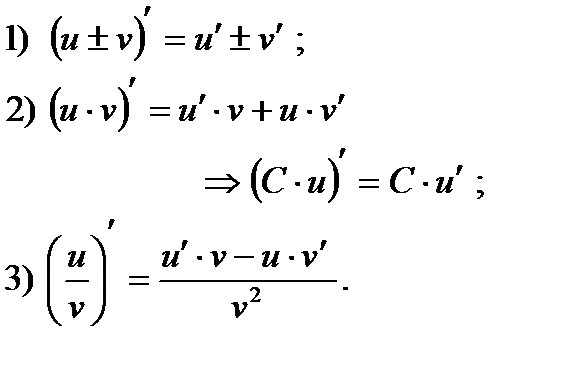 Дифференцирование сложной функции. Дифференцирование сложной функции. 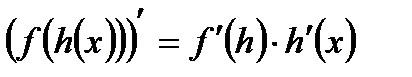 . Уравнение касательной. . Уравнение касательной. 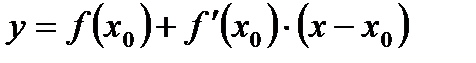 . . |
Таблица первообразных для некоторых функций.
Функция 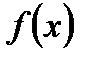 | 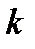 (постоянная) (постоянная) |  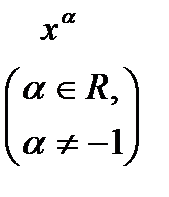 | 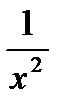 | 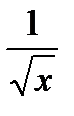 | 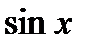 | 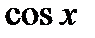 |
Общий вид первообразных 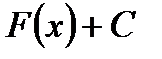 | 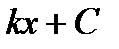 | 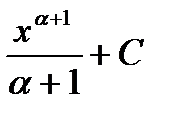 | 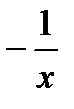 +С +С | 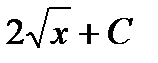 | 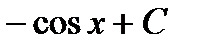 | 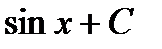 |
Функция 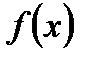 | 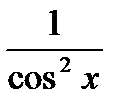 | 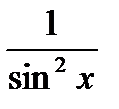 | 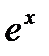 | 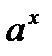 | 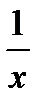 | ||
Общий вид первообразных 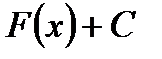 | 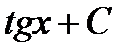 | 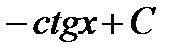 | 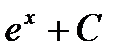 | 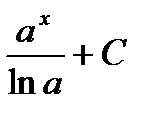 | 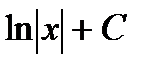 | ||
Формула Ньютона-Лейбница: 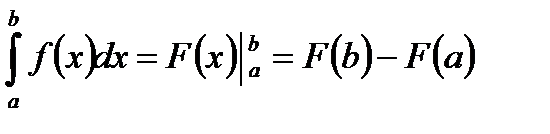 . . | Три правила нахождения первообразных: 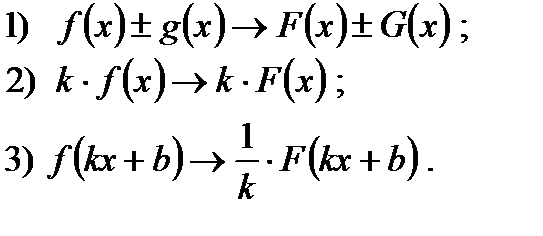 | ||||||
