Задачи для самостоятельного решения.
1.3.1.Даны числа 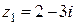 ,
, 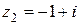 ,
, 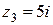 . Найдите:
. Найдите:
а) 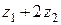 , б)
, б) 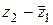 ; в)
; в) 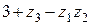 ; г)
; г) 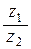 ; д)
; д) 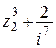 .
.
Заданные числа и результаты вычислений изобразите на комплексной плоскости.
1.3.2.Комплексные числа 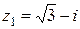 ,
, 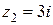 ,
, 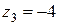 ,
, 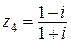 запишите в тригонометрической и показательной формах. Изобразите эти числа на комплексной плоскости.
запишите в тригонометрической и показательной формах. Изобразите эти числа на комплексной плоскости.
1.3.3.Вычислите:
а) 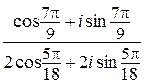 ; б)
; б) 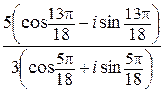 ;
;
в) 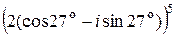 ; г)
; г)  ;
;
д) 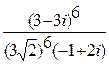 ; е)
; е) 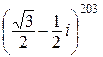 .
.
Результат представьте в алгебраической форме.
1.3.4.Найдите все значения корней: а) 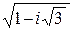 , б)
, б) 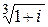 .
.
1.3.5.Найдите:
а) 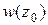 , если
, если 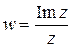 ,
, 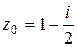 ;
;
б) 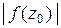 , если
, если 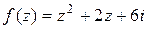 , а
, а 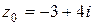 ;
;
в) f(1+2i), если 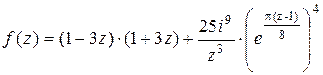 .
.
1.3.6.Решите уравнения:
а) 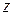 2–4z +5 = 0; б)
2–4z +5 = 0; б) 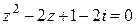 ; в)
; в) 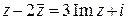 .
.
1.3.7.Решите систему уравнений 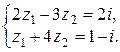
1.3.8.Укажите на плоскости множество точек, удовлетворяющих условию:
а) ½z½> 2 – Re z; б) 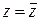 ; в) ½z – 2i½=½z + 3½.
; в) ½z – 2i½=½z + 3½.
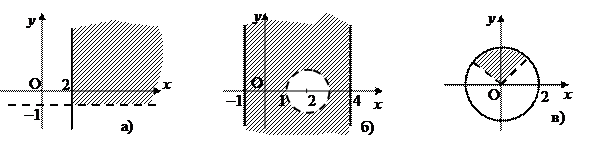 |
1.3.11. Опишите с помощью неравенств множества точек комплексной плоскости, изображенные на рисунках:
1.3.12. Постройте область 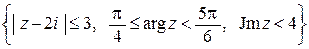 .
.
Тест для самоконтроля
по теме «Комплексные числа»
1. Комплексное число 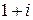 в тригонометрической форме имеет вид:
в тригонометрической форме имеет вид:
а) 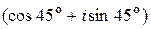 ; б)
; б) 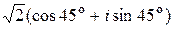 ;
;
в) 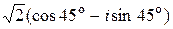 ; г)
; г) 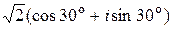 .
.
2. Частное 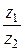 комплексных чисел
комплексных чисел 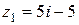 и
и 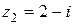 равно
равно
а) 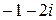 ; б)
; б) 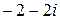 ; в)
; в) 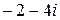 ; г)
; г) 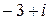 .
.
3. Корнем уравнения 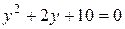 является число
является число
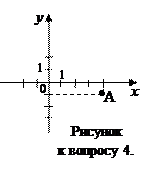 а)
а) 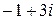 ; б)
; б) 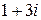 ; в) 2; г) 4.
; в) 2; г) 4.
4. Данному изображению точки А (рисунок справа) соответствует комплексное число:
а) 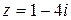 ; б)
; б) 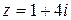 ;
;
в) 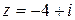 ; г)
; г) 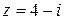 .
.
5. Корнями из комплексного числа 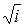 являются
являются
а) 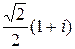 ; б)
; б) 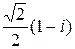 ; в)
; в) 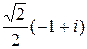 ; г)
; г) 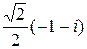 .
.
6. Корнями уравнения 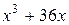 на множестве комплексных чисел являются числа:
на множестве комплексных чисел являются числа:
а) 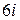 ; б) 6; в) 0; г)
; б) 6; в) 0; г) 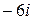 ; д) –6.
; д) –6.
7. Для каждого многочлена 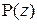 (список 1-3) укажите его значение в точке
(список 1-3) укажите его значение в точке 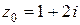 (список (а-д):
(список (а-д):
1) 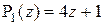 ; 2)
; 2) 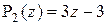 ; 3)
; 3) 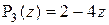 .
.
а) 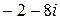 ; б)
; б) 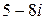 ; в)
; в) 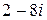 ; г)
; г) 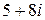 д)
д) 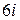 .
.
8. Если 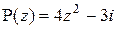 , то значение производной этого многочлена в точке
, то значение производной этого многочлена в точке 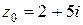 равно:
равно:
а) 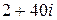 ; б)
; б) 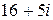 ; в)
; в) 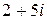 ; г)
; г) 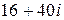 .
.
9. Если 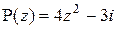 и
и 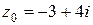 ,
, 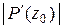 равно:
равно:
а) 5; б) 20; в) 40; г) 100.
10. Если 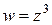 , то мнимая и действительная части
, то мнимая и действительная части 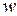 равны:
равны:
а) 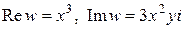 ;
;
б) 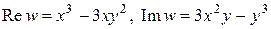 ;
;
в) 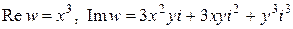 ;
;
г) 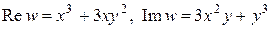 .
.
11. Если 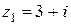 , а
, а 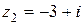 , то модуль произведения
, то модуль произведения 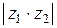 равен:
равен:
а) 1; б) 4 ; в) 10; г) 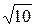 .
.
12. Установите соответствие между комплексными числами 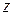 (список 1 - 3) и их аргументами
(список 1 - 3) и их аргументами 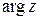 (список а - д):
(список а - д):
1) 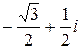 ; 2)
; 2) 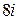 ; 3)
; 3) 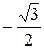 ;
;
а) 0; б) 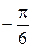 ; в)
; в) 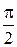 ; г)
; г) 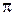 ; д)
; д) 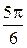 .
.
Если вы смогли:
- ответить на большинство вопросов для самопроверки;
- справиться с решением перечисленных выше задач для самостоятельного решения;
- решить задачи 1– 4 индивидуального задания №1;
- ответить на большую часть вопросов теста для самоконтроля,
то можете считать, что тему «Комплексные числа» вы усвоили, но только лишь на оценку «хорошо».
Если же вы хотите получить более высокую оценку, и уверены в своих силах, работу над темой необходимо продолжить: ниже приведены вопросы и задачи второго уровня сложности, попробуйте ответить на них. В случае успеха вы можете с уверенностью рассчитывать на высокую оценку и на защите темы, и на предстоящем в конце семестра экзамене.
Затем можно переходить к изучению темы «Многочлены».
1.4 Контрольные вопросы
1) Может ли сумма квадратов двух комплексных чисел быть отрицательной? Если да, то приведите пример.
2) Найдите все числа, сопряженные своему квадрату.
3) При каких условиях модуль суммы двух комплексных чисел равен разности модулей слагаемых?
4) При каких условиях модуль суммы двух комплексных чисел равен сумме модулей слагаемых?
5) Докажите, что 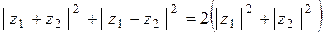 . Каков геометрический смысл этого неравенства?
. Каков геометрический смысл этого неравенства?
6) Докажите, что 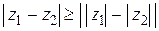 . Каков геометрический смысл этого неравенства?
. Каков геометрический смысл этого неравенства?
7) Докажите, что если в результате применения конечного числа операций сложения, вычитания, умножения и деления над числами 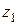 и
и 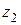 получится число
получится число 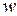 , то в результате применения тех же операций над сопряженными числами
, то в результате применения тех же операций над сопряженными числами 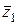 и
и 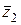 получится число
получится число 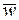 , сопряженное с
, сопряженное с 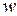 .
.
8) Докажите, что модуль произведения двух комплексных чисел равен произведению модулей этих чисел.
9) Используя формулу Муавра, выразите функцию cos4j через cosj и sinj.
10) Представьте в тригонометрической форме комплексные числа:
а) 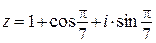 ; б)
; б) 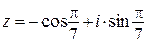 ;
;
11) Запишите в показательной форме числа:
а) 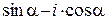 ; б)
; б) 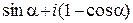 .
.
12) Докажите формулы Эйлера 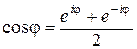 ,
, 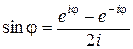 .
.
13) Докажите равенства:
а) 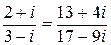 ; б)
; б) 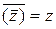 ; в)
; в) 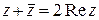 ; г)
; г) 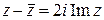 .
.
14) Дайте геометрическое описание множества всех точек удовлетворяющих условию:
а) 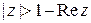 ; б)
; б) 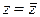 ; в)
; в) 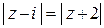 ; г)
; г) 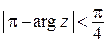 .
.
*) Выбор границ изменения главного значения аргумента: или , зависит от конкретных условий решаемой задачи. Чаще всего, значение выбирают исходя, например, из простоты записи результата или удобства дальнейших вычислений.
*) При записи комплексного числа в тригонометрической форме , как правило, используют главное значение аргумента: .
**) Значение α можно вычислить с помощью калькулятора или используя таблицы Брадиса значений тригонометрических функции, а в некоторых случаях значение угла α так и оставляют в виде .
