Признак Даламбера сходимости рядов с положительными членами

Теорема 3 (признак Даламбера). Пусть дан ряд с положительными членами 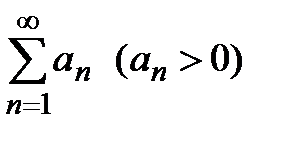, и существует конечный предел 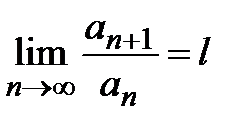, тогда:
1) ряд 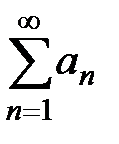сходится, если ,
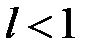2) ряд 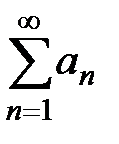расходится, если ,
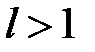3) если 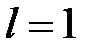, то для выяснения сходимости ряда признак Даламбера не применим.

Доказательство. 1) Пусть предел 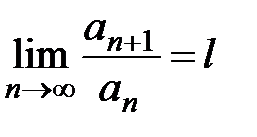существует и 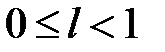. Рассмотрим число q такое, что 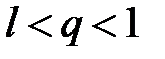. Из определения предела следует, что 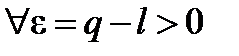существует 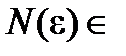N, начиная с которого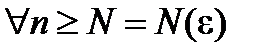
выполняется неравенство 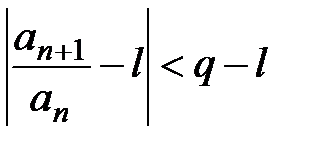, 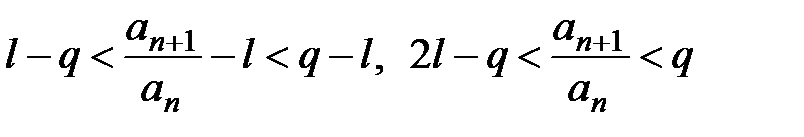. Таким образом,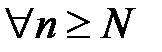 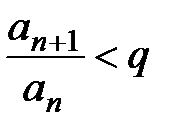, т.е. 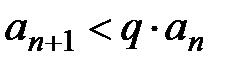. Берём n = N, N+1, N+2,…, тогда , , , …, .

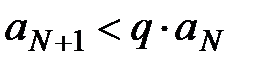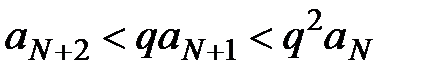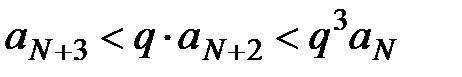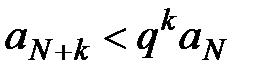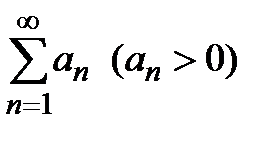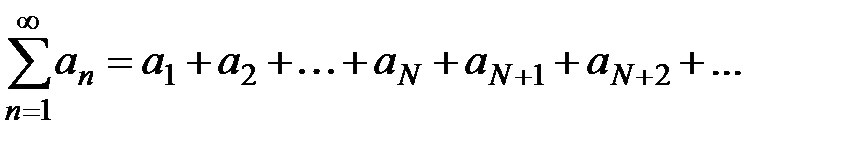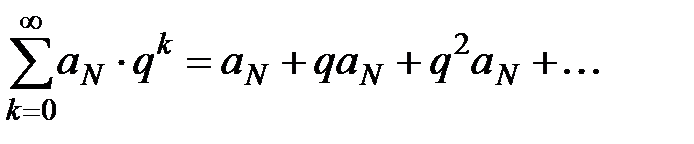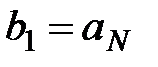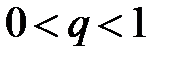Запишем исходный ряд в виде: . Рассмотрим новый ряд . Этот ряд есть ряд геометрической прогрессии с и , который сходится, а значит, сходится ряд 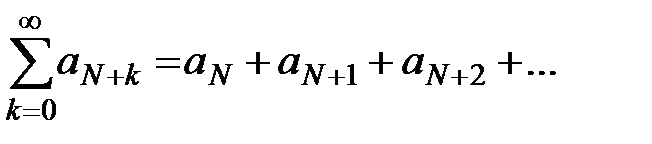, так как 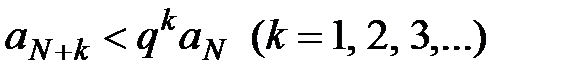на основании теоремы 1. Ряд 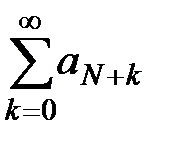получен из исходного 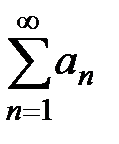отбрасыванием конечного числа членов 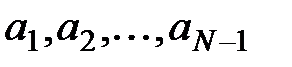, тогда ряд 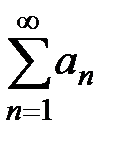сходится (свойство 1, лекция 1, разд. 1.3). Таким образом, исходный ряд 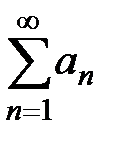сходится, если 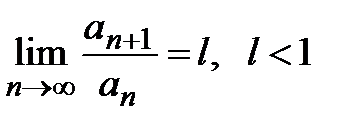. Первая часть теоремы доказана.

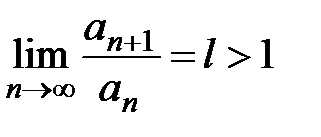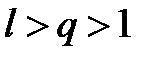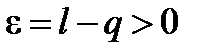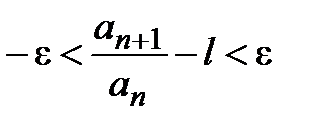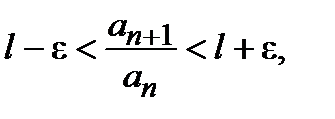
2) Пусть . Рассмотрим число q такое, что . , из определения предела следует: , 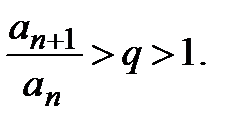Таким образом, 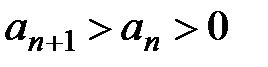и при 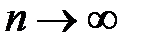общий член ряда 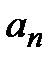не стремится к 0, т.е. ряд 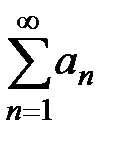расходится, так как не выполняется необходимое условие сходимости ряда (теорема 1, лекция 1, разд. 1.3). Вторая часть теоремы доказана.

3) Если 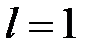, 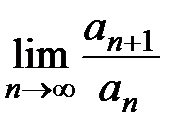равен единице или не существует, в этом

случае для выяснения сходимости ряда признак Даламбера не применим.

Пример 6. Исследовать на сходимость ряд .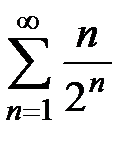

Решение. Обозначим 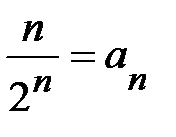, 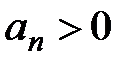; найдём 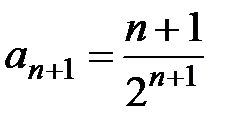. Составим предел 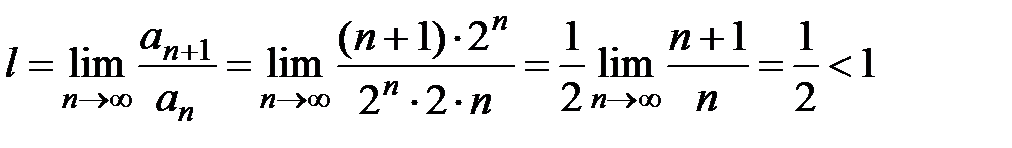, т.е. по признаку Даламбера ряд сходится.

Ответ: ряд 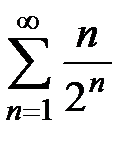сходится.

Пример 7. Исследовать на сходимость ряд .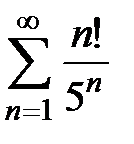

Решение. Обозначим 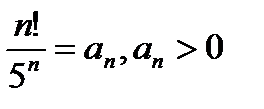; найдём 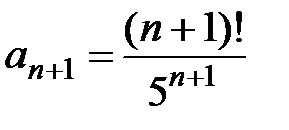. Составим предел

,

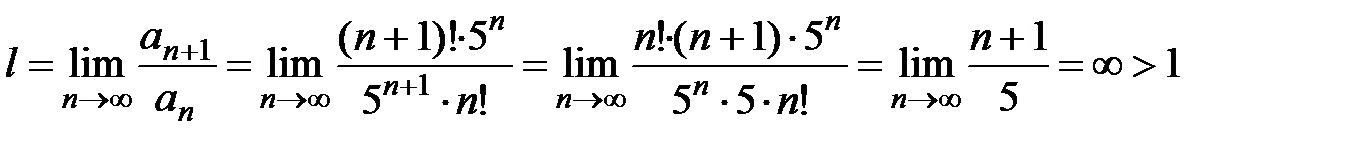т.е. по признаку Даламбера ряд расходится.

Ответ: ряд 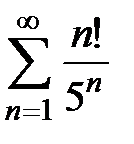расходится.

2.4. Радикальный признак Коши сходимости рядов
с положительными членами

Теорема 4 (радикальный признак Коши). Пусть дан ряд с положительными членами 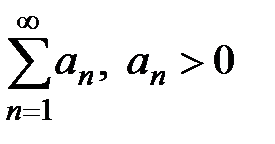и пусть существует конечный предел 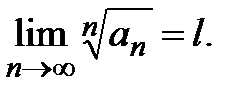Тогда:
1) если 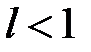, ряд сходится,
2) если 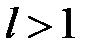, ряд расходится,
3) если 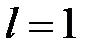, то для выяснения сходимости ряда радикальный признак Коши не применим.

Доказательство. 1) Пусть существует 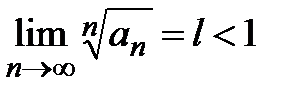; так как 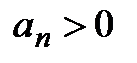, то 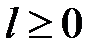. Рассмотрим число q такое, что 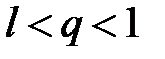. Из определения предела следует, что 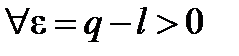существует 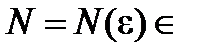N, начиная с которого 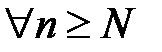выполняется неравенство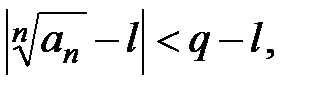 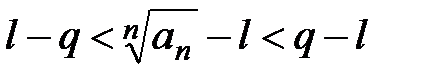, , 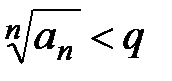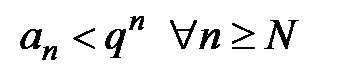. Распишем исходный ряд

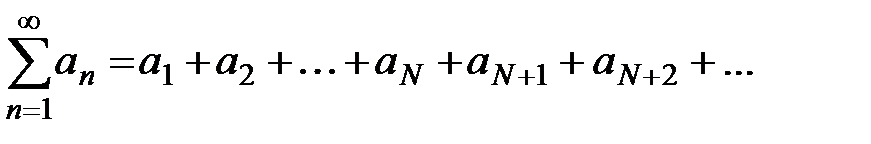. (1)
Составим новый ряд

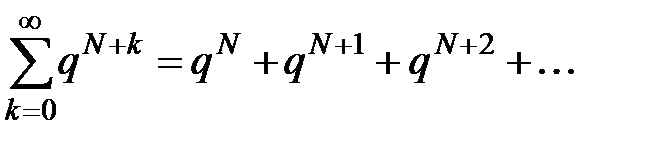. (2)

Ряд (2) представляет собой ряд геометрической прогрессии со знаменателем 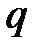: 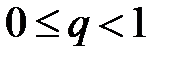, т.е. этот ряд сходится, а значит, ряд (1) сходится по I признаку сравнения рядов (теорема 1 данной лекции).

2) Пусть существует 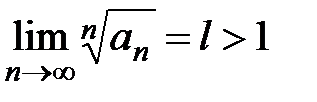. Начиная с некоторого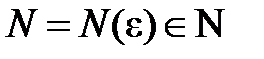 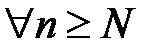, , 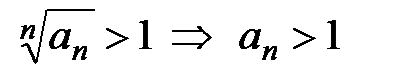т.е. 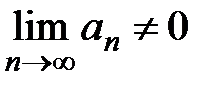, тогда исходный ряд расходится по необходимому признаку сходимости (теорема 1, лекция 1, разд. 1.3).
3) Если 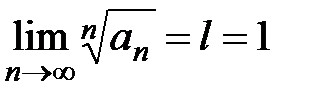(или не существует), то для выяснения сходимости ряда радикальный признак Коши не применим. Теорема доказана.

Пример 8. Исследовать на сходимость ряд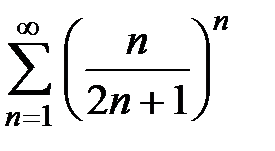

Решение. Обозначим 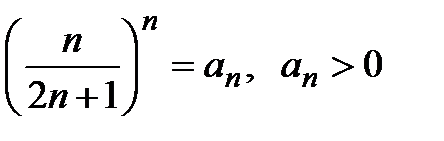. Составим предел:

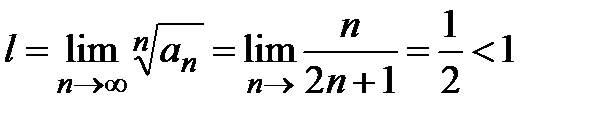, т.е. по радикальному признаку Коши ряд сходится.

Ответ: ряд 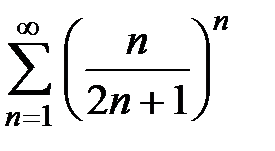сходится.