Охлаждение (нагревание) неограниченной пластины
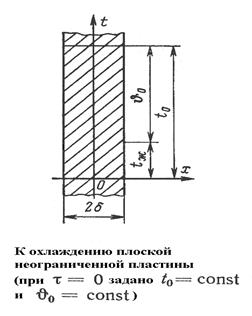
Дана пластина толщиной 2 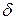 . Коэффициент теплоотдачи для всей поверхности пластины постоянен. Изменение температуры происходит только в одном направлении координаты х, т.е.
. Коэффициент теплоотдачи для всей поверхности пластины постоянен. Изменение температуры происходит только в одном направлении координаты х, т.е.  , а следовательно, задача является одномерной. Начальное распределение температуры задано некоторой функцией t(x,0)=f(x). Охлаждение происходит в среде с постоянной температурой tж=const. Отсчет избыточной температуры пластины для любого момента времени будем вести от температуры окружающей среды
, а следовательно, задача является одномерной. Начальное распределение температуры задано некоторой функцией t(x,0)=f(x). Охлаждение происходит в среде с постоянной температурой tж=const. Отсчет избыточной температуры пластины для любого момента времени будем вести от температуры окружающей среды 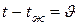 .
.
Дифференциальное уравнение теплопроводности
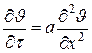 .
.
Начальные условия:
при 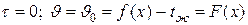 .
.
При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины.
Тогда граничные условия запишутся:
на оси пластины при х=0 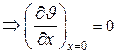 ;
;
на поверхности пластины при х= 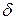
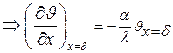 .
.
После решения дифференциального уравнения получаем, что безразмерная температура является функцией только двух безразмерных параметров:
для оси пластины 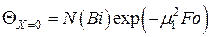 ;
;
для поверхности пластины 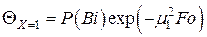 ,
,
где 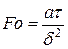 - число Фурье, представляющее собой безразмерное время,
- число Фурье, представляющее собой безразмерное время,
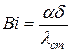 - число (критерий) Био.
- число (критерий) Био.
Критерий Био представляет собой отношение внутреннего термического сопротивления процесса теплопроводности к внешнему термическому сопротивлению процесса теплоотдачи.
Число Био называют критерием массивности. В зависимости от числа Ві тела подразделяются на термически тонкие (Bi<0,1) и термически массивные (Bi>100). Характер распределения температуры в теле можно определить в зависимости от численного значения числа Био. Рассмотрим три случая.
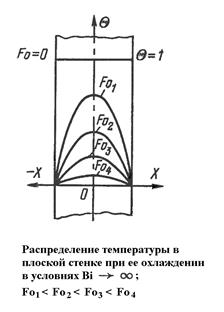
1. Bi→∞ (практически Bi>100). Если Bi→∞, то температура поверхности пластины сразу становится равной температуре окружающей среды, в которую помещена пластина. Точка пересечения касательных к температурным кривым находится на поверхности пластины.
Из 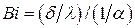 следует: Bi→∞ при заданных физических параметрах и толщине пластины тогда, когда
следует: Bi→∞ при заданных физических параметрах и толщине пластины тогда, когда 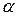 →∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела (внутренняя задача).
→∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела (внутренняя задача).
2. Bi→0 (практически Bi<0,1). Из 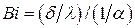 видно, что Bi→0 при малых размерах толщины пластины, большом значении коэффициента теплопроводности
видно, что Bi→0 при малых размерах толщины пластины, большом значении коэффициента теплопроводности 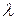 и малых значениях коэффициента теплоотдачи
и малых значениях коэффициента теплоотдачи 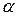 .
.
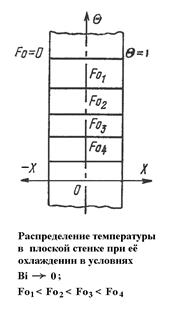
При малых Bi температура на поверхности пластины незначительно отличается от температуры его оси, т.е. температура по толщине пластины распределяется равномерно.
В этом случае процесс нагрева и охлаждения тела определяется интенсивностью теплоотдачи на поверхности пластины. Т.е. пути повышения интенсивности охлаждения следует искать во внешних условиях (внешняя задача).
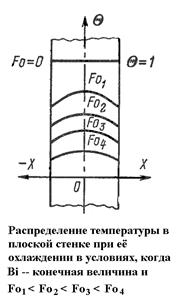
3. Число Ві находится в пределах 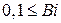 <100. Температурные кривые для любого момента времени будут выглядеть, как показано на рис. В этом случае интенсивность процесса охлаждения (нагревания) определяется как внутренним, так и внешним термическим сопротивлением.
<100. Температурные кривые для любого момента времени будут выглядеть, как показано на рис. В этом случае интенсивность процесса охлаждения (нагревания) определяется как внутренним, так и внешним термическим сопротивлением.
