Задания для самостоятельного решения. Даны множества и два бинарных отношения: и

Задание №1

Даны множества 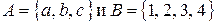и два бинарных отношения: 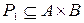и . И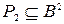зобразите Р₁, Р₂ графически. Найдите Р₁^-1, Р₂^-1, 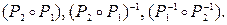Определите, является ли отношение Р₂ рефлексивным, транзитивным, симметричным, антисимметричным.

Задание №2

Найдите область определения и область значений отношения Р.Является ли отношение Р рефлексивным, транзитивным, симметричным, антисимметричным? Является ли оно отношением эквивалентности или упорядоченности?

Варианты заданий:

Вариант №1

1. Р₁ = {(а, 2); (а, 3); (а, 4); (b, 3); (с, 1); (с, 4)}

Р₂ = {(1, 1); (2, 3); (2, 2); (3, 4); (1, 4); (2, 4); (4, 2)}

2. P Í ℝ ² и Р = {(x, y) : x · y > 1, где x, y Î ℝ – вещественные числа }

3. P Í ℝ ² и Р = {(x, y) : 3x- y < -1, где x, y Î ℝ – вещественные числа }

Вариант №2

1. Р₁ = {(b, 2); (а, 3); (b, 1); (b, 4); (с, 1); (с, 2); (с, 4)}

Р₂ = {(1, 1); (1, 2); (1, 4); (2, 2); (2, 4); (3, 3); (3, 2); (3, 4); (4, 4)}

2. РÍ ℝ² и Р = {(x, y) : x²+ y²=1, где x, y Îℝ– вещественные числа }

3. РÍ ℝ² и Р = {(x, y) : -2xy =1, где x, y Îℝ– вещественные числа }

Вариант №3

1. Р₁ = {(а, 3); (а, 2); (а, 4); (b 1); (с, 2); (с, 4); (с, 3)}

Р₂ = {(1, 1); (2, 2); (2, 1); (3, 3); (4, 4); (4, 3); (1, 4); (2, 4); (3, 2); (3, 4)}

2 P Í ℝ² и Р = {(x, y) : y =|x|, где x, y Îℝ– вещественные числа }

3 P Í ℝ² и Р = {(x, y) :x-2 y = x+2y, где x, y Îℝ– вещественные числа }

Вариант №4

1. Р₁ = {(b, 1); (а, 3); (а, 4); (с, 2); (с, 4); (b, 4)}

Р₂ = {(1, 1); (2, 3); (2, 2); (2, 4); (3, 3); (3, 4); (4, 2); (4, 4)}

2. P Í ℝ² и Р = {(x, y) : x² + x = y² + y, где x, y Îℝ– вещественные числа }

3. P Í ℝ² и Р = {(x, y) : x = y-4, где x, y Îℝ– вещественные числа }

Вариант №5

1. Р₁ = {(а, 2); (а, 4); (b, 1); (b, 2); (b, 4); (с, 2); (с, 4)}

Р₂ = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4); (3, 2); (1, 3); (4, 1)}

2. P Í ℝ² и Р = {(x, y) : x – y 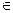ℤ, где x, y Îℝ– вещественные числа }

3. P Í ℝ² и Р = {(x, y) : x² + x = y² , где x, y Îℝ– вещественные числа }

Вариант №6

1. Р₁ = {(а, 2); (а, 4); (а, 3); (с, 1); (с, 2); (с, 3)}

Р₂ = {(1, 1); (1, 4); (2, 3); (3, 3); (4, 1); (4, 3); (4, 4)}

2. P Í ℝ² и Р = {(x, y) : x + y = –2, где x, y Îℝ– вещественные числа }

3. P Í ℝ² и Р = {(x, y) : - x = 2 y, где x, y Îℝ– вещественные числа }

Вариант №7

1. Р₁ = {(а, 1); (b, 2); (b, 3); (с, 1); (с, 3); (с, 4)}

Р₂ = {(1, 1); (1, 2); (1, 3); (2, 2); (2, 3); (3, 3); (3, 4); (4, 1); (4, 4)}

2. P Í ℝ² и P = {(x, y): x²+ y² = 4, x, y Îℝ – вещественные числа }

3. P Í ℝ² и Р = {(x, y) : x -2 y = 4, где x, y Îℝ– вещественные числа }

Вариант №8

1. Р₁ = {(а, 3); (b, 4); (b, 3); (с, 1); (с, 2); (с, 4)}

Р₂ = {(1, 2); (1, 3); (1, 4); (2, 3); (4, 3); (4, 2)}

2. P Í ℝ² , P = {(x, y): y < x –1 и x, y Îℝ – вещественные числа }

3. P Í ℝ² и Р = {(x, y) : x + y <2, где x, y Îℝ– вещественные числа }

Вариант№9

1. Р₁ = {(а, 3); (b, 4); (b, 3); (b, 1); (b, 2); (c, 2)}

Р₂ = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 3); (4, 2)}

2. P Í ℝ² , P = {(x, y): x² = y, где x, y Îℝ – вещественные числа }

3. P Í ℝ² и Р = {(x, y) : 2x² = y² , где x, y Îℝ– вещественные числа }

Вариант №10

1. Р₁ = {(а, 2); (а, 3); (a, 4); (b, 1); (b, 2); (b, 4)}

Р₂ = {(1, 1); (1, 3); (1, 4); (2, 2); (2, 3); (3, 2); (3,3); (4,3); (4,4)}

2. P Í ℝ² , P = {(x, y): x² ³ y, где x, y Îℝ – вещественные числа }

3. РÍ ℝ² и Р = {(x, y) : 2x²+ y²= 3, где x, y Îℝ– вещественные числа }

Вариант №11

1. Р₁ = {(а, 1); (а, 2); (b, 3); (b, 4); (c, 3); (c, 4)}

Р₂ = {(1, 1); (1, 4); (2, 1); (2, 2); (2, 4); (3, 3)}

2. P Í ℤ² , P = {(x, y): x² + y² = 1, где x, yÎℤ – целые числа }

3. РÍ ℝ² и Р = {(x, y) : x + y<- 1, где x, y Îℝ– вещественные числа }

Вариант №12

1. Р₁ = {(а, 2); (а, 3); (а, 4); (с, 3); (c, 1); (c, 4)}

Р₂ = {(1, 4); (2, 3); (2, 1); (3, 4); (4, 2)}

2. PÍℤ², P = {(x, y): x + y – кратно 3, где x, yÎℤ– целые числа}

3. РÍ ℝ² и Р = {(x, y) : x + y<-4, где x, y Îℝ– вещественные числа }

Вариант №13

1. Р₁ = {(а, 1); (а, 2); (а, 4); (b, 2); (b, 4); (c, 3)}

Р₂ = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4);(4,2)}

2. PÍℤ², P = {(x, y): x – y, кратно 2, где х, уÎℤ– целые числа}

3. РÍ ℝ² и Р = {(x, y) : x/2 =y, где x, y Îℝ– вещественные числа }

Вариант №14

1. Р₁ = {(b, 1); (b, 3); (c, 1); (c, 2); (c, 3); (c, 4)}

Р₂ = {(1, 1); (2, 2); (2, 3); (2, 4); (3, 2); (3, 3); (3, 4); (4, 2); (4, 3); (4, 4)}

2. PÍℤ² , P = {(x, y): 2x = 3y, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : 2x<y+1, где x, y Îℝ– вещественные числа }

Вариант №15

1. Р₁ = {(a, 2); (a, 4); (b, 3); (c, 1); (c, 2)}

Р₂ = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 4); (4, 3); (4, 2)}

2. PÍℤ², P = {(x, y): x + y нечетно, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : x³<y+3, где x, y Îℝ– вещественные числа }

Вариант №16

1. Р₁ = {(а, 3); (а, 2); (b, 2); (b, 3); (c, 1); (c, 4)}

Р₂ = {(1, 1); (1, 2); (2, 2); (3, 3); (4, 1); (4, 4)}

2. PÍℤ², P = {(x, y): x – y четно, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : 1/x>y, где x, y Îℝ– вещественные числа }

Вариант №17

1. Р₁ = {(а, 1); (а, 2); (а, 4); (b, 3); (c, 1); (c, 4)}

Р₂ = {(1, 3); (1, 2); (2, 3); (3, 2); (3, 4); (4, 1)}

2. PÍℤ², P = {(x, y): 5x = 2y, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : x+2y=6, где x, y Îℝ– вещественные числа }

Вариант№18

1. P₁={ (a, 1); (b, 3); (c; 1); (c, 4); (c, 3); (c, 2)}

P₂={(1, 1); (1, 2); (1, 4); (2, 1); (2, 2); (2, 3); (3, 3); (3, 2); (3, 4); (4, 3); (4, 4); (4, 1)}

2. P 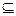ℤ², P = {(x, y): x = –y, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : x +2 y<=-4, где x, y Îℝ– вещественные числа }

Вариант №19

1. P₁={(a, 1); (b, 3); (b, 1); (b, 4); (c, 3); (c, 2)}

P₂={(1, 3); (1, 4); (2, 2); (3, 3); (4, 3); (4, 4);}

2. P 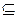ℤ², P = {(x, y): x +1 = y, где x, yÎ ℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : x=>y, где x, y Îℝ– вещественные числа }

Вариант №20

1. P₁={(a, 1); (a, 2); (a; 4); (b, 1); (b, 4); (c, 3)}

P₂={(1, 1); (2, 4); (2, 1); (3, 3); (4, 2); (4, 1)}

2. P 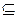ℤ², P = {(x, y): y ≥ x – 2, где x, yÎℤ– целые числа }

3. РÍ ℝ² и Р = {(x, y) : x<1/y, где x, y Îℝ– вещественные числа }

Практическая работа №4.

Тема: Переключательные функции. Способы задания.

Задание №1.

Для f(x,y,z) заданной следующей таблицей истинности удалить несущественную переменную.

Решение:

	x	y	z	f(x,y,z)
¨
¨
¨
¨

Проверим, является ли переменная х существенной. Для этого рассмотрим наборы на которых значения переменных y и z остаются неизменными, а значение переменной х меняется. На наборе (0,0,0) значение функции равно 1, на наборе (1,0,0) значение функции равно 0. Т.е. при неизменных y и z значение функции меняется, если меняется значение х. Значит, переменная х является существенной и её удалять нельзя. Проверим, является ли переменная у существенной. Рассмотрим наборы на которых х и z не меняется, а меняется только у. На наборе (0,0,0) значение функции равно 1, и на наборе (0, 1, 0) значение функции также равно 1. Проверяя все остальные наборы видно, что значение функции не меняется с изменением переменной у, т.е. у несущественная переменная и её можно удалить. Таким же способом проверяется существенность переменной z. По наборам (1,0,0) и (1,0,1) видно, что z существенная переменная. Получается, что у данной функции есть одна несущественная переменная у. Для её удаления необходимо вычеркнуть столбец значений переменной у и строчки в которых эта переменная равна 1. Полученная функция будет эквивалентна исходной и будет зависеть от двух переменных.

Задание №2

Проверьте двумя способами, будут ли эквивалентны следующие формулы: 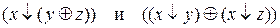. а) составлением таблиц истинности; б) с помощью эквивалентных преобразований.

Решение: а) составим сокращенные таблицы истинности обеих формул:

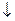x		(y		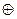z)	(x		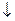y)		(x		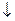z)

Поскольку полученные столбцы не совпадают, формулы не эквивалентны.

б)

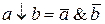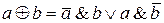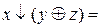
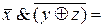
Преобразуем формулы к виду СДНФ. Для этого воспользуемся тождествами: и , где a и b – произвольные формулы. Тогда 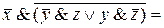(по закону де Моргана) =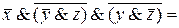 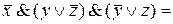(по закону дистрибутивности) = .

.

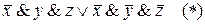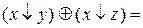
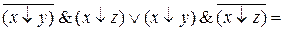
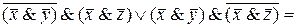
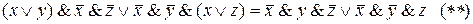Формулы (*) и (**) не совпадают, поэтому исходные формулы не эквивалентны.