Задачи для самостоятельного решения. 6.1. Найти математическое ожидание дискретной случайной величины, имеющей следующее распределение:

6.1. Найти математическое ожидание дискретной случайной величины, имеющей следующее распределение:

а)

Х
Р	0,6	0,3	0,1

б)

Х	-3	-2
Р	0,2	0,4	0,4

в)

Х	-4
Р	0,5	0,4	0,1

6.2. Партия из 10 деталей содержит 4 бракованных. Наугад выбирается две детали. Найти математическое ожидание случайной величины Х, равной числу бракованных деталей среди выбранных.

6.3. Дискретная случайная величина Х принимает три возможных значения: х₁=4 с вероятностью р₁=0,5; х₂=6 с вероятностью р₂=0,3 и х₃ с вероятностью р₃. Найти х₃ и р₃, зная, что М(Х)=8.

6.4. Дискретная случайная величина имеет следующий закон распределения:

Х	х1
Р	0,3	0,5	р3

Математическое ожидание равно 3. Найти х₁ и р₃. Построить многоугольник распределения.

6.5. Найти математическое ожидание величины Z, если

а) Z=3X+4Y; M(X)=2; M(Y)=6.

б) Z=12X+3Y; M(X)=0; M(Y)=4.

6.6. Найти М(Х²) дискретной случайной величины, заданной законом распределения:

а)

Х	-4
Р	0,2	0,3	0,5

б)

Х	0,2	0,5	0,6
Р	0,1	0,5	0,4

6.7. Дан перечень возможных значений дискретной случайной величины: х₁=-1; х₂=0; х₃=1, а также известны М(Х)=0,1 и М(Х²)=0,9. Найти вероятности р₁, р₂, р₃, соответствующие возможным значениям х₁, х₂, х₃.

6.8. Дан перечень возможных значений дискретной случайной величины: х₁=1; х₂=2; х₃=3, а также известны М(Х)=2,3 и М(Х²)=5,9. Найти вероятности р₁, р₂, р₃, соответствующие возможным значениям х₁, х₂, х₃.

6.9. Найти дисперсию и среднеквадратическое отклонение дискретной случайной величины, имеющей следующее распределение:

а)

Х	-5
Р	0,4	0,3	0,1	0,2

б)

Х
Р	0,2	0,3	0,5

в)

Х	-2
Р	0,3	0,1	0,6

6.10. Случайная величина принимает только два значения: 2 и –2 с вероятностями 0,5 и 0,5 соответственно. Определить дисперсию этой случайной величины.

6.11. Дискретная случайная величина имеет только два возможных значения: х₁ и х₂, причем x₁<x₂. Вероятность того, что Х примет значение х₁, равно 0,6. Найти закон распределения величины Х, если М(Х)=1,4; D(X)=0,24.

6.12. Дискретная случайная величина имеет только два возможных значения: х₁ и х₂, причем x₁<x₂. Вероятность того, что Х примет значение х₁, равно 0,2. Найти закон распределения величины Х, если М(Х)=2,6; σ(X)=0,8.

6.13. Проводится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,8. Рассматриваются две случайные величины: Х – разность между числом попаданий и числом промахов; Y – сумма числа попаданий и числа промахов. Построить ряд распределений каждой из этих величин и найти их математические ожидания и дисперсии.

6.14. Плотность распределения непрерывной случайной величины равна f(х)=2х на промежутке (0, 1) и равна нулю вне этого промежутка. Найти функцию распределения, математическое ожидание и дисперсию.

6.15. Плотность распределения постоянна на промежутке [1, 9] и равна нулю вне этого промежутка. Определить значение функции плотности, математическое ожидание и дисперсию.

6.16. Плотность распределения равна 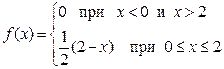. Определить математическое ожидание и дисперсию данной величины.

6.17. Плотность распределения некоторой случайной величины равна 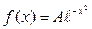. Найти значение А, математическое ожидание и дисперсию.

6.18. Непрерывная случайная величина задана своей функцией распределения 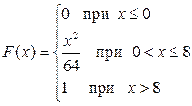. Требуется: а) найти функцию плотности; б) найти математическое ожидание и дисперсию; в) построить графики функции распределения и функции плотности.

6.19. Непрерывная случайная величина задана своей функцией распределения 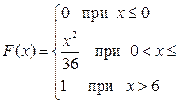. Требуется: а) найти функцию плотности; б) найти математическое ожидание и дисперсию; в) построить графики функции распределения и функции плотности.

6.20. Охотник стреляет по дичи до первого попадания, но успевает делать не более четырех выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

6.21. На заводе работают четыре автоматические линии. Вероятность того, что в течение рабочей смены первая линия не потребует регулировки, равна 0,9, вторая – 0,8, третья – 0,75, четвертая – 0,7. Найти математическое ожидание числа линий, которые в течение рабочей смены не потребуют регулировки.

6.22. Случайная величина Х задана плотностью распределения 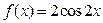в интервале 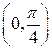; вне этого интервала плотность равна нулю. Найти моду и медиану данной случайной величины.

6.23. Случайная величина Х в интервале 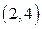задана плотностью распределения 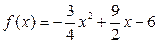; вне этого интервала плотность равна нулю. Найти моду, математическое ожидание и медиану случайной величины.

6.24. Случайная величина Х в интервале 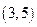задана плотностью распределения 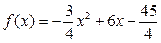; вне этого интервала плотность равна нулю. Найти моду, математическое ожидание и медиану случайной величины.

6.25. Случайная величина Х в интервале 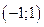задана плотностью распределения 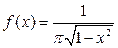; вне этого интервала плотность равна нулю. Найти моду и медиану данной случайной величины.

6.26. Случайная величина Х в интервале 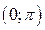задана плотностью распределения 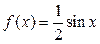; вне этого интервала плотность равна нулю. Найти дисперсию данной случайной величины.

6.27. Случайная величина Х в интервале 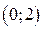задана плотностью распределения 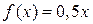; вне этого интервала плотность равна нулю. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков данной случайной величины.

6.28. Случайная величина Х в интервале 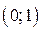задана плотностью распределения ; вне этого интервала плотность равна нулю. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков данной случайной величины, асимметрию и эксцесс.