Понятие о математическом описании дискретных автоматов

Существуют два подхода к определению дискретного автомата - макроподход и микроподход.

При макроподходе, когда интересует только внешнее поведение автомата – реакция автомата на входные сигналы. Дискретный автомат определяют либо в виде совокупности функций, либо в виде конечного ориентированного графа, либо в алгебраической форме.

При микроподходе дискретный автомат задается множеством элементов и схемой их соединения. В этом случае кроме функционирования описывается и строение автомата, и автомат называется структурным.

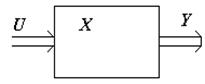Рис. 1.2 Структурная схема дискретного автомата

При макроподходе внешние воздействия, выходная реакция и состояния рассматриваются как буквы трех алфавитов, называемых соответственно входным алфавитом 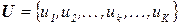, выходным алфавитом 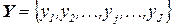и алфавитом состояния 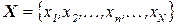. Примером входного и выходного алфавитов является бинарный (двоичный) алфавит, содержащий только две буквы - 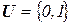, 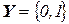. Закон функционирования автомата может быть задан двумя функциями – функцией переходов 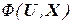, связывающей пару "входная буква – состояние" и отображающей множество 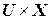в 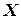, а также функцией выходов 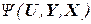, связывающей пару "выходная буква – состояние" и отображающей множество 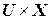в 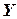, соответственно.

Таким образом, дискретный автомат полностью описывается множеством 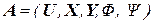входного и выходного алфавитами, алфавитом состояния, функциями переходов и выходов и обозначается.

В каждый из моментов дискретного времени 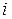автомат, находящийся в определенном состоянии, воспринимает входной сигнал - букву входного алфавита 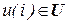, выдает выходной сигнал 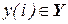- букву выходного алфавита, определяемую функцией выходов 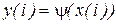, и переходит в новое состояние, определяемое функцией переходов .

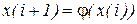Поведение автомата - математическое понятие, описывающее взаимодействие автомата с внешней средой.

В зависимости от типа поведения дискретные автоматы подразделяются на преобразователи, рецепторы (распознаватели) и генераторы.

Для определения поведения автомата функции перехода и выхода распространяют на множество 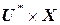, где 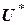- множество всех слов входного алфавита, включая пустое слово :

;

.

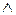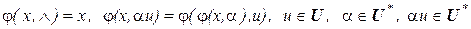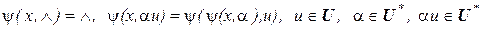Запись 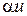обозначает слово, получаемое из слова 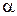приписыванием буквы 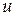. Функци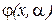и и 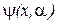для произвольного состояния 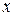и произвольного входного слова 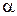описывает состояние, в которое переходит автомат из состояния 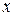под действием входного слова 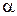, и выходную букву, которая выдается автоматом в момент поступления последней буквы входного слова .

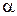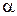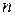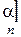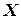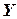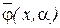Введем обозначение начальной части слова длиной как , и слов в алфавитах и - и 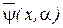, определяемые как:

;

.

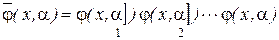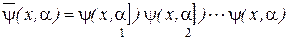Функци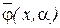и и 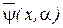описывают последовательность всех состояний, в которые переходит автомат из состояния 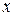под воздействием слова 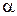, и выдаваемое автоматом выходное слово.

Таким образом совокупность начального состояния автомата 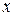, последовательности состояний 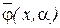, в которые переходит автомат под воздействием входного слова 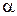, выходного слова 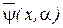является функционированием дискретного автомата 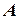и обозначается как

.

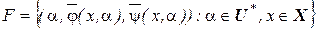Автомат с выделенным начальным состоянием 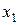называется инициальным и обозначается .

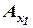Для инициального автомата-преобразователя основное значение в его функционировании имеет функция 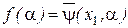, отображающая слова входного алфавита 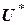в слова выходного алфавита .

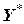Для инициального автомата-акцептора подмножество входного множества 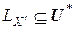, определенное для выделенного подмножества заключительных состояний автомата 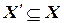, определяется как

.

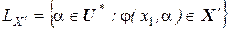Классификация дискретных устройств

По объему памяти. Устройства описываются моделями

- без памяти;

- с конечной памятью;

- с бесконечной памятью.

Без памяти – комбинационные устройства. В таких устройствах выходные значения сигналов определяются только входными сигналами и не зависят от внутреннего состояния. Считают, что такое устройство имеет одно состояние.

С конечной памятью. Эти устройства обладают конечным числом внутренних состояний. Выходной сигнал определяется не только входным сигналом, но и состоянием, в котором находится устройство. К таким устройствам относятся устройства автоматики, контроля, управления и отдельные узлы вычислительных машин.

Автоматы с бесконечной памятью являются идеализированными моделями вычислительных машин, так как они имеют столь большое количество внутренних состояний, что их практически невозможно пересчитать.

По способу функционирования дискретные устройств делятся на

- детерминированные;

- вероятностные.

По способу формирования выходного сигнала.

Дискретный автомат, для которого выходной сигнал зависит от входного сигнала и состояния, то есть 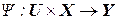, называется автоматом Мили.

Дискретный автомат, для которого выходной сигнал зависит только от состояния и не зависит от входного сигнала, то есть 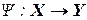, называется автоматом Мура.

По способу ввода входной информации дискретные устройства подразделяются на

- автономные;

- неавтономные.

Первые не получают внешней информации в процессе функционирования. Такой режим работы характерен для ЭВМ после загрузки перерабатываемой информации в память машины. Вторые получают информацию по входным каналам.

Доцент к. т. н., доцент В.Трофименко

[1] Математическая энциклопедия. Ред. коллегия: И. М. Виноградов (глав. ред.) [и др.] Т. 1 – М., "Советская энциклопедия", 1977