Элементы эконометрической модели и их свойства

Вид функции j называется спецификацией модели. Модель (1) является частным видом эконометрической модели, в которой спецификация линейная. Функция j описывает общий ход экономического процесса, экономическую тенденцию развития, изменения зависимого показателя при изменении независимого.

Величина x – называется независимой или объясняющей переменной;

Величина y называется зависимой или объясняемой переменной. Значение величины y_k состоит из двух частей:

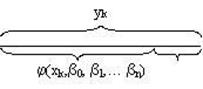
величина j(x_k,b₀, b₁,… b_n) – это часть зависимого показателя, обусловленная или объяснённая экономическими причинами или просто объясняемая часть; e_k – необъяснённая часть, поскольку невозможно описать все случайные факторы.

e_k – величина, выражающая вклад случайных мелких, незначительных факторов, которые отклоняют реальные статистические данные от значений зависимого показателя, обусловленного экономической тенденцией, однако не изменяют эту экономическую тенденцию.

Основные свойства величин e_k:

1) эти величины случайные, в противном случае зависимость (2) функциональная;

2) e_k принимают положительные и отрицательные значения, так как случайные факторы увеличивают или уменьшают величины, обусловленные экономической тенденцией;

3) Абсолютные величины |e_k| не должны быть очень большими по сравнению со значениями, вычисляемыми по спецификации. Другими словами, необъяснённая часть показателя y должна быть мала по сравнению с объяснённой. Если же отклонения значительны, тогда спецификация j неточно описывает экономическую тенденцию, её необходимо уточнять и в число объясняющих факторов вводить факторы, вклад которых приводит к большим значениям e_k.

b₀, b₁,…, b_k – параметры спецификации. Для разных видов функции j количество этих параметров, их смысл и названия разные. Например, для линейной спецификации

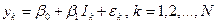
этих параметров два;

параметр

b₀ – свободный член,

b₁ – угловой коэффициент.

Задачи эконометрики

1) По имеющимся статистическим данным подбор спецификации, наиболее точно отражающей экономическую тенденцию. Эта задача может быть уже решена экономической или эконометрической теорией.

2) Оценивание параметров спецификации b₀, b₁,…, b_k и определение качества этих оценок и эконометрической модели в целом. (Насколько хорошо модель объясняет изменение показателя y).

3) Формирование прогнозов на основе построенной модели и выработка рекомендаций для эффективных экономических решений.

Эконометрика и её место в ряду математических и экономических дисциплин

Название «эконометрика» было введено в 1910 г. бухгалтером П.Цьемпой. Цьемпа считал, что если к бухгалтерском учёту применить методы алгебры и геометрии, то можно получать новые, более глубокие экономические знания.

Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика». Таким образом, эконометрика является наукой об измерении и статистическом количественном анализе экономических явлений.

Эта наука является сплавом трёх компонент: экономической теории, экономической и математической статистики.

Тема 1 Методы и модели регрессионного анализа

Цели и задачи изучения темы:

Формирование представления о регрессионной зависимости, о методах, принципах и моделях регрессионного анализа, о линейной регрессии, о нелинейных моделях регрессии и их линеаризации, о парной и множественной регрессии.

В эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика, прежде всего, связана с методами регрессии и корреляции.

Основные понятия регрессионного анализа

Регрессионной (корреляционной) зависимостью называют зависимость между значением одной переменной и условным математическим ожиданием (средним значением) другой.

В естественных науках часто речь идет о функциональной зависимости (связи), когда каждому значению одной переменной соответствует вполне определенное значение другой (например, скорость свободного падения в вакууме в зависимости от времени и т.д.).

В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной.

Возникновение такой зависимости обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п.

В силу неоднозначности зависимости между Y и X для исследователя, в частности, представляет интерес усредненная по X схема зависимости, т. е. закономерность в изменении условного математического ожидания M_X(Y) или M(Y/X = x) в зависимости от х.

Если зависимость между двумя переменными такова, что каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной или регрессионной.

Иначе, корреляционной зависимостьюмежду двумя переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Корреляционная зависимость может быть представлена в виде

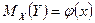
или

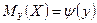
где j(x) ¹ const, y(y) ¹ const.

В регрессионном анализе рассматриваются односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной X. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении X соответствующие значения Y подвержены случайному разбросу за счет действия ряда неконтролируемых факторов.

При этом зависимую переменную Y называют также функцией отклика, объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком, а независимую переменную X – объясняющей, входной предсказывающей, предикторной, экзогенной переменной, фактором, регрессором, факторным признаком.

Уравнение

M_x(Y) = j(x, b₀, b₁,…, b_n)

называется модельным уравнением регрессии (или просто уравнением регрессии), а функция j(х) – модельной функцией регрессии (или просто функцией регрессии), а ее график — модельной линией регрессии (или просто линией регрессии). b₀, b₁,…, b_n – параметры функциональной зависимости.

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная X примет значение х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (х_i , у_i) ограниченного объема п. В этом случае речь может идти только об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная функция (кривая) регрессии:

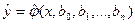
где 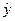-– выборочное условное среднее переменной Y при фиксированном значении переменной Х= х, b₀, b₁,…,b_n –параметры функции .

Это уравнение называется выборочным уравнением регрессии или моделью регрессионной зависимости Y от X.

Вид функции 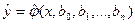называется спецификацией модели выборочной регрессии.

Задачами регрессионного анализа являются следующие:

1. Оценка (выбор) спецификации модели – установление конкретного выражения функции 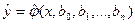. Достаточно часто эта задача может быть решена точно в том случае, если заранее известен характер изменения величины Y при изменении X: линейный, экспоненциальный,… Вид зависимости может быть известен теоретически, как результат уже проводившихся исследований или определён визуально при анализе статистических данных (х_i , у_i). Например, для выборки, представленной на следующей диаграмме

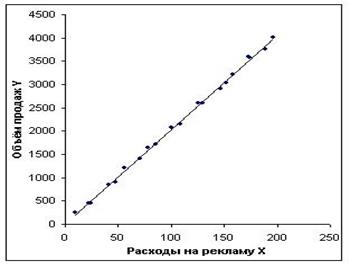
линейный характер зависимости очевиден.

2. После выбора спецификации производится оценка параметров спецификации b₀, b₁,…,b_n. Для разных спецификаций набор параметров различен. Например, при выборе линейной спецификации

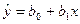
следует вычислить два параметра: b₀, b₁. Даже в том случае, если спецификация модели определена точно, значения b₀, b₁ будут являться только оценками истинных параметров уравнения регрессии

y = b₀ + bx.

3. Производится оценка качества полученной регрессии.

Сформулируем основные предпосылки и принципы регрессионного анализа.

1. Объективно существует зависимость одного экономического показателя Y от другого X. Эта зависимость не функциональная, так как на основное течение процесса, экономическую тенденцию накладываются различные случайные факторы. Поэтому для данного значения независимого показателя Х = х зависимый показатель может принять значение из некоторого множества с какой-то вероятностью. То есть для каждого значения Х величина Y является случайной величиной, распределённой по некоторому закону.

2. Значит, каждому значению Х соответствует условное математическое ожидание M_x(Y). То есть функциональной является зависимость не самого значения Y от Х, а его условного математического ожидания: M_x(Y) = j(x, b₀, b₁,…, b_n). Эта зависимость называется модельной регрессией. В общем случае ни вид функции, ни точные значения параметров b₀, b₁,…, b_n неизвестны, поскольку недоступны генеральные совокупности значений переменной Y при заданных Х.

3. Реальным выражением зависимости Y от X является статистическая выборка (x_i,y_i). По этой выборке методами регрессионного анализа получают приближённую функциональную зависимость 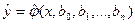выборочного условного среднего Y от х.

4. Функциональным зависимостям

M_x(Y) = j(x, b₀, b₁,…, b_n),

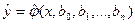
соответствуют модели наблюдений – зависимости между реальными статистическими данными (x_i,y_i):

y_i = j(x_i, b₀, b₁,…, b_n) + e_i,

,

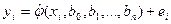где e_i = y_i – j(x_i, b₀, b₁,…, b_n) = y_i – M_xi(Y) – отклонение наблюдаемого значения y_i от своего условного математического ожидания;

e_i – ошибка, возмущение – результат воздействия неучтённых факторов;

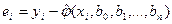– отклонение наблюдаемого значения y_i от вычисленного по теоретической функции регрессии; фактически невязки e_i являются выборочными значениями величин e_i.

e_i – невязка.

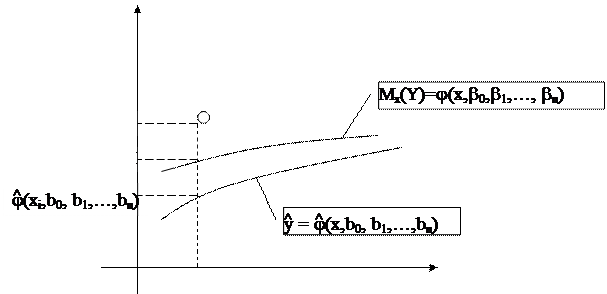Методы регрессионного анализа используются для подбора по возможности более точной спецификации 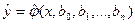и оценок параметров b₀, b₁,…,b_n с тем, чтобы выборочная линия регрессии 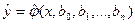приближалась к модельной j(x,b₀,b₁,…, b_n).

Спецификация модели

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными — у и х, т.е. модель вида

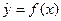
Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида

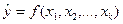
Рассмотрим возможности применения методов простой или парной регрессии и корреляции в эконометрике.

Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами исследование начинается с теории, устанавливающей связь между явлениями.

Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза, о том, что величина спроса у на товар А находится в обратной зависимости от цены х, т.е. 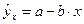. В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. Так, если зависимость спроса у от цены х характеризуется, например, уравнением 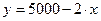, то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:

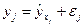
где 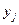- фактическое значение результативного признака;

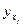- теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т.е. из уравнения регрессии;

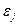- случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина ε называется также возмущением. Она включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

Приведенное ранее уравнение зависимости спроса у от цены х точнее следует записывать как

,

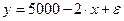поскольку всегда есть место для действия случайности. Обратная зависимость спроса от цены не обязательно характеризуется линейной функцией

.

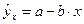Возможны и другие соотношения, например:

.

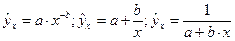Поэтому от правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 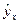подходят к фактическим данным у.

К ошибкам спецификации будет относиться не только неправильный выбор той или иной математической функции для 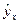, но и недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки - увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.