Непрерывность функции в точке. Пусть функция определена в некоторой окрестности точки х0

Пусть функция определена в некоторой окрестности точки х0, функция y=f(x) называется непрерывной в точке х0, если существует предел в этой точке и он равен значению функции в этой точке.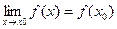

Замечание: для непрерывной функции можно переставить знак функции и предела, т.е.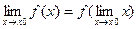

Dх=х-х0 – приращение аргумента функции.

Dy=f(x)-f(x0)=f(x0+Dx)-f(x0) – приращение функции, вызванное приращением аргумента.

Определение: функция y=f(x) называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Непрерывность функции в интервале и на отрезке

функция y=f(x) называется непрерывной в интервале от a до b (a;b), если она непрерывна в каждой точке этого интервала.

Функция y=f(x) называется непрерывной на отрезке [a;b], если она непрерывна в каждой точке интервала (a;b) и в точке х=а непрерывна справа, а в точке х=b непрерывна слева.

Классификация точек разрыва

Если в точке х0 условие непрерывности нарушается, то говорят, что функция в точке х0 терпит разрыв/имеет точку разрыва.

Условие непрерывности: предел справа существует и конечен, предел слева существует и конечен, они равны между собой и равны значению функции в точке.

Точка х0 называется точкой разрыва первого рода, если в этой точке существуют конечные пределы функции справа и слева, но не равны значению функции; если эти пределы равны, то разрыв называется устранимым.

Точка х0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или бесконечен.

Свойства функций, непрерывных в точке

Пусть f(x) и g(x) определены в некоторой окрестности х0 и непрерывны в точке х0, тогда 1. функции f+g, f*g, непрерывны в точке х0, а функция f/g непрерывна, если g(x0)¹0.

2. Функция g(f(x)) непрерывна в точке х0 (суперпозиция)

3. элементарные функции непрерывны во всех точках своей области определения, в окрестностях которых они определены.

Свойства функций, непрерывных на отрезке (a;b)

Функция f(x) называется ограниченной на отрезке [a;b], если существует такое c=const, c>0, что модуль функции |f(x)|£c для всех xÎ[a;b], в противном случае функция называется неограниченной на отрезке.

Теорема: всякая непрерывная на отрезке [a;b] функция ограничена на отрезке [a;b]

Теорема Вейерштрасса: если функция непрерывна на [a;b], то она достигает на этом отрезке своего наибольшего и наименьшего значения.

Теорема: если функция непрерывна на [a;b] и на его концах принимает значения разных знаков, то внутри отрезка найдётся хотя бы одна точка с, значение функции в которой равно 0.

Дифференцирование

Понятие производной

Рассмотрим функцию y=f(x) на интервале (a;b). Возьмём на этом интервале точку х0 и приращение на оси Ох. Прямая, соединяющая 2 точки (х0;f(x0)) и (x0+Dx;f(x0+Dx))на графике функции называется секущей.

Угловой коэффициент секущей равен отношению приращения функции к вызвавшему его приращению аргумента.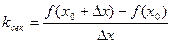

Производной функции y=f(x) называется предел отношения приращения функции к вызвавшему его приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует)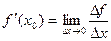

Если предел конечен, то производная конечная, если предел бесконечен, то производная бесконечна.