Дифракция на пространственных структурах

Рентгеноструктурный анализ.

Мы знаем формулу дифракционной решётки, по которой можно определить длину волны света, если известен период решётки. Но по этой же формуле можно решить обратную задачу: найти период решётки, если известна длина волны излучения. Эта идея нашла применение в задаче определения расстояния между атомами в кристалле и определении порядка из расположения. Но поскольку расстояние между атомами в кристалле очень мало, то видимый свет для этого не годится, так как длина его волны для этого слишком велика. Для этого используют рентгеновские лучи. Их длина волны соизмерима с расстоянием между атомами в кристалле, кроме того, они обладают высокой проницаемостью и ими можно исследовать все кристаллы, даже непрозрачные для видимых лучей. Таким образом, просвечивая рентгеновскими лучами кристаллы и исследуя дифракционную картину можно узнать расстояние между атомами в кристалле и узнать о порядке их расположения в кристалле. Такой метод называетсярентгеноструктурным анализом.

Следует также отметить, что атомы в кристалле расположены в трёхмерном пространстве, поэтому и дифракционная картина будет также отображать трёхмерное расположение атомов. Кристаллическую решётку можно представить как множество плоскостей, находящихся на одинаковом расстоянии друг от друга. Выбор множества плоскостей зависит от направления на кристалл луча. В свою очередь, каждая плоскость может также рассматриваться как двумерная дифракционная решётка, в которой источником дифракционных максимумов служат отдельные атомы.

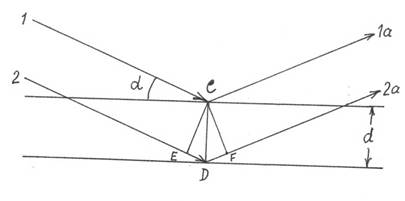
Представим себе, что лучи 1и 2 падают на кристалл под очень малым углом. Тогда рассеянные дифракцией лучи 1аи 2ададут максимум в том случае, если разность их хода D = DE + DF = 2dsinaбудет равна целому числу длин волн излучения: 2dsina = kl.

Иными словами, лучи, рассеянные кристаллом, дадут картину чередующихся максимумов и минимумов, аналогично дифракционной картине, наблюдаемой в видимых лучах. Данное явление на опыте впервые наблюдал в 1912 году Макс фон Лауэ с коллегами. На этом опыте они доказали, что рентгеновские лучи имеют волновую природу. С тех пор дифракционную картину рентгеновских лучей на монокристалле стали называть лауэграммой.По лауэграмме можно узнать не только расстояние между атомами, но и порядок их расположения в кристалле. Такой метод исследования получил название рентгеноструктурного анализа.

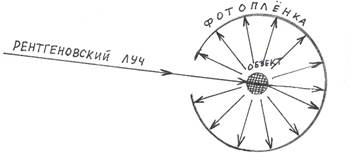
В 1916 году Дебай и Шерер разработали метод рентгеноструктурного анализа для поликристаллических веществ. Для этого измельчённое в порошок вещество помещали в специальную пробирку и помещали её вдоль оси, цилиндра, образованного светочувствительной фотоплёнкой. И при этом получали картину лучей, рассеянных препаратом на все 360^о. Таким образом, была расшифрована структура белка и других органических веществ.

Разрешающая способность оптических приборов.

Теория Аббе.

Волновые свойства света проявляются при построении действительного изображения в микроскопе и телескопе. Рассмотрим микроскоп. Изображение микропрепарата создаётся объективом и рассматривается окуляром. Однако известно, что оптический микроскоп имеет наибольшее увеличение только до 2000 раз. Казалось бы, чего проще: сделать трубу микроскопа в несколько раз длиннее и обеспечено увеличение хоть в десять тысяч раз! Но если бы мы сделали такой микроскоп и получили бы увеличение действительно в 10000 раз, то мы бы в объекте ничего нового не рассмотрели бы, так как изображение не только стало бы крупнее, но и стало бы более расплывчатым, размытым. А причиной этого служит волновая природа света. Как ни старайся, а против волновой природы света ничего поделать невозможно. Существует так называемый предел разрешениямикроскопа. Иными словами, предел разрешения микроскопа – это минимальное расстояние между двумя точками объекта, которые ещё могут быть видимы раздельно.

Учёный Аббе разработал теорию, которая объясняет предел разрешения оптического микроскопа. Согласно его теории для правильной передачи изображения объекта, нужно, чтобы в объектив попали не только лучи, дающие главный, центральный максимум, но и максимум, хотя бы 1-го порядка.

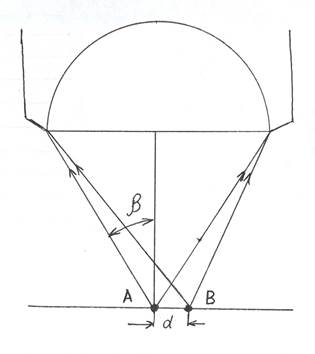
Попробуем на эту проблему посмотреть с другой точки зрения. Представим себе, что под микроскопом рассматриваются две точки Аи Ви расстояние между ними d. Если бы лучи от точек АиВшли к краям объектива абсолютно в одних фазах, то их действительные изображения слились бы в одну точку и мы эти точки видели бы как одну, то есть они были бы неразрешены. Попробуем выяснить, при каком минимальном расстоянии между ними они уже будут различаться по отдельности. Это уже будет возможно в том случае, когда лучи от этих точек придут к краям объектива с разностью хода минимум в одну длину волны. Или, согласно формуле, выведенной для дифракционной решётки, dsinb=kl. В данном случае достаточно, чтобы k=1.

Тогда: dsinb=l.

Тогда предел разрешения микроскопа будет выражаться формулой:

d=l/sinb

Мы заинтересованы в том, чтобы d было как можно меньше. А для этого надо, чтобы длина световой волны была как можно меньше, а угол b - как можно больше. Это можно достичь либо увеличением диаметра объектива, либо уменьшением расстояния от объекта до объектива Угол bназывается апертурным.

Голография.

Высокая монохроматичность и когерентность лазерного излучения позволяет использовать дифракцию для записи на фотоматериале объёмного изображения различных объектов. Этот процесс называется голографией.

Рассмотрим более подробно этот процесс.

Направим на фотопластинку два лазерных луча от одного и того же лазера. Но при этом, один из них широким пучком падает непосредственно на фотопластинку, а другой падает еа ту же пластинку, предварительно отразившись от записываемого объекта. Таким образом, на пластинке встречаются два луча: один идущий непосредственно от лазера, а другой – отражённый от объекта.

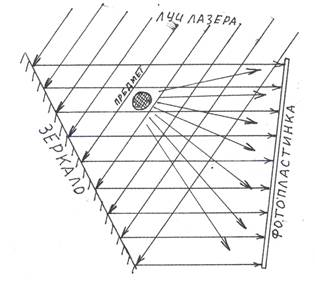И эти лучи интерферируют, при этом фотоэмульсия эту интерференционную картину запечатлевает. После проявления этой фотопластинки на ней видны на просвет мелкие полосы, расположенные хаотично. При этом ничего, похожего на изображение данного предмета на пластинке не просматривается. На самом деле в этом хаосе мелких линий зашифрована информация о предмете: о его форме и о его положении. Пластинка с такой информацией называется голограммой. И для того, чтобы это изображение сделать видимым, нужен снова лазерный луч.

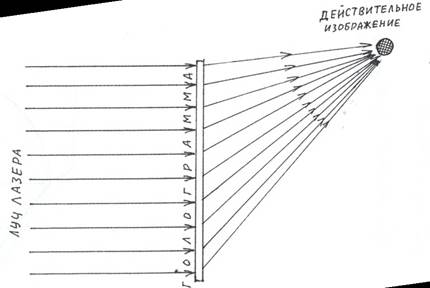
При просвечивании лазерным лучом этой голограммы, лучи, вследствие дифракции, создадут действительное изображение предмета. Причём, изображение будет трёхмерным, объёмным, его можно рассмотреть со всех сторон. Максимумы второго порядка создадут изображение второго порядка и т.д.

Голограмму можно создать и на зеркальной поверхности, это будет отражательная голограмма. В настоящее время отражательные голограммы применяются не только в научных целях, но и для украшения различных значков и сувениров, для маркировки ценных бумаг и лицензионных товаров.

Но всё-таки наиболее широкое применение голография находит в научных исследованиях.

Контрольные вопросы