Структурные средние: медиана и мода

Медианой называется значение ряда, стоящее в центре ранжированного ряда (т.е. выстроенного в порядке возрастания или убывания случайной величины). При этом число единиц совокупности с большим и меньшим, чем медиана, значением одинаково.

Если всем единицам ранжированного ряда придать порядковые номера, то номер медианы в ряду с нечетным числом членов n определяется как (n+1)/2. Так, в ряду из 81 члена номер медианы (81+1)/2, т.е. медианой является значение ряда, стоящее под номером 41.

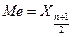, если n – нечетное.

Если число членов ряда четное, то медиану приходится определять как среднюю двух центральных значений ранжированного ряда, порядковые номера которых n/2 и n/2+1. Так, если в ряду 80 значений, то центральными будут ранжированные значения с порядковыми номерами 80/2=40 и 80/2+1=41. При большой длине ряда (n > 100) выбирают значение медианы как X_i с порядковым номером n/2.

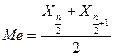, если n – четное.

В случае неточных или экстремальных крайних значений ряда среднее арифметическое становится ненадежным, в то время как медиана от величины крайних значений ряда при условии его ранжирования не зависит. Поэтому медиану рекомендуется определять как дополнение к среднему арифметическому при асимметричных распределениях.

Медиана может определяться графически из интегральной кривой распределения: она будет равна абсциссе точки, где величина накопленной вероятности 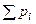= 50%, т.е Р(Х<Me) = P(X>Me). На медиану, определяемую как значение переменной, которому соответствует средняя точка на кривой распределения накопленных частот, влияет не величина экстремальных значений СВ, а их число в распределении случайной величины.

Мода – это наиболее часто встречающееся (т.е. наиболее вероятное) значение случайной величины. Экстремальные значения СВ не оказывают влияния на моду, которая определяется как наиболее вероятное значение случайной величины. Моду рекомендуется определять при резко асимметричных распределениях, для которых среднее арифметическое не является типичным значением СВ в том смысле, что наибольшая повторяемость не приходится на интервалы значений СВ, близкие к среднему.

Модальный интервал – это интервал с наибольшей повторяемостью. Внутри интервала мода определяется по формуле

,

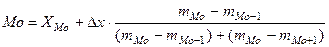где Mo – мода, X_Mo – нижняя граница модального интервала, 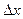– величина интервала, m_Mo – частота модального интервала, m_Mo-1 – частота интервала, предшествующего модальному, m_Mo+1 – частота интервала, следующего за модальным. Формула пригодна только для расчета моды в рядах с равными интервалами.

В качестве приближенного значения моды наиболее часто используют середину интервала с наибольшей повторяемостью ряда распределений. Тогда мода может определяться графически по дифференциальной кривой распределения, как абсцисса максимума этой кривой.

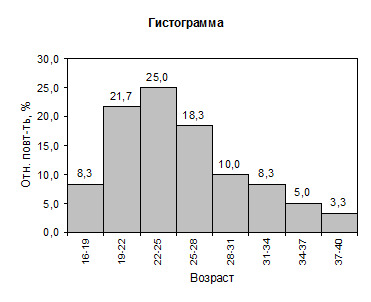
Более точно мода может определяться графически по гистограмме распределения. Для этого используются три соседних столбца гистограммы: самый высокий и два прилегающих к нему слева и справа. Модой является абсцисса точки пересечения крест-накрест отрезков, соединяющих верхние граничные точки самого высоко столбца гистограммы с границами соседних столбцов гистограммы.

Для не очень асимметричных и одновершинных распределений связь между средней, медианой и модой определяется соотношением

.
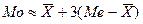