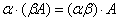Матрицы. Линейные операции над ними и их свойства

ВОПРОСЫ ПО ВЫШКЕ

1.Матрицы и операции над ними и их свойства. Определитель матрицы порядков 2 и 3 и в общем случае.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

§ сложение матриц, имеющих один и тот же размер;

§ умножение матриц подходящего размера (мат-у, имеющую 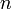столбцов, можно умножить справа на матрицу, имеющую 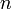строк);

§ умножение матрицы на элемент основного кольца или поля (т. е. скаляр).

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.

Матрицы. Линейные операции над ними и их свойства.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

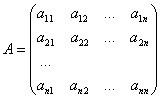
Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной.

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.

Матрица, у которой все элементы равны нулю, называется нулевой.

1.

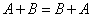
2.

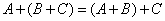
3.

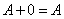
4.

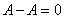
5.

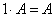
6.

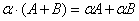
7.

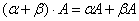
8.