Вопрос 17. Вероятностный смысл мат. ожидания. Математическое ожидание числа появлений события в независимых испытаниях

X	x1	x2	…	xk
	m1	m2		mk

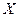приняло значение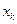 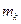раз.

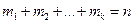
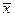- среднее арифметическое случайной величины.

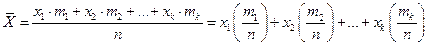
значение в скобках – относительная частота появления.

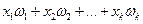
Как будит доказано далее при большом 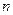(число испытаний) значения 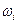стремятся к их вероятностям.

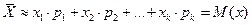
Следовательно математическое ожидание приближенно равно среднему арифметическому всех наблюдаемых значений и чем больше значений 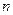тем ближеоно к среднему значению.

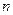- количество испытаний

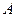- испытания, событие

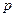- вероятность одинакова

теорема: математическое ожидание числа появлений события 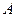в 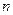независимых испытаниях равна произведению.

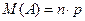
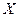- случайная величина равная числу появления события 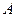в 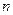независимых испытаниях.

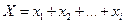
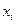- случайная величина равная числу появления события 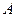в отдельно взятом 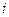ом испытании.

xi
p	1-p	p

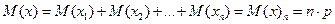
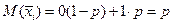
Вопрос 18. Дисперсия дискретной случайной величины и ее свойства.Введем случайную величину представляющую собой отклонение 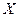от математического ожидания.

X	x1	x2	…	xn
p	p1	p2		pn

			…

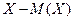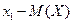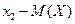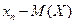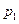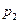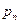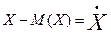- центрированная случайная величина. 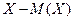- центрированная математическая величина. 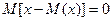Докажем что математическое ожидание отклонения равно 0.

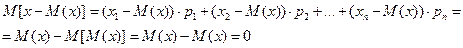
Так как математическое ожидание равно 0 как положительное так и отрицательное значение и тем самым они взаимнопогашаются. Будем рассматривать математическое ожидание квадрата отклонения.

Дисперсией случайной величины 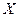называют математическое ожидание квадрата её отклонения.

		…

		…

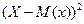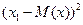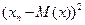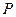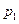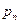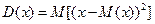
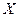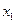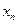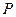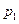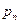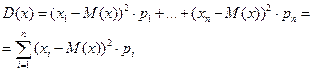
теорема: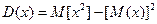

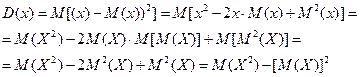
Теорема доказана.

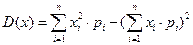
Свойства дисперсии:

1) 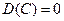от константы.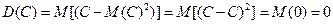

2)

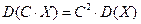
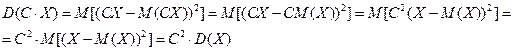
3) Дисперсия двух независимых величин равна сумме соответствующих дисперсий.

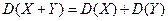
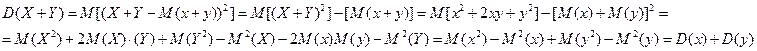4) 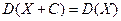(из первого и второго свойства)

5)

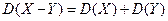
Вопрос 19. Дисперсия числа появления событий в независимых испытаниях. Среднее квадратическое отклонение.

Дисперсия числа появления событий в независимых испытаниях.

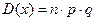вероятность появления события в каждом испытании одинаково.

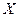- случайная величина равная числу появления события 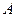в 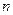независимых испытаниях.

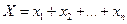
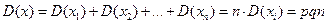
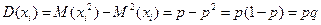
Среднее квадратическое отклонение.

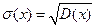- среднеквадратическое отклонение

свойство: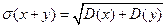

теорема 1:

Пусть даны 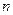независимые величины, причём случайные величины одинаково распрелелены.

Тогда математическое ожидание их среднего арифметического 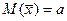где 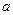- математическое ожидание каждой из случайных величин.

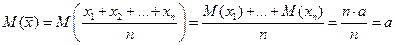
теорема 2:

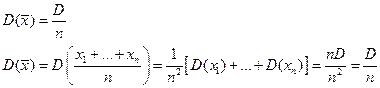
теорема 3:

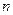- число случайных величин