ИДЗ – 3 Приложения производной
Индивидуальные домашние задания
ИДЗ – 1 Вычисление производных
1Найти производные данных функций:
1.1а) 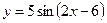 , б)
, б) 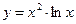 , в)
, в) 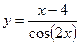 .
.
1.2а) 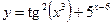 , б)
, б) 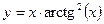 , в)
, в) 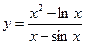 .
.
1.3а) 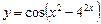 , б)
, б) 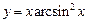 , в)
, в) 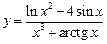 .
.
1.4а) 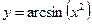 , б)
, б) 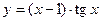 , в)
, в) 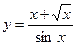 .
.
1.5а) 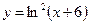 , б)
, б) 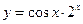 , в)
, в) 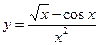 .
.
1.6а) 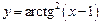 , б)
, б) 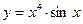 , в)
, в) 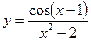 .
.
1.7а) 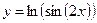 , б)
, б) 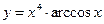 , в)
, в) 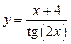 .
.
1.8а) 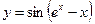 , б)
, б) 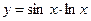 , в)
, в) 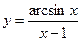 .
.
1.9а) 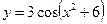 , б)
, б) 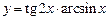 , в)
, в) 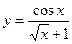 .
.
1.10а) 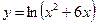 , б)
, б) 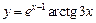 , в)
, в) 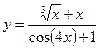 .
.
1.11а) 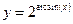 , б)
, б) 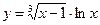 , в)
, в) 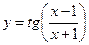 .
.
1.12а) 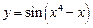 , б)
, б) 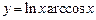 , в)
, в) 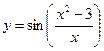 .
.
1.13а) 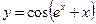 , б)
, б) 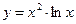 , в)
, в) 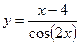 .
.
1.14а) 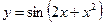 , б)
, б) 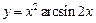 , в)
, в) 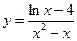 .
.
1.15а) 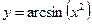 , б)
, б) 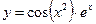 , в)
, в) 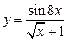 .
.
1.16а) 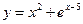 , б)
, б) 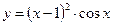 , в)
, в) 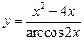 .
.
1.17а) 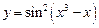 , б)
, б) 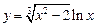 , в)
, в) 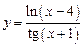 .
.
1.18а) 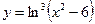 , б)
, б) 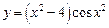 , в)
, в) 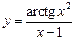 .
.
1.19а) 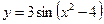 , б)
, б) 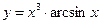 , в)
, в) 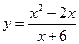 .
.
1.20 а) 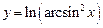 , б)
, б) 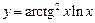 , в)
, в) 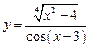 .
.
1.21а) 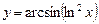 , б)
, б) 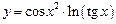 , в)
, в) 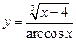 .
.
1.22а) 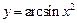 , б)
, б) 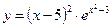 , в)
, в) 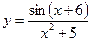 .
.
1.23 а) 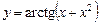 , б)
, б) 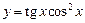 , в)
, в) 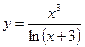 .
.
1.24а) 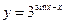 , б)
, б) 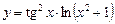 , в)
, в) 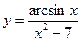 .
.
1.25а) 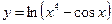 , б)
, б) 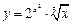 , в)
, в) 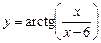 .
.
1.26а) 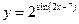 , б)
, б) 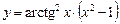 , в)
, в) 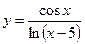 .
.
1.27а) 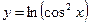 , б)
, б) 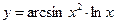 , в)
, в) 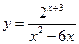 .
.
1.28а) 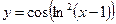 , б)
, б) 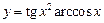 , в)
, в) 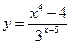 .
.
1.29а) 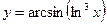 , б)
, б) 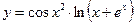 , в)
, в) 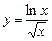 .
.
1.30а) 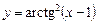 , б)
, б) 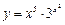 , в)
, в) 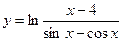 .
.
2 Найти производную неявной функции:
2.1 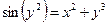 .
.
2.2 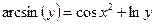 .
.
2.3 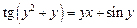 .
.
2.4 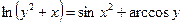 .
.
2.5 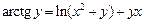 .
.
2.6 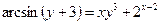 .
.
2.7 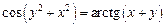 .
.
2.8 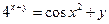 .
.
2.9 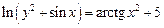 .
.
2.10 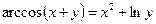 .
.
2.11 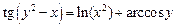 .
.
2.12 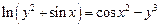 .
.
2.13 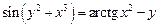 .
.
2.14 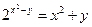 .
.
2.15 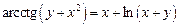 .
.
2.16 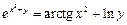 .
.
2.17 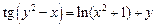 .
.
2.18 .
2.19 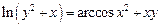 .
.
2.20 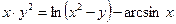 .
.
2.21 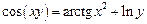 .
.
2.22 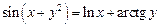 .
.
2.23 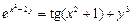 .
.
2.24 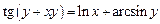 .
.
2.25 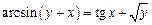 .
.
2.26 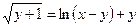 .
.
2.27 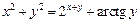 .
.
2.28 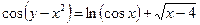 .
.
2.29 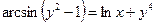 .
.
2.30 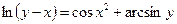 .
.
3 Найти производную функции с помощью логарифмической производной:
3.1 а) 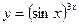 , б)
, б) 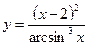 .
.
3.2 а) 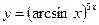 , б)
, б) 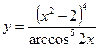 .
.
3.3 а) 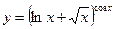 , б)
, б) 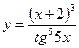 .
.
3.4 а) 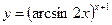 , б)
, б) 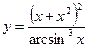 .
.
3.5 а) 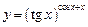 , б)
, б) 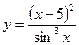 .
.
3.6 а) 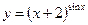 , б)
, б) 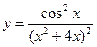 .
.
3.7 а) 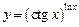 , б)
, б) 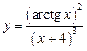 .
.
3.8а) 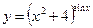 , б)
, б) 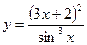 .
.
3.9 а) 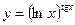 , б)
, б) 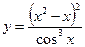 .
.
3.10 а) 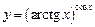 , б)
, б) 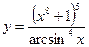 .
.
3.11 а) 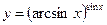 , б)
, б) 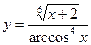 .
.
3.12а) 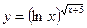 , б)
, б) 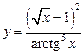 .
.
3.13 а) 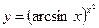 , б)
, б) 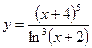 .
.
3.14 а) 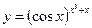 , б)
, б) 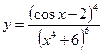 .
.
3.15 а) 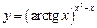 , б)
, б) 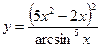 .
.
3.16 а) 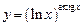 , б)
, б) 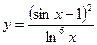 .
.
3.17 а) 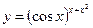 , б)
, б) 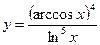 .
.
3.18 а) 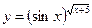 , б)
, б) 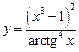 .
.
3.19 а) 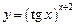 , б)
, б) 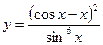 .
.
3.20 а) 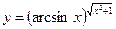 , б)
, б) 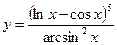 .
.
3.21 а) 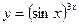 , б)
, б) 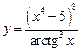 .
.
3.22 а) 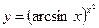 , б)
, б) 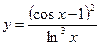 .
.
3.23 а) 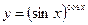 , б)
, б) 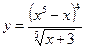 .
.
3.24 а) 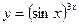 , б)
, б) 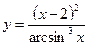 .
.
3.25 а) 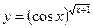 , б)
, б) 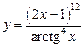 .
.
3.26 а) 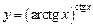 , б)
, б) 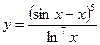 .
.
3.27 а) 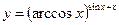 , б)
, б) 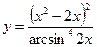 .
.
3.28 а) 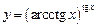 , б)
, б) 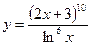 .
.
3.29 а) 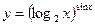 , б)
, б) 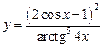 .
.
3.30 а) 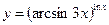 , б)
, б) 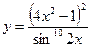 .
.
4 Найти производную 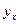 , функции
, функции 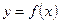 заданной параметрическими уравнениями:
заданной параметрическими уравнениями:
4.1 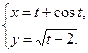 4.2
4.2 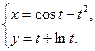
4.3 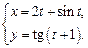 4.4
4.4 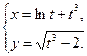
4.5 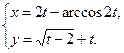 4.6
4.6 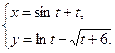
4.7 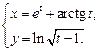 4.8
4.8 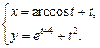
4.9 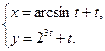 4.10
4.10 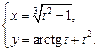
4.11 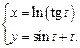 4.12
4.12 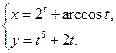
4.13 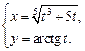 4.14
4.14 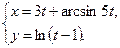
4.15 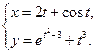 4.16
4.16 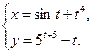
4.17 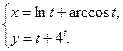 4.18
4.18 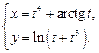
4.19 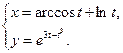 4.20
4.20 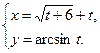
4.21 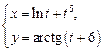 4.22
4.22 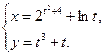
4.23 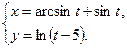 4.24
4.24 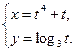
4.25 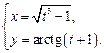 4.26
4.26 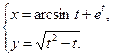
4.27 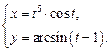 4.28
4.28 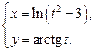
4.29 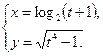 4.30
4.30 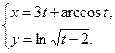
5. Найти дифференциал 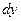 функции
функции 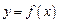 :
:
5.1 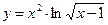 . 5.2
. 5.2 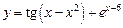 .
.
5.3 .5.4. .
5.5 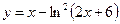 .5.6
.5.6 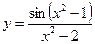 .
.
5.7 . 5.8. .
5.9 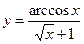 .5.10
.5.10 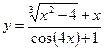 .
.
5.11 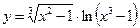 .5.12
.5.12 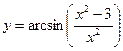 .
.
5.13 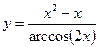 .5.14
.5.14 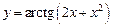 .
.
5.15 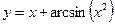 .5.16
.5.16 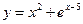 .
.
5.17 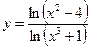 .5.18
.5.18 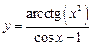 .
.
5.19 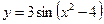 .5.20
.5.20 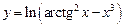 .
.
5.21 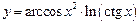 . 5.22
. 5.22 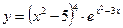 .
.
5.23 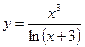 . 5.24
. 5.24 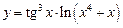 .
.
5.25 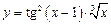 . 5.26
. 5.26 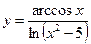 .
.
5.27 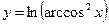 . 5.28
. 5.28 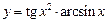 .
.
5.29 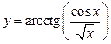 .5.30
.5.30 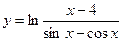 .
.
ИДЗ–2 Производные и дифференциалы высших порядков
1 Вычислить значение второй производной функции 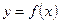 в точке
в точке 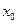 .
.
1.1 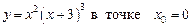 .
.
1.2 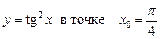 .
.
1.3 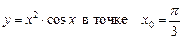 .
.
1.4 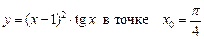 .
.
1.5 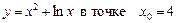 .
.
1.6 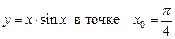 .
.
1.7 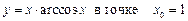 .
.
1.8 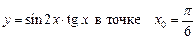 .
.
1.9 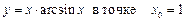 .
.
1.10 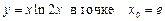 .
.
1.11 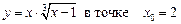 .
.
1.12 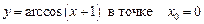 .
.
1.13 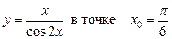 .
.
1.14 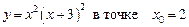 .
.
1.15 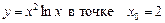 .
.
1.16 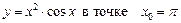 .
.
1.17 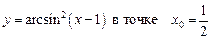 .
.
1.18 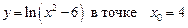 .
.
1.19 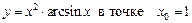 .
.
1.20. 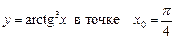 .
.
1.21 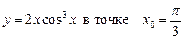 .
.
1.22 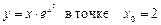 .
.
1.23 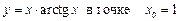 .
.
1.24 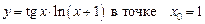 .
.
1.25 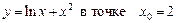 .
.
1.26 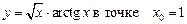 .
.
1.27 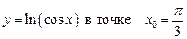 .
.
1.28 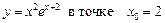 .
.
1.29 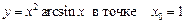 .
.
1.30 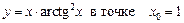 .
.
2 Разложить функцию 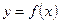 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 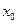 :
:
2.1 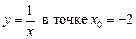 .2.2
.2.2 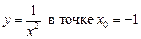 .
.
2.3 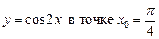 .2.4
.2.4 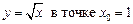 .
.
2.5 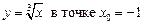 .2.6
.2.6 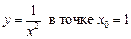 .
.
2.7 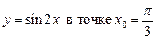 .2.8
.2.8 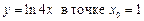 .
.
2.9 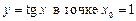 .2.10
.2.10 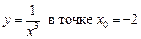 .
.
2.11 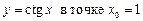 .2.12
.2.12 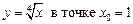 .
.
2.13 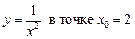 .2.14
.2.14 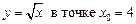 .
.
2.15 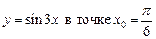 .2.16
.2.16 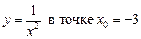 .
.
2.17 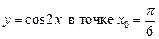 .2.18
.2.18 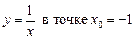 .
.
2.19 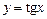 в точке
в точке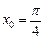 .2.20
.2.20 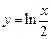 в точке
в точке 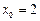 .
.
2.21 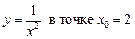 .2.22
.2.22 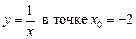 .
.
2.23 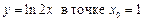 .2.24
.2.24 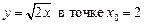 .
.
2.25 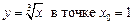 .2.26
.2.26 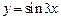 в точке
в точке 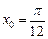 .
.
2.27 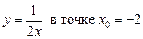 .2.28.
.2.28. 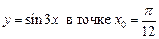 .
.
2.29 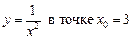 .2.30
.2.30 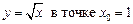 .
.
3 Написать разложение функции 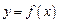 в ряд Маклорена по степеням переменной
в ряд Маклорена по степеням переменной 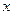 до членов порядка
до членов порядка 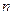 включительно:
включительно:
3.1 
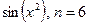 .3.2
.3.2 
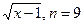 .
.
3.3 
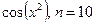 3.4
3.4 
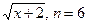 .
.
3.5 
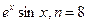 . 3.6
. 3.6 
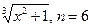 .
.
3.7 
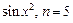 . 3.8
. 3.8 
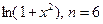 .
.
3.9 
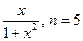 . 3.10
. 3.10 
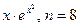 .
.
3.11 
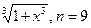 . 3.12
. 3.12 
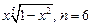 .
.
3.13 
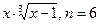 . 3.14
. 3.14 
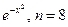 .
.
3.15 
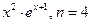 . 3.16
. 3.16 
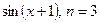 .
.
3.17 
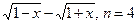 . 3.18
. 3.18 
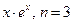 .
.
3.19 
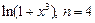 . 3.20
. 3.20 
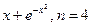 .
.
3.21 
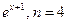 . 3.22
. 3.22 
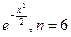 .
.
3.23 
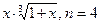 . 3.24
. 3.24 
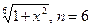 .
.
3.25 
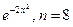 . 3.26
. 3.26 
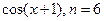 .
.
3.27 
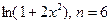 . 3.28
. 3.28 
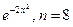 .
.
3.29 
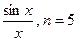 . 3.30
. 3.30 
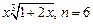 .
.
4 Используя правило Лопиталя, вычислить пределы:
4.1 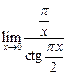 . 4.2
. 4.2 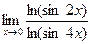 .
.
4.3 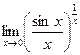 . 4.4
. 4.4 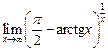
4.5 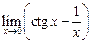 .4.6
.4.6 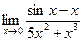 .
.
4.7 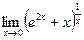 . 4.8
. 4.8 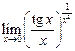 .
.
4.9 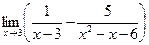 . 4.10
. 4.10 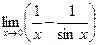 .
.
4.11 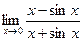 .4.12
.4.12 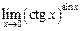 .
.
4.13 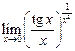 4.14
4.14 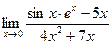
4.15 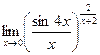 4.16
4.16 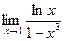 .
.
4.17 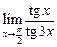 . 4.18
. 4.18 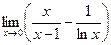 .
.
4.19 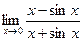 . 4.20
. 4.20 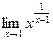 .
.
4.21 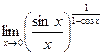 4.22
4.22 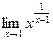 .
.
4.23 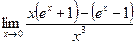 . 4.24
. 4.24 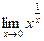 .
.
4.25 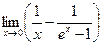 . 4.26
. 4.26 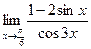 .
.
4.27 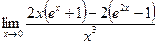 . 4.28
. 4.28 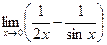 .
.
4.29 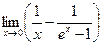 . 4.30
. 4.30 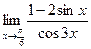 .
.
5 Вычислить приближенно значение функции 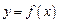 в точке
в точке 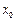 с помощью дифференциала:
с помощью дифференциала:
5.1 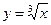 ,
,  7,76.
7,76.
5.2 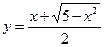 ,
,  0.98.
0.98.
5.3 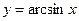 ,
,  0,08.
0,08.
5.4 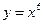 ,
,  2,01.
2,01.
5.5 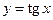 ,
, 
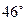 .
.
5.6 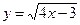 ,
,  1,08.
1,08.
5.7 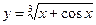 ,
,  0,01.
0,01.
5.8 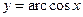 ,
,  0,48.
0,48.
5.9 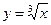 ,
,  1,03.
1,03.
5.10 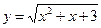 ,
,  1,95.
1,95.
5.11 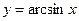 ,
,  0,51.
0,51.
5.12 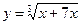 ,
,  1,012.
1,012.
5.13 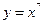 ,
,  2,002.
2,002.
5.14 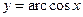 ,
,  0,52.
0,52.
5.15 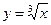 ,
,  8,24.
8,24.
5.16 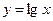 ,
,  10,02.
10,02.
5.17 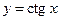 ,
, 
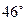 .
.
5.18 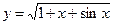 ,
,  0,01.
0,01.
5.19 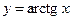 ,
,  0,98.
0,98.
5.20 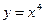 ,
,  3,998.
3,998.
5.21 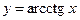 ,
,  1,04
1,04
5.22 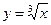 ,
,  1,21.
1,21.
5.23 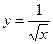 ,
,  4,16.
4,16.
5.24 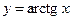 ,
,  1,02.
1,02.
5.25 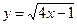 ,
,  2,56.
2,56.
5.26 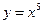 ,
,  2,995.
2,995.
5.27 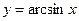 ,
,  0,09
0,09
5.28 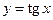 ,
, 
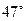 .
.
5.29 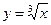 ,
,  7,64.
7,64.
5.30 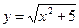 ,
,  1,95.
1,95.
ИДЗ – 3 Приложения производной
1Найти глобальный экстремум функции 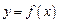 на отрезке
на отрезке 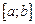 .
.
1.1 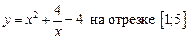 .
.
1.2 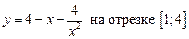 .
.
1.3 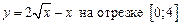 .
.
1.4 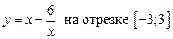 .
.
1.5 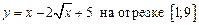 .
.
1.6 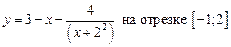 .
.
1.7 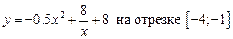 .
.
1.8 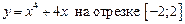 .
.
1.9 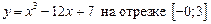 .
.
1.10 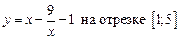 .
.
1.11 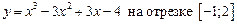 .
.
1.12 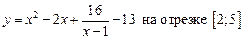 .
.
1.13 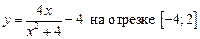 .
.
1.14 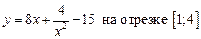 .
.
1.15 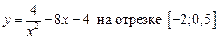 .
.
1.16 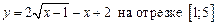 .
.
1.17 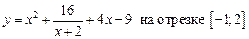 .
.
1.18 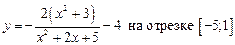 .
.
1.19 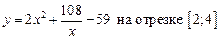 .
.
1.20 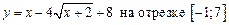 .
.
1.21 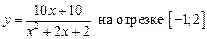 .
.
1.22 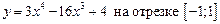 .
.
1.23 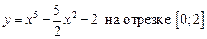 .
.
1.24 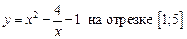 .
.
1.25 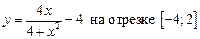 .
.
1.26 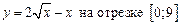 .
.
1.27 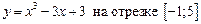 .
.
1.28 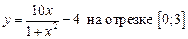 .
.
1.29 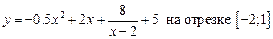 .
.
1.30 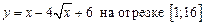 .
.
2 Решить геометрические задачи:
2.1 Найдите прямоугольный треугольник наибольшей площади, если сумма катета и гипотенузы его постоянна.
2.2 При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность?
2.3 В данный круговой сегмент, не превышающий полукруга, вписать прямоугольник наибольшей площади.
2.4 В эллипс 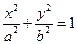 вписать прямоугольник со сторонами, параллельными осям эллипса, площадь которого наибольшая.
вписать прямоугольник со сторонами, параллельными осям эллипса, площадь которого наибольшая.
2.5 Боковое ребро правильной треугольной пирамиды имеет постоянную заданную длину и составляет с плоскостью основания угол 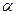 . При каком значении
. При каком значении 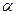 объём пирамиды является наибольшим?
объём пирамиды является наибольшим?
2.6 В полушар радиуса R вписать прямоугольный параллелепипед с квадратным основанием наибольшего объёма.
2.7 В данный шар радиуса R вписать цилиндр наибольшего объёма.
2.8 В шар радиусом R вписать цилиндр с наибольшей полной поверхностью.
2.9 Около шара радиуса r описать конус наименьшего объёма.
2.10 Через вершину М квадрата CEMK провести прямую, пересекающую лучи CK и CE в точках A и B так, чтобы площадь DABC была наименьшей.
2.11 Две стороны параллелограмма лежат на сторонах данного треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма является наибольшей?
2.12 Найти наибольший объём конуса с образующей l.
2.13 В прямой круговой конус с углом 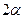 в осевом сечении и радиусом основания R вписать цилиндр с наибольшей полной поверхностью.
в осевом сечении и радиусом основания R вписать цилиндр с наибольшей полной поверхностью.
2.14 Найти кратчайшее расстояние точки M(p,p) от параболы 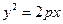 .
.
2.15 Найти наибольшую хорду эллипса 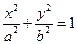 ,
, 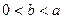 , проходящую через вершину
, проходящую через вершину 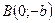 .
.
2.16 Через точку эллипса 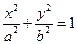 провести касательную, образующую с осями координат треугольник наименьшей площади.
провести касательную, образующую с осями координат треугольник наименьшей площади.
2.17 Найти основания и высоту равнобочной трапеции, которая при данной площади S имеет наименьший периметр; угол при большем основании трапеции равен 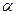 .
.
2.18 Какова должна быть высота равнобедренного треугольника, вписанного в окружность диаметра d, чтобы площадь треугольника была наибольшей?
2.19 В прямоугольный треугольник с гипотенузой 10 см и углом 30° вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы площадь его была наибольшей?
2.20 Требуется огородить забором прямоугольный участок земли площадью в 294 м2 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора окажется наименьшей?
2.21 Прямоугольный лист жести имеет линейные размеры 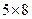 дм. В четырех его углах вырезают одинаковые квадраты и делают открытую коробку, загибая края под прямым углом. Какова наибольшая вместимость полученной коробки?
дм. В четырех его углах вырезают одинаковые квадраты и делают открытую коробку, загибая края под прямым углом. Какова наибольшая вместимость полученной коробки?
2.22 В прямоугольный треугольник с гипотенузой 24 см и углом 60° вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей?
2.23 Две стороны параллелограмма лежат на сторонах данного треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма является наибольшей?
2.24 Среди равнобедренных треугольников с данной боковой стороной 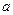 найти треугольник наибольшей площади.
найти треугольник наибольшей площади.
2.25 Боковые стороны и меньшее основание трапеции имеют одинаковые длины по 10 см. Найти размер большего основания, при котором площадь трапеции была бы наибольшей.
2.26 Найти длины сторон прямоугольника наибольшей площади, вписанного в прямоугольный треугольник со сторонами 18, 24 и 30 см и имеющего с ним общий прямой угол.
2.27 Величина угла при основании равнобедренного треугольника равна 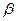 . При каком значении
. При каком значении 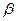 отношение длин радиусов вписанной и описанной окружностей является наибольшим?
отношение длин радиусов вписанной и описанной окружностей является наибольшим?
2.28 Каким должен быть радиус основания и высота цилиндрического бака, чтобы при данном объеме 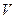 на его изготовление пошло наименьшее количество листового металла?
на его изготовление пошло наименьшее количество листового металла?
2.29 В прямоугольный треугольник с гипотенузой 12 см и углом 60° вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы площадь его была наибольшей?
2.30 Боковые стороны и меньшее основание трапеции имеют одинаковые длины по 15 см. Найти размер меньшего основания, при котором площадь трапеции была бы наибольшей.
3Решить физические задачи:
3.1 Тяжелую балку длиной 13 м, расположенную вертикально, опускают на землю так, что нижний её конец прикреплен к вагонетке, а верхний удерживается канатом, намотанным на ворот. Канат сматывается со скоростью 2 м/мин. С каким ускорением откатывается вагонетка в момент, когда она npoйдёт расстояние 5 м?
3.2 Антенна радара находится на расстоянии 1000 м по горизонтали от стартовой площадки и все время направлена на ракету, которая поднимается с постоянным ускорением 20 м/с2. Какова угловая скорость антенны в момент, когда ракета находится не высоте 1000 м?
3.3 Лошадь бежит по окружности со скоростью 20 м/с. В центре окружности находится фонарь. Забор касается окружности в точке, из которой лошадь начинает бег. С какой скоростью перемешается тень лошади вдоль забора в момент, когда лошадь пробежит 1/8 окружности?
3.4 Резервуар, имеющий форму полушара радиуса 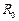 , заполняется водой. Скорость заполнения резервуара равна
, заполняется водой. Скорость заполнения резервуара равна 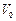 . Определите скорость подъёма воды в резервуаре в момент, когда вода поднялась на высоту
. Определите скорость подъёма воды в резервуаре в момент, когда вода поднялась на высоту 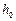 .
.
3.5 Длина вертикально стоящей лестницы равна 5 м. Нижний конец лестницы начинает отодвигаться от стены с постоянной скоростью 2 м/с. Чему равно ускорение верхнего конца лестницы в момент, когда нижний конец отодвинулся от стены на 1 м?
3.6Канат висячего моста, имеющего форму цепной линии, т. е. графика функции 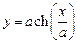 , прикреплен к вертикальным опорам, отстоящим друг от друга на расстоянии 200 м. Самая нижняя точка каната находится на 40 м ниже точки подвеса. Чему равен угол между канатом и опорой в точке подвеса (для определения a можно воспользоваться равенством
, прикреплен к вертикальным опорам, отстоящим друг от друга на расстоянии 200 м. Самая нижняя точка каната находится на 40 м ниже точки подвеса. Чему равен угол между канатом и опорой в точке подвеса (для определения a можно воспользоваться равенством 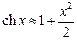 )?
)?
3.7 В точках A и B находятся источники света силы 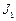 и
и 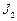 соответственно,
соответственно, 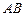
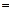 27. Найдите на отрезке
27. Найдите на отрезке 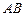 наименее освещенную точку (освещенность прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния до него).
наименее освещенную точку (освещенность прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния до него).
3.8 Бревно длиной 10 м с помощью подъёмного крана поднимается вертикально вверх за один из его концов. При этом второй конец волочится по земле со скоростью 0,05 м/с. С какой скоростью перемещается верхний конец бревна в момент, когда его нижний конец находится на расстоянии 3 м от вертикали?
3.9 Мальчик надувает воздушный шар, радиус которого возрастает с постоянным ускорением 0,2 см/с2. С какой скоростью увеличивается объём шара в момент, когда площадь его поверхности равна 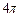 см2 (радиус шара в начальный момент времени равнялся нулю)?
см2 (радиус шара в начальный момент времени равнялся нулю)?
3.10 Человек, рост которого 1,7 м, удаляется от точечного источника света, расположенного на высоте 3 м, с постоянным ускорением 0,1 м/с2. С каким ускорением перемещается тень его головы?
3.11 Скорость тела, движущегося по окружности радиуса 1 м, меняется по закону 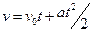 . Найдите величину ускорения тела в момент времени
. Найдите величину ускорения тела в момент времени 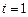 c.
c.
3.12 Зависимость пути, пройденного телом, движущимся по окружности радиуса 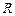 , от времени задается уравнением
, от времени задается уравнением 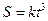 (
( 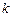
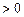 ). Чему равна величина скорости тела в момент, когда оно пройдёт путь
). Чему равна величина скорости тела в момент, когда оно пройдёт путь 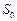 ?
?
3.13 Частица движется с постоянной по величине скоростью 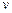 по кривой
по кривой 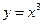 . Найдите величину ускорения частицы в момент, когда
. Найдите величину ускорения частицы в момент, когда 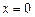 .
.
