Вычисление интегралов Стилтьеса
 Если функция
Если функция 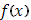 интегрируема в смысле Римана в промежутке
интегрируема в смысле Римана в промежутке 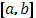 , а
, а  представлена интегралом
представлена интегралом
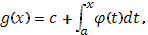
где функция 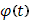 абсолютн
абсолютн  интегрируема в
интегрируема в 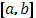 , то
, то
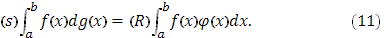
Интеграл справа существует. Существование Стилтьеса было уже доказано в п.3 (III). Остается лишь установить равенство (11).
Предположим, что 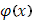 - положительная функция (для упрощения).
- положительная функция (для упрощения).
Составим сумму Стилтьеса
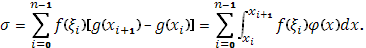
Так как, с другой стороны, можно написать
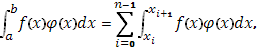
то будем иметь
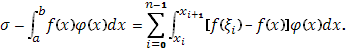
Очевидно, для 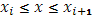 будет
будет 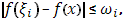 где
где 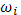 - это колебание функции
- это колебание функции 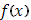 в промежутке
в промежутке 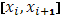 . Отсюда выкает оценка написанной выше разности:
. Отсюда выкает оценка написанной выше разности:
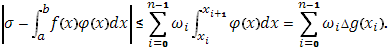
Т.к. в п.3 (III) мы доказали, что при 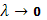
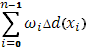 стремится к 0, следовательно
стремится к 0, следовательно
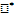 Если с интегралом
Если с интегралом 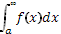 сходится и интеграл
сходится и интеграл 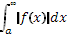 , то интеграл
, то интеграл 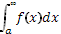 называют абсолютно сходящимся, а функцию fix
называют абсолютно сходящимся, а функцию fix
) - аб
солютно интегрируемой в промежутке [а, + 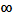 ]
]
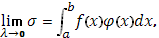
что и доказывает формулу (11).
 При прежних предложениях относительно функции
При прежних предложениях относительно функции 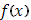 допустим, что функция
допустим, что функция  непрерывна во всем промежутке
непрерывна во всем промежутке 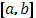 и имеем, исключая разве лишь конечное число точек, производную
и имеем, исключая разве лишь конечное число точек, производную 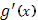 , которая в
, которая в 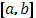 абсолютно интегрируема. Тогда
абсолютно интегрируема. Тогда
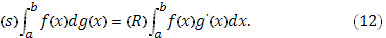
Интеграл справа в формуле (12) формально получается из интеграла слева, если, понимая символ 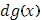 буквально как дифференциал, заменить его выражением
буквально как дифференциал, заменить его выражением 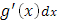 .
.
Если функция  оказывается разрывной, то начнем с рассмотрения «стандартной» разрывной функции
оказывается разрывной, то начнем с рассмотрения «стандартной» разрывной функции 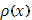 , определяемой равенствами
, определяемой равенствами
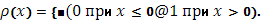
Она имеет разрыв первого рода - скачок - в точке x=0 справа, причем величина скачка 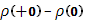 равна 1; в точке x=0 слева и в остальных точках функции
равна 1; в точке x=0 слева и в остальных точках функции 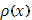 непрерывна. Функция
непрерывна. Функция 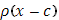 будет иметь такой же разрыв в точке x=c справа; наоборот,
будет иметь такой же разрыв в точке x=c справа; наоборот, 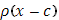 будет иметь подобный разрыв в точке x=c слева, причем величина скачка будет равна -1.
будет иметь подобный разрыв в точке x=c слева, причем величина скачка будет равна -1.
Предположим, что функция 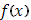 непрерывна в точке x=c, и вычислим интеграл
непрерывна в точке x=c, и вычислим интеграл
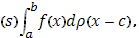
где 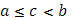 при (c=b этот интеграл равен нулю).
при (c=b этот интеграл равен нулю).
Составим сумму Стилтьеса:
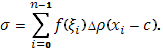
Пусть точка c попадет в k-й промежуток, так что 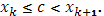 Тогда
Тогда 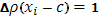 , а при
, а при 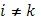
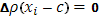 . Таким образом, вся сумма
. Таким образом, вся сумма 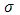 сводится к одному слагаемому:
сводится к одному слагаемому: 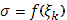 . Пусть теперь
. Пусть теперь 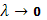 . По непрерывности
. По непрерывности 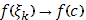 . Следовательно, существует (при
. Следовательно, существует (при 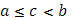 )
)
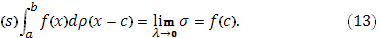
Аналогично можно убедиться в том, что (при 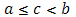 )
)
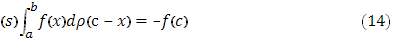
(при c=a этот интеграл обращается в нуль).
Пусть функция 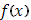 в промежутке
в промежутке 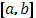 непрерывна, а
непрерывна, а  имеет в этом промежутке, исключая разве лишь конечное число точек, производную
имеет в этом промежутке, исключая разве лишь конечное число точек, производную 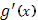 , которая абсолютно интегрируема в
, которая абсолютно интегрируема в 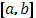 . При этом пусть функция
. При этом пусть функция  в конечном числе точек
в конечном числе точек
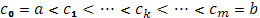
Терпит разрыв первого рода. Тогда существует интеграл Стилтьеса и выражается формулой
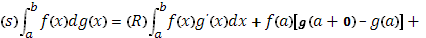
Характерно здесь наличие внеинтегральной суммы, где фигурируют скачки функции  в точках a
в точках a
или b – односторонние (если на деле какой-либо из этих точек скачка нет, то соответствующее слагаемое суммы обращается в нуль).
Для упрощения записи введем обозначения для скачков функции  справа и слева:
справа и слева:
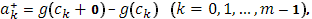
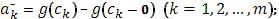
очевидно, для 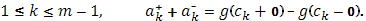
Составим вспомогательную функцию:
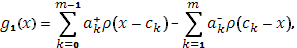
которая как бы вбирает в себя все разрывы функции  , так что разность
, так что разность 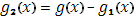 оказывается непрерывной (по доказанному ранее).
оказывается непрерывной (по доказанному ранее).
Для значений 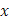 , отличных от всех
, отличных от всех 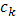 , непрерывность функции
, непрерывность функции 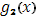 не вызывает сомнений, т.к. для этих значений непрерывны обе функции
не вызывает сомнений, т.к. для этих значений непрерывны обе функции  и
и 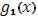 . Докажем непрерывность
. Докажем непрерывность 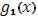 в точке
в точке 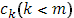 справа. Все слагаемые суммы
справа. Все слагаемые суммы 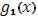 , кроме члена
, кроме члена 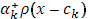 , непрерывны при
, непрерывны при 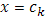 справа; поэтому достаточно изучить поведение выражения
справа; поэтому достаточно изучить поведение выражения 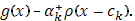 При
При 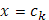 оно имеет значение
оно имеет значение 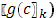 ; но таков же и предел при
; но таков же и предел при 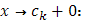
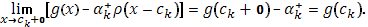
Аналогично проверяется и непрерывность функции  в точке
в точке  слева.
слева.
Далее, если взять точку 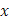 (отличную от всех
(отличную от всех 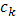 ), в которой функция
), в которой функция  имеет производную, то вблизи этой точки
имеет производную, то вблизи этой точки 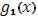 сохраняет постоянное значение, следовательно, в ней и функция
сохраняет постоянное значение, следовательно, в ней и функция 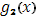 имеет производную, причем
имеет производную, причем 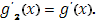
Для непрерывности функции 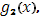 по предыдущей теореме, существует интеграл Стилтьеса
по предыдущей теореме, существует интеграл Стилтьеса
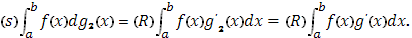
Точно так же легко вычислить и интеграл (с учетом (13), (14))
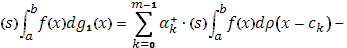
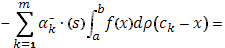

Складывая почленно эти два равенства, придем к равенству (15); существование интеграла Стилтьеса от 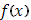 по функции
по функции
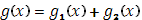 устанавливается попутно свойство
устанавливается попутно свойство  в п.4.
в п.4.
продолжение
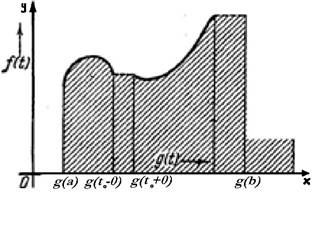
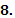 Геометрическая иллюстрация интеграла Стилтьеса.
Геометрическая иллюстрация интеграла Стилтьеса.
Рассмотрим интеграл

предполагая функцию 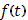 непрерывной и положительной а
непрерывной и положительной а 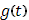 -монотонно возрастающей (в строгом смысле); функция
-монотонно возрастающей (в строгом смысле); функция 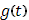 может иметь и разрывы (скачки).
может иметь и разрывы (скачки).
Система параметрических уравнений 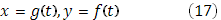
выражает некоторую кривую (K) , разрывную, как на рисунке.
 Если при некотором
Если при некотором 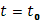 функция
функция 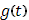 испытывает скачок, так что
испытывает скачок, так что 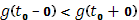 , то этим предельным значениям
, то этим предельным значениям 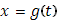 отвечает одно и то же предельное значение
отвечает одно и то же предельное значение 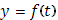 , равное
, равное 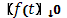 ). Дополним кривую (K) всем горизонтальным отрезками, соединяющими пары точек
). Дополним кривую (K) всем горизонтальным отрезками, соединяющими пары точек
отвечающие всем скачкам функции 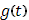 (по рисунку). Таким образом, составится уже непрерывная кривая (L). Покажем, что интеграл (16) представляет площадь фигуры под этой кривой, т.е. площадь фигуры, ограниченной кривой (L), осью x и двумя крайними ординатами, отвечающими абсциссам
(по рисунку). Таким образом, составится уже непрерывная кривая (L). Покажем, что интеграл (16) представляет площадь фигуры под этой кривой, т.е. площадь фигуры, ограниченной кривой (L), осью x и двумя крайними ординатами, отвечающими абсциссам 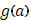 и
и 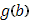 .
.
С этой целью разложим промежуток 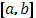 на части точками
на части точками
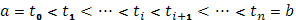
и в соответствии с этим промежуток 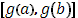 на оси
на оси 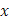 - на части точками
- на части точками
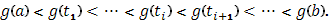
Введя наименьшее и наибольшее значения 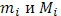 функции
функции 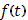 в i-ом промежутке
в i-ом промежутке 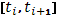 , составим нижнюю и верхнюю суммы Стилтьеса – Дарбу
, составим нижнюю и верхнюю суммы Стилтьеса – Дарбу
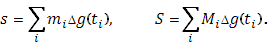
Они представляют площади фигур, составленных из входящих и из выходящих прямоугольников, между которыми содержится рассматриваемая криволинейная фигура.
Так как при стремлении в 0 всех 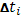 обе суммы стремятся к общему пределу (16), то отсюда следует, что фигура, изображенная на рисунке квадрируема и площадью ее служит действительно интеграл (16).
обе суммы стремятся к общему пределу (16), то отсюда следует, что фигура, изображенная на рисунке квадрируема и площадью ее служит действительно интеграл (16).
 Теорема о среднем, оценки.
Теорема о среднем, оценки.
 Пусть в промежутке
Пусть в промежутке 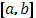 функция
функция 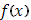 ограничена:
ограничена: 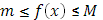 , а
, а  монотонно возрастает. Если существует интеграл Стилтьеса
монотонно возрастает. Если существует интеграл Стилтьеса 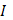 от
от 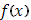 и
и  , то имеет место формула
, то имеет место формула
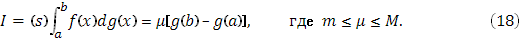
То есть это теорема о среднем для интегралов Стилтьеса.
Доказательство:
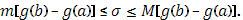
Переходя к пределу, получим

Возьмем 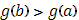 , т.к. случай
, т.к. случай 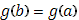 (т.е.
(т.е. 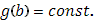 ) не представляет интереса: обе части формулы (18) – нули.
) не представляет интереса: обе части формулы (18) – нули.
Тогда
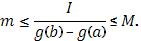
Обозначая написанное отношение через 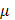 и придем к (18).
и придем к (18).
Если 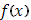 в промежутке
в промежутке 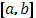 непрерывна, тогда
непрерывна, тогда 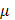 и есть значение функции в некоторой точке этого промежутка, и формула (18) имеет вид
и есть значение функции в некоторой точке этого промежутка, и формула (18) имеет вид
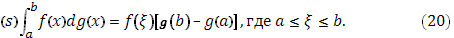
 Пусть
Пусть 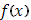 непрерывна, а функция
непрерывна, а функция  имеет ограниченное изменение. Для этого случая справедлива оценка интеграла Стилтьеса:
имеет ограниченное изменение. Для этого случая справедлива оценка интеграла Стилтьеса:

где 
Доказательство:
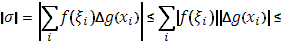
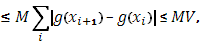
так что остается лишь перейти к пределу, чтобы получить (21).
 Пусть в промежутке
Пусть в промежутке 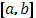 функция
функция 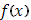 ограничена,
ограничена,  монотонно возрастает. Если существует интеграл Стилтьеса
монотонно возрастает. Если существует интеграл Стилтьеса 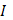 от
от 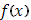 и
и  , то имеет место формула
, то имеет место формула
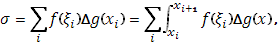
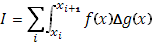
и почленно вычитая эти равенства, получим
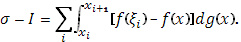
Обозначим через 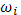 колебание функции
колебание функции 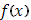 в промежутке
в промежутке 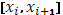 , тогда
, тогда
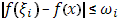 для
для 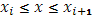 , то, применяя оценку (21) к каждому интегралу с границами
, то, применяя оценку (21) к каждому интегралу с границами 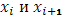 в отдельности, получаем:
в отдельности, получаем:
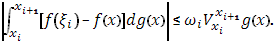
Если промежуток 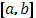 раздроблен на столь мелкие части, что все
раздроблен на столь мелкие части, что все 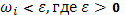 – произвольное наперед заданное взятое число, тогда
– произвольное наперед заданное взятое число, тогда

